An Adaptive Recursive Volatility Prediction Method

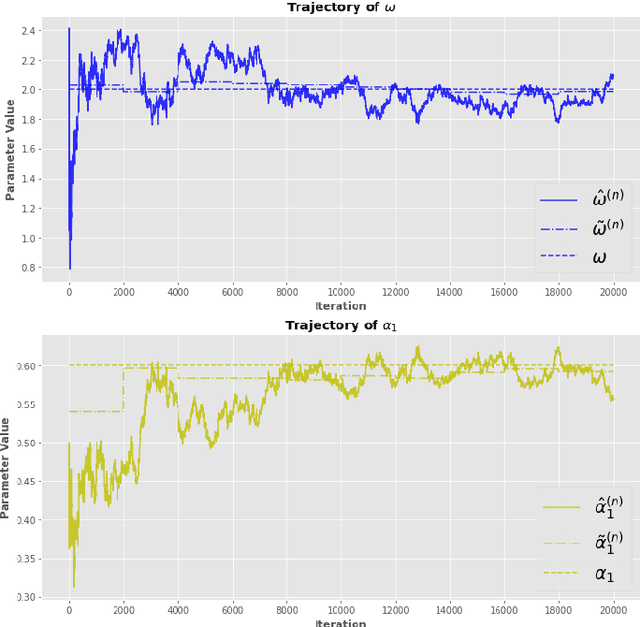
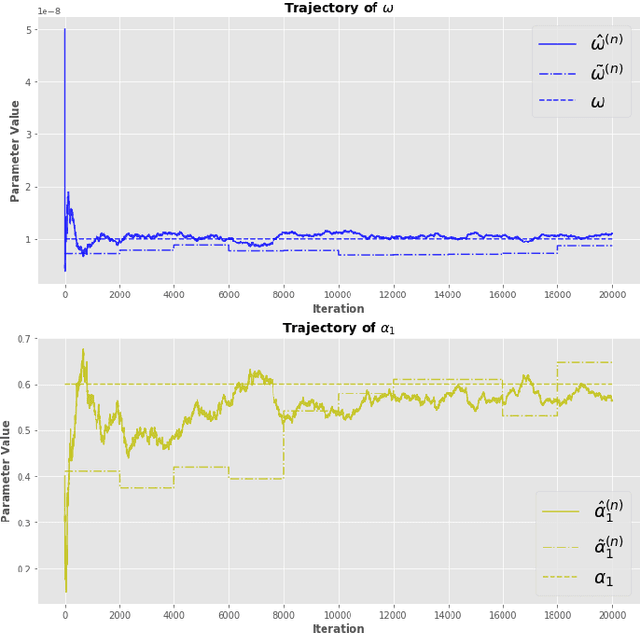
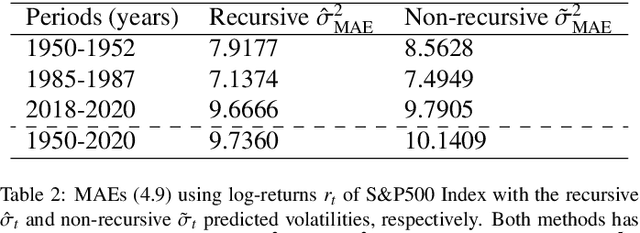
The Quasi-Maximum Likelihood (QML) procedure is widely used for statistical inference due to its robustness against overdisper-sion. However, while there are extensive references on non-recursive QML estimation, recursive QML estimation has attracted little attention until recently. In this paper, we investigate the convergence properties of the QML procedure in a general conditionally heteroscedastic time series model, extending the classical offline optimization routines to recursive approximation. We propose an adaptive recursive estimation routine for GARCH models using the technique of Variance Targeting Estimation (VTE) to alleviate the convergence difficulties encountered in the usual QML estimation. Finally, empirical results demonstrate a favorable trade-off between the ability to adapt to time-varying estimates and stability of the estimation routine.