Olivier Wintenberger
LPSM
Decreasing Entropic Regularization Averaged Gradient for Semi-Discrete Optimal Transport
Oct 31, 2025Abstract:Adding entropic regularization to Optimal Transport (OT) problems has become a standard approach for designing efficient and scalable solvers. However, regularization introduces a bias from the true solution. To mitigate this bias while still benefiting from the acceleration provided by regularization, a natural solver would adaptively decrease the regularization as it approaches the solution. Although some algorithms heuristically implement this idea, their theoretical guarantees and the extent of their acceleration compared to using a fixed regularization remain largely open. In the setting of semi-discrete OT, where the source measure is continuous and the target is discrete, we prove that decreasing the regularization can indeed accelerate convergence. To this end, we introduce DRAG: Decreasing (entropic) Regularization Averaged Gradient, a stochastic gradient descent algorithm where the regularization decreases with the number of optimization steps. We provide a theoretical analysis showing that DRAG benefits from decreasing regularization compared to a fixed scheme, achieving an unbiased $\mathcal{O}(1/t)$ sample and iteration complexity for both the OT cost and the potential estimation, and a $\mathcal{O}(1/\sqrt{t})$ rate for the OT map. Our theoretical findings are supported by numerical experiments that validate the effectiveness of DRAG and highlight its practical advantages.
Sliding-Window Signatures for Time Series: Application to Electricity Demand Forecasting
Oct 14, 2025

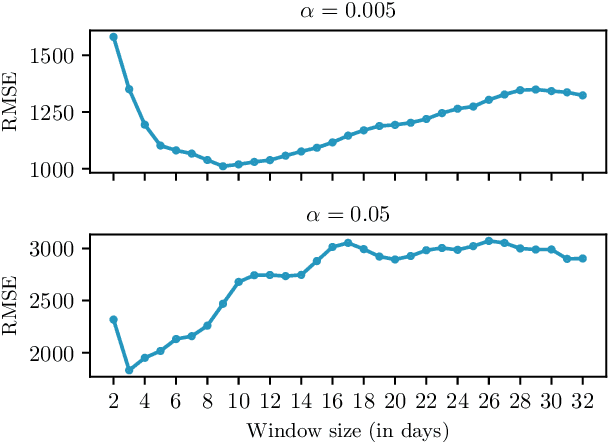
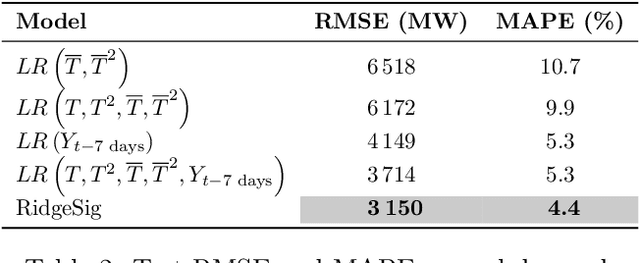
Abstract:Nonlinear and delayed effects of covariates often render time series forecasting challenging. To this end, we propose a novel forecasting framework based on ridge regression with signature features calculated on sliding windows. These features capture complex temporal dynamics without relying on learned or hand-crafted representations. Focusing on the discrete-time setting, we establish theoretical guarantees, namely universality of approximation and stationarity of signatures. We introduce an efficient sequential algorithm for computing signatures on sliding windows. The method is evaluated on both synthetic and real electricity demand data. Results show that signature features effectively encode temporal and nonlinear dependencies, yielding accurate forecasts competitive with those based on expert knowledge.
Asymptotic Normality of Infinite Centered Random Forests -Application to Imbalanced Classification
Jun 10, 2025
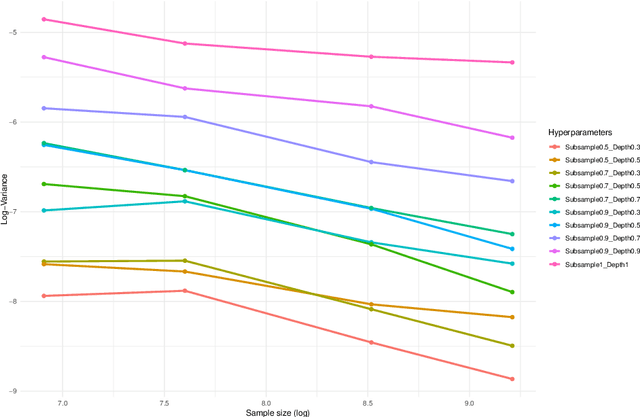
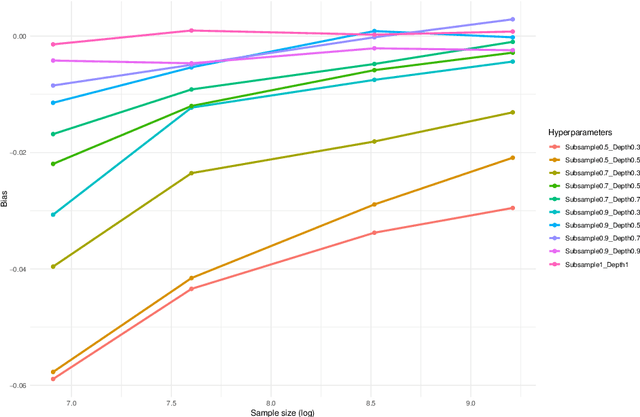
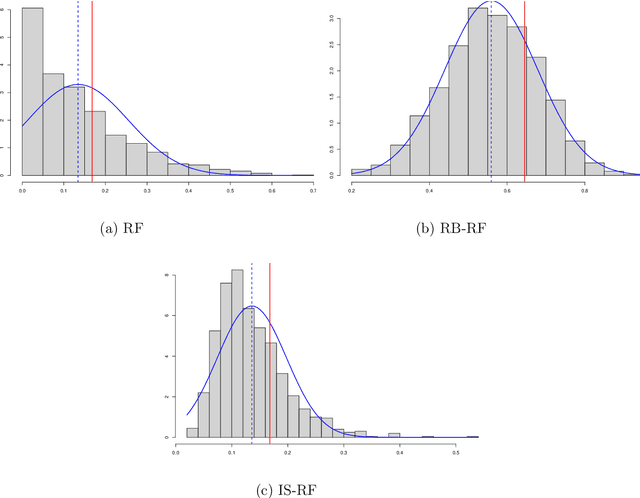
Abstract:Many classification tasks involve imbalanced data, in which a class is largely underrepresented. Several techniques consists in creating a rebalanced dataset on which a classifier is trained. In this paper, we study theoretically such a procedure, when the classifier is a Centered Random Forests (CRF). We establish a Central Limit Theorem (CLT) on the infinite CRF with explicit rates and exact constant. We then prove that the CRF trained on the rebalanced dataset exhibits a bias, which can be removed with appropriate techniques. Based on an importance sampling (IS) approach, the resulting debiased estimator, called IS-ICRF, satisfies a CLT centered at the prediction function value. For high imbalance settings, we prove that the IS-ICRF estimator enjoys a variance reduction compared to the ICRF trained on the original data. Therefore, our theoretical analysis highlights the benefits of training random forests on a rebalanced dataset (followed by a debiasing procedure) compared to using the original data. Our theoretical results, especially the variance rates and the variance reduction, appear to be valid for Breiman's random forests in our experiments.
Minimax Adaptive Online Nonparametric Regression over Besov Spaces
May 26, 2025Abstract:We study online adversarial regression with convex losses against a rich class of continuous yet highly irregular prediction rules, modeled by Besov spaces $B_{pq}^s$ with general parameters $1 \leq p,q \leq \infty$ and smoothness $s > d/p$. We introduce an adaptive wavelet-based algorithm that performs sequential prediction without prior knowledge of $(s,p,q)$, and establish minimax-optimal regret bounds against any comparator in $B_{pq}^s$. We further design a locally adaptive extension capable of dynamically tracking spatially inhomogeneous smoothness. This adaptive mechanism adjusts the resolution of the predictions over both time and space, yielding refined regret bounds in terms of local regularity. Consequently, in heterogeneous environments, our adaptive guarantees can significantly surpass those obtained by standard global methods.
Minimax Adaptive Boosting for Online Nonparametric Regression
Oct 04, 2024
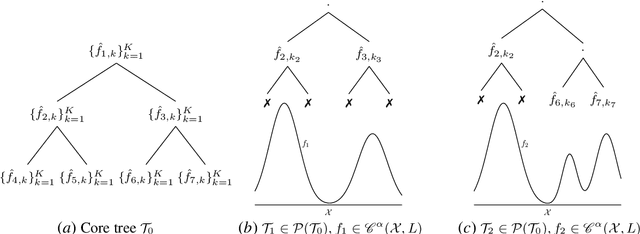
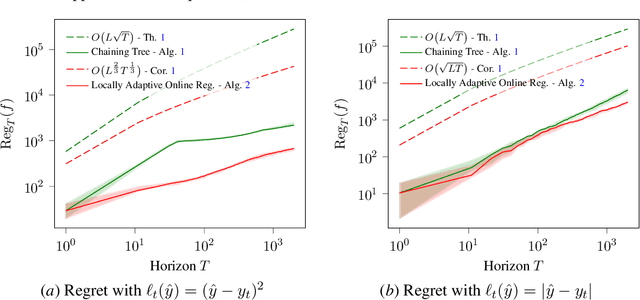
Abstract:We study boosting for adversarial online nonparametric regression with general convex losses. We first introduce a parameter-free online gradient boosting (OGB) algorithm and show that its application to chaining trees achieves minimax optimal regret when competing against Lipschitz functions. While competing with nonparametric function classes can be challenging, the latter often exhibit local patterns, such as local Lipschitzness, that online algorithms can exploit to improve performance. By applying OGB over a core tree based on chaining trees, our proposed method effectively competes against all prunings that align with different Lipschitz profiles and demonstrates optimal dependence on the local regularities. As a result, we obtain the first computationally efficient algorithm with locally adaptive optimal rates for online regression in an adversarial setting.
Semi-Discrete Optimal Transport: Nearly Minimax Estimation With Stochastic Gradient Descent and Adaptive Entropic Regularization
May 23, 2024Abstract:Optimal Transport (OT) based distances are powerful tools for machine learning to compare probability measures and manipulate them using OT maps. In this field, a setting of interest is semi-discrete OT, where the source measure $\mu$ is continuous, while the target $\nu$ is discrete. Recent works have shown that the minimax rate for the OT map is $\mathcal{O}(t^{-1/2})$ when using $t$ i.i.d. subsamples from each measure (two-sample setting). An open question is whether a better convergence rate can be achieved when the full information of the discrete measure $\nu$ is known (one-sample setting). In this work, we answer positively to this question by (i) proving an $\mathcal{O}(t^{-1})$ lower bound rate for the OT map, using the similarity between Laguerre cells estimation and density support estimation, and (ii) proposing a Stochastic Gradient Descent (SGD) algorithm with adaptive entropic regularization and averaging acceleration. To nearly achieve the desired fast rate, characteristic of non-regular parametric problems, we design an entropic regularization scheme decreasing with the number of samples. Another key step in our algorithm consists of using a projection step that permits to leverage the local strong convexity of the regularized OT problem. Our convergence analysis integrates online convex optimization and stochastic gradient techniques, complemented by the specificities of the OT semi-dual. Moreover, while being as computationally and memory efficient as vanilla SGD, our algorithm achieves the unusual fast rates of our theory in numerical experiments.
Online Learning Approach for Survival Analysis
Feb 07, 2024Abstract:We introduce an online mathematical framework for survival analysis, allowing real time adaptation to dynamic environments and censored data. This framework enables the estimation of event time distributions through an optimal second order online convex optimization algorithm-Online Newton Step (ONS). This approach, previously unexplored, presents substantial advantages, including explicit algorithms with non-asymptotic convergence guarantees. Moreover, we analyze the selection of ONS hyperparameters, which depends on the exp-concavity property and has a significant influence on the regret bound. We propose a stochastic approach that guarantees logarithmic stochastic regret for ONS. Additionally, we introduce an adaptive aggregation method that ensures robustness in hyperparameter selection while maintaining fast regret bounds. The findings of this paper can extend beyond the survival analysis field, and are relevant for any case characterized by poor exp-concavity and unstable ONS. Finally, these assertions are illustrated by simulation experiments.
Adaptive Probabilistic Forecasting of Electricity (Net-)Load
Jan 24, 2023Abstract:We focus on electricity load forecasting under three important specificities. First, our setting is adaptive; we use models taking into account the most recent observations available, yielding a forecasting strategy able to automatically respond to regime changes. Second, we consider probabilistic rather than point forecasting; indeed, uncertainty quantification is required to operate electricity systems efficiently and reliably. Third, we consider both conventional load (consumption only) and netload (consumption less embedded generation). Our methodology relies on the Kalman filter, previously used successfully for adaptive point load forecasting. The probabilistic forecasts are obtained by quantile regressions on the residuals of the point forecasting model. We achieve adaptive quantile regressions using the online gradient descent; we avoid the choice of the gradient step size considering multiple learning rates and aggregation of experts. We apply the method to two data sets: the regional net-load in Great Britain and the demand of seven large cities in the United States. Adaptive procedures improve forecast performance substantially in both use cases and for both point and probabilistic forecasting.
Optimistic Dynamic Regret Bounds
Jan 18, 2023Abstract:Online Learning (OL) algorithms have originally been developed to guarantee good performances when comparing their output to the best fixed strategy. The question of performance with respect to dynamic strategies remains an active research topic. We develop in this work dynamic adaptations of classical OL algorithms based on the use of experts' advice and the notion of optimism. We also propose a constructivist method to generate those advices and eventually provide both theoretical and experimental guarantees for our procedures.
Learning from time-dependent streaming data with online stochastic algorithms
May 25, 2022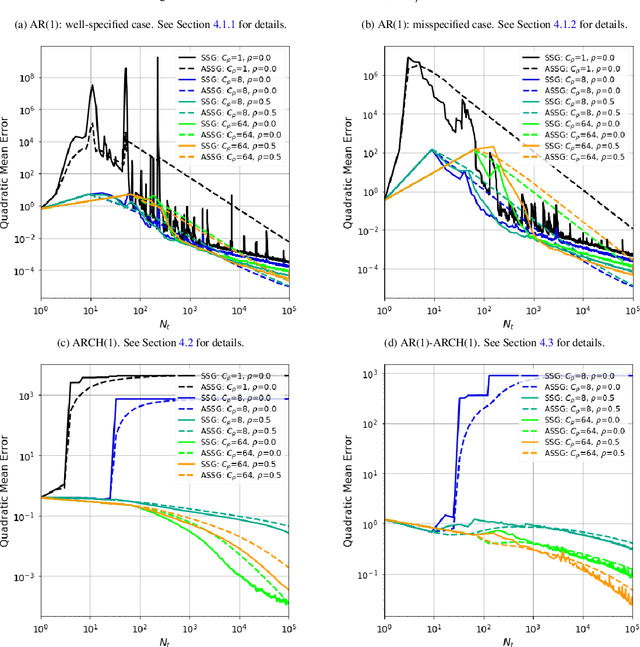
Abstract:We study stochastic algorithms in a streaming framework, trained on samples coming from a dependent data source. In this streaming framework, we analyze the convergence of Stochastic Gradient (SG) methods in a non-asymptotic manner; this includes various SG methods such as the well-known stochastic gradient descent (i.e., Robbins-Monro algorithm), mini-batch SG methods, together with their averaged estimates (i.e., Polyak-Ruppert averaged). Our results form a heuristic by linking the level of dependency and convexity to the rest of the model parameters. This heuristic provides new insights into choosing the optimal learning rate, which can help increase the stability of SGbased methods; these investigations suggest large streaming batches with slow decaying learning rates for highly dependent data sources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge