Joseph de Vilmarest
LPSM
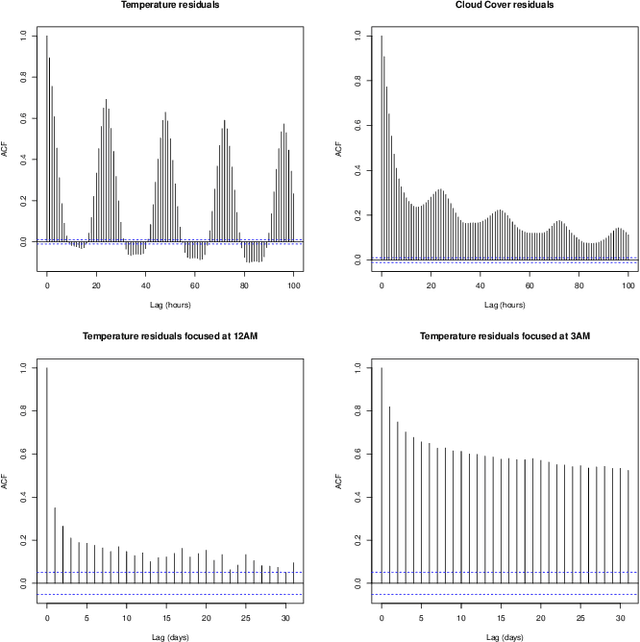
Sliding-Window Signatures for Time Series: Application to Electricity Demand Forecasting
Oct 14, 2025Abstract:Nonlinear and delayed effects of covariates often render time series forecasting challenging. To this end, we propose a novel forecasting framework based on ridge regression with signature features calculated on sliding windows. These features capture complex temporal dynamics without relying on learned or hand-crafted representations. Focusing on the discrete-time setting, we establish theoretical guarantees, namely universality of approximation and stationarity of signatures. We introduce an efficient sequential algorithm for computing signatures on sliding windows. The method is evaluated on both synthetic and real electricity demand data. Results show that signature features effectively encode temporal and nonlinear dependencies, yielding accurate forecasts competitive with those based on expert knowledge.
Adaptive time series forecasting with markovian variance switching
Feb 22, 2024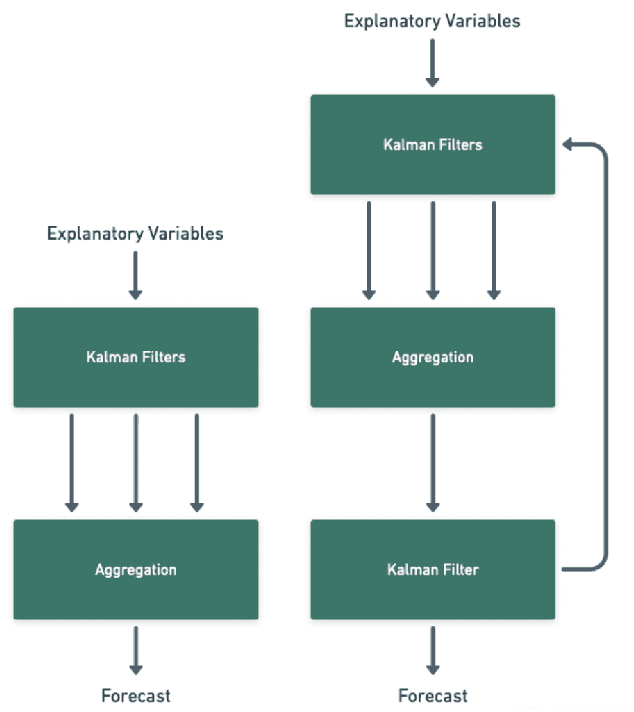
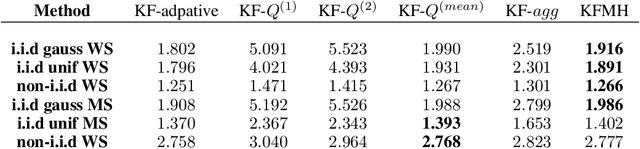
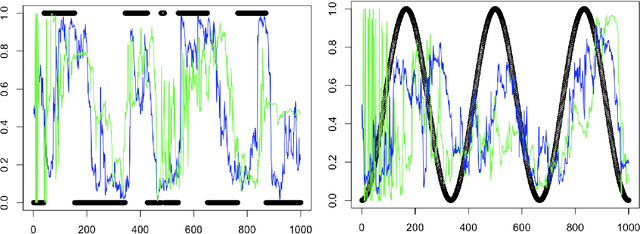
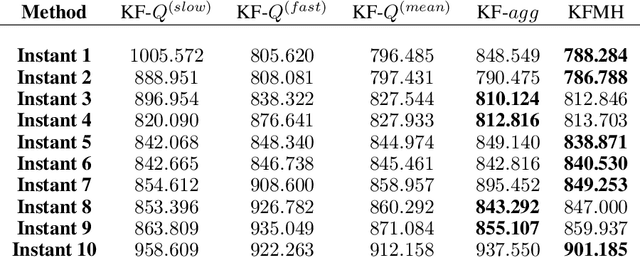
Abstract:Adaptive time series forecasting is essential for prediction under regime changes. Several classical methods assume linear Gaussian state space model (LGSSM) with variances constant in time. However, there are many real-world processes that cannot be captured by such models. We consider a state-space model with Markov switching variances. Such dynamical systems are usually intractable because of their computational complexity increasing exponentially with time; Variational Bayes (VB) techniques have been applied to this problem. In this paper, we propose a new way of estimating variances based on online learning theory; we adapt expert aggregation methods to learn the variances over time. We apply the proposed method to synthetic data and to the problem of electricity load forecasting. We show that this method is robust to misspecification and outperforms traditional expert aggregation.
Online Learning Approach for Survival Analysis
Feb 07, 2024Abstract:We introduce an online mathematical framework for survival analysis, allowing real time adaptation to dynamic environments and censored data. This framework enables the estimation of event time distributions through an optimal second order online convex optimization algorithm-Online Newton Step (ONS). This approach, previously unexplored, presents substantial advantages, including explicit algorithms with non-asymptotic convergence guarantees. Moreover, we analyze the selection of ONS hyperparameters, which depends on the exp-concavity property and has a significant influence on the regret bound. We propose a stochastic approach that guarantees logarithmic stochastic regret for ONS. Additionally, we introduce an adaptive aggregation method that ensures robustness in hyperparameter selection while maintaining fast regret bounds. The findings of this paper can extend beyond the survival analysis field, and are relevant for any case characterized by poor exp-concavity and unstable ONS. Finally, these assertions are illustrated by simulation experiments.
Frugal day-ahead forecasting of multiple local electricity loads by aggregating adaptive models
Feb 16, 2023Abstract:We focus on day-ahead electricity load forecasting of substations of the distribution network in France; therefore, our problem lies between the instability of a single consumption and the stability of a countrywide total demand. Moreover, we are interested in forecasting the loads of over one thousand substations; consequently, we are in the context of forecasting multiple time series. To that end, we rely on an adaptive methodology that provided excellent results at a national scale; the idea is to combine generalized additive models with state-space representations. However, the extension of this methodology to the prediction of over a thousand time series raises a computational issue. We solve it by developing a frugal variant, reducing the number of parameters estimated; we estimate the forecasting models only for a few time series and achieve transfer learning by relying on aggregation of experts. It yields a reduction of computational needs and their associated emissions. We build several variants, corresponding to different levels of parameter transfer, and we look for the best trade-off between accuracy and frugality. The selected method achieves competitive results compared to state-of-the-art individual models. Finally, we highlight the interpretability of the models, which is important for operational applications.
Adaptive Probabilistic Forecasting of Electricity (Net-)Load
Jan 24, 2023Abstract:We focus on electricity load forecasting under three important specificities. First, our setting is adaptive; we use models taking into account the most recent observations available, yielding a forecasting strategy able to automatically respond to regime changes. Second, we consider probabilistic rather than point forecasting; indeed, uncertainty quantification is required to operate electricity systems efficiently and reliably. Third, we consider both conventional load (consumption only) and netload (consumption less embedded generation). Our methodology relies on the Kalman filter, previously used successfully for adaptive point load forecasting. The probabilistic forecasts are obtained by quantile regressions on the residuals of the point forecasting model. We achieve adaptive quantile regressions using the online gradient descent; we avoid the choice of the gradient step size considering multiple learning rates and aggregation of experts. We apply the method to two data sets: the regional net-load in Great Britain and the demand of seven large cities in the United States. Adaptive procedures improve forecast performance substantially in both use cases and for both point and probabilistic forecasting.
State-Space Models Win the IEEE DataPort Competition on Post-covid Day-ahead Electricity Load Forecasting
Oct 01, 2021


Abstract:We present the winning strategy of an electricity demand forecasting competition. This competition was organized to design new forecasting methods for unstable periods such as the one starting in Spring 2020. We rely on state-space models to adapt standard statistical and machine learning models. We claim that it achieves the right compromise between two extremes. On the one hand, purely time-series models such as autoregressives are adaptive in essence but fail to capture dependence to exogenous variables. On the other hand, machine learning methods allow to learn complex dependence to explanatory variables on a historical data set but fail to forecast non-stationary data accurately. The evaluation period of the competition was the occasion of trial and error and we put the focus on the final forecasting procedure. In particular, it was at the same time that a recent algorithm was designed to adapt the variances of a state-space model and we present the results of the final version only. We discuss day-today predictions nonetheless.
Recursive Estimation of State-Space Noise Covariance Matrix by Approximate Variational Bayes
Apr 16, 2021
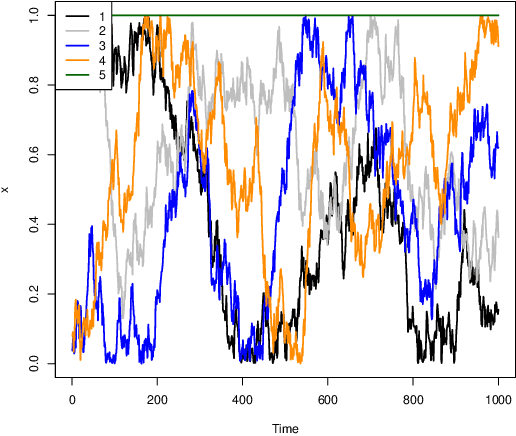

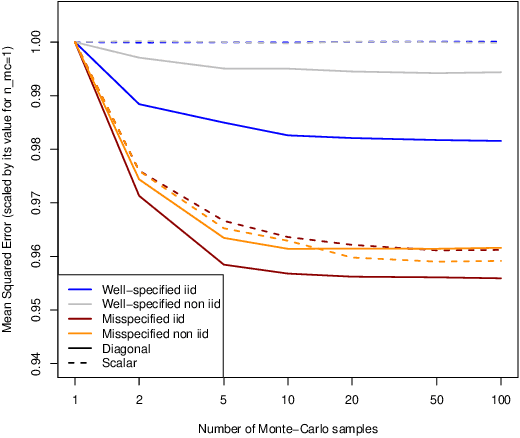
Abstract:This working paper considers state-space models where the variance of the observation is known but the covariance matrix of the state process is unknown and potentially time-varying. We propose an adaptive algorithm to estimate jointly the state and the covariance matrix of the state process, relying on Variational Bayes and second-order Taylor approximations.
Adaptive Methods for Short-Term Electricity Load Forecasting During COVID-19 Lockdown in France
Sep 14, 2020
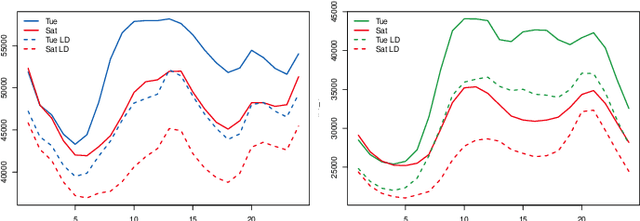
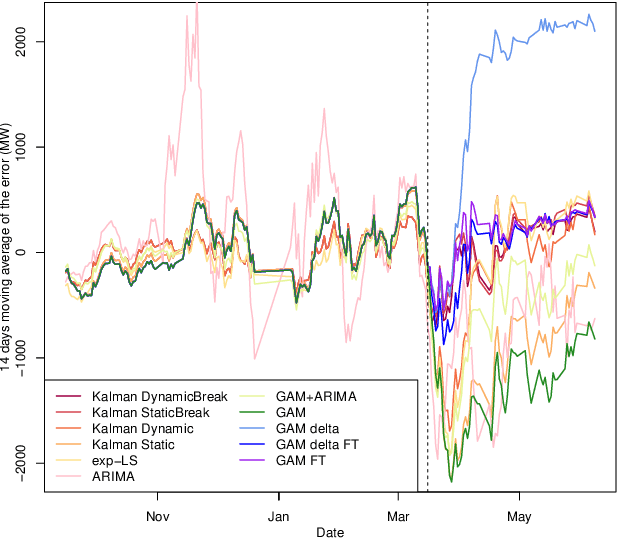
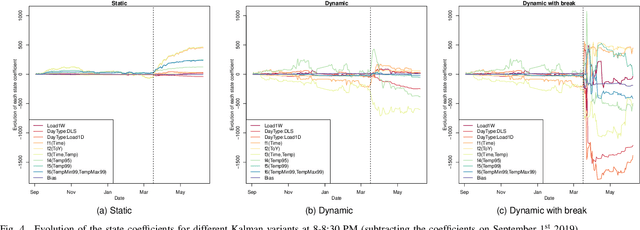
Abstract:The coronavirus disease 2019 (COVID-19) pandemic has urged many governments in the world to enforce a strict lockdown where all nonessential businesses are closed and citizens are ordered to stay at home. One of the consequences of this policy is a significant change in electricity consumption patterns. Since load forecasting models rely on calendar or meteorological information and are trained on historical data, they fail to capture the significant break caused by the lockdown and have exhibited poor performances since the beginning of the pandemic. This makes the scheduling of the electricity production challenging, and has a high cost for both electricity producers and grid operators. In this paper we introduce adaptive generalized additive models using Kalman filters and fine-tuning to adjust to new electricity consumption patterns. Additionally, knowledge from the lockdown in Italy is transferred to anticipate the change of behavior in France. The proposed methods are applied to forecast the electricity demand during the French lockdown period, where they demonstrate their ability to significantly reduce prediction errors compared to traditional models. Finally expert aggregation is used to leverage the specificities of each predictions and enhance results even further.
Stochastic Online Optimization using Kalman Recursion
Feb 10, 2020
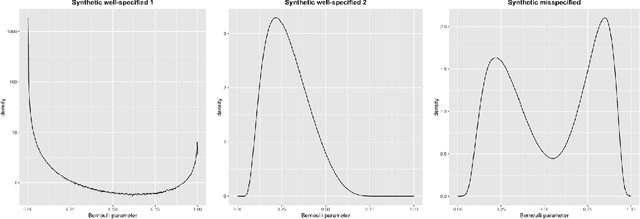
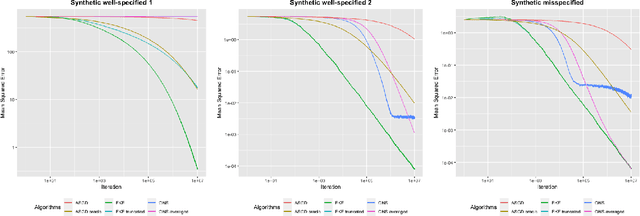

Abstract:We study the Extended Kalman Filter in constant dynamics, offering a bayesian perspective of stochastic optimization. We obtain high probability bounds on the cumulative excess risk in an unconstrained setting. The unconstrained challenge is tackled through a two-phase analysis. First, for linear and logistic regressions, we prove that the algorithm enters a local phase where the estimate stays in a small region around the optimum. We provide explicit bounds with high probability on this convergence time. Second, for generalized linear regressions, we provide a martingale analysis of the excess risk in the local phase, improving existing ones in bounded stochastic optimization. The EKF appears as a parameter-free O(d^2) online algorithm that optimally solves some unconstrained optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge