Optimized projection-free algorithms for online learning: construction and worst-case analysis

This work studies and develop projection-free algorithms for online learning with linear optimization oracles (a.k.a. Frank-Wolfe) for handling the constraint set. More precisely, this work (i) provides an improved (optimized) variant of an online Frank-Wolfe algorithm along with its conceptually simple potential-based proof, and (ii) shows how to leverage semidefinite programming to jointly design and analyze online Frank-Wolfe-type algorithms numerically in a variety of settings-that include the design of the variant (i). Based on the semidefinite technique, we conclude with strong numerical evidence suggesting that no pure online Frank-Wolfe algorithm within our model class can have a regret guarantee better than O(T^3/4) (T is the time horizon) without additional assumptions, that the current algorithms do not have optimal constants, that the algorithm benefits from similar anytime properties O(t^3/4) not requiring to know T in advance, and that multiple linear optimization rounds do not generally help to obtain better regret bounds.

Minimax Adaptive Online Nonparametric Regression over Besov Spaces

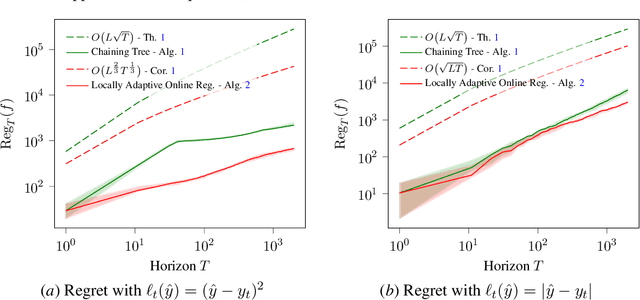
We study online adversarial regression with convex losses against a rich class of continuous yet highly irregular prediction rules, modeled by Besov spaces $B_{pq}^s$ with general parameters $1 \leq p,q \leq \infty$ and smoothness $s > d/p$. We introduce an adaptive wavelet-based algorithm that performs sequential prediction without prior knowledge of $(s,p,q)$, and establish minimax-optimal regret bounds against any comparator in $B_{pq}^s$. We further design a locally adaptive extension capable of dynamically tracking spatially inhomogeneous smoothness. This adaptive mechanism adjusts the resolution of the predictions over both time and space, yielding refined regret bounds in terms of local regularity. Consequently, in heterogeneous environments, our adaptive guarantees can significantly surpass those obtained by standard global methods.

Online Episodic Convex Reinforcement Learning

We study online learning in episodic finite-horizon Markov decision processes (MDPs) with convex objective functions, known as the concave utility reinforcement learning (CURL) problem. This setting generalizes RL from linear to convex losses on the state-action distribution induced by the agent's policy. The non-linearity of CURL invalidates classical Bellman equations and requires new algorithmic approaches. We introduce the first algorithm achieving near-optimal regret bounds for online CURL without any prior knowledge on the transition function. To achieve this, we use an online mirror descent algorithm with varying constraint sets and a carefully designed exploration bonus. We then address for the first time a bandit version of CURL, where the only feedback is the value of the objective function on the state-action distribution induced by the agent's policy. We achieve a sub-linear regret bound for this more challenging problem by adapting techniques from bandit convex optimization to the MDP setting.

Logarithmic Regret for Unconstrained Submodular Maximization Stochastic Bandit

We address the online unconstrained submodular maximization problem (Online USM), in a setting with stochastic bandit feedback. In this framework, a decision-maker receives noisy rewards from a nonmonotone submodular function, taking values in a known bounded interval. This paper proposes Double-Greedy - Explore-then-Commit (DG-ETC), adapting the Double-Greedy approach from the offline and online full-information settings. DG-ETC satisfies a O(d log(dT)) problemdependent upper bound for the 1/2-approximate pseudo-regret, as well as a O(dT^{2/3}log(dT)^{1/3}) problem-free one at the same time, outperforming existing approaches. To that end, we introduce a notion of hardness for submodular functions, characterizing how difficult it is to maximize them with this type of strategy.

Minimax Adaptive Boosting for Online Nonparametric Regression

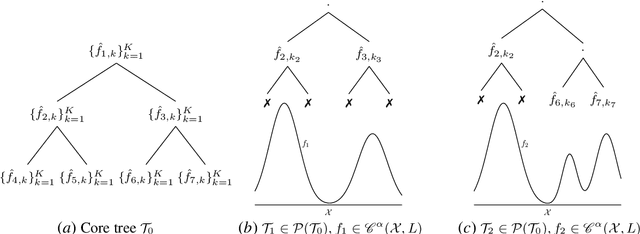
We study boosting for adversarial online nonparametric regression with general convex losses. We first introduce a parameter-free online gradient boosting (OGB) algorithm and show that its application to chaining trees achieves minimax optimal regret when competing against Lipschitz functions. While competing with nonparametric function classes can be challenging, the latter often exhibit local patterns, such as local Lipschitzness, that online algorithms can exploit to improve performance. By applying OGB over a core tree based on chaining trees, our proposed method effectively competes against all prunings that align with different Lipschitz profiles and demonstrates optimal dependence on the local regularities. As a result, we obtain the first computationally efficient algorithm with locally adaptive optimal rates for online regression in an adversarial setting.

Structured Prediction in Online Learning

We study a theoretical and algorithmic framework for structured prediction in the online learning setting. The problem of structured prediction, i.e. estimating function where the output space lacks a vectorial structure, is well studied in the literature of supervised statistical learning. We show that our algorithm is a generalisation of optimal algorithms from the supervised learning setting, and achieves the same excess risk upper bound also when data are not i.i.d. Moreover, we consider a second algorithm designed especially for non-stationary data distributions, including adversarial data. We bound its stochastic regret in function of the variation of the data distributions.

MetaCURL: Non-stationary Concave Utility Reinforcement Learning

We explore online learning in episodic loop-free Markov decision processes on non-stationary environments (changing losses and probability transitions). Our focus is on the Concave Utility Reinforcement Learning problem (CURL), an extension of classical RL for handling convex performance criteria in state-action distributions induced by agent policies. While various machine learning problems can be written as CURL, its non-linearity invalidates traditional Bellman equations. Despite recent solutions to classical CURL, none address non-stationary MDPs. This paper introduces MetaCURL, the first CURL algorithm for non-stationary MDPs. It employs a meta-algorithm running multiple black-box algorithms instances over different intervals, aggregating outputs via a sleeping expert framework. The key hurdle is partial information due to MDP uncertainty. Under partial information on the probability transitions (uncertainty and non-stationarity coming only from external noise, independent of agent state-action pairs), we achieve optimal dynamic regret without prior knowledge of MDP changes. Unlike approaches for RL, MetaCURL handles full adversarial losses, not just stochastic ones. We believe our approach for managing non-stationarity with experts can be of interest to the RL community.

Stop Relying on No-Choice and Do not Repeat the Moves: Optimal, Efficient and Practical Algorithms for Assortment Optimization

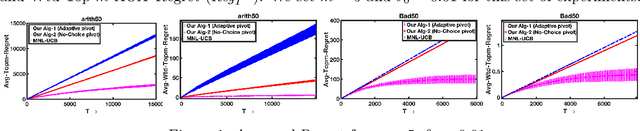
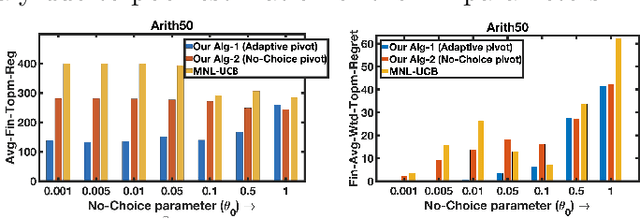
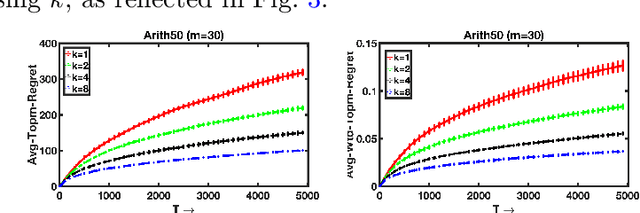
We address the problem of active online assortment optimization problem with preference feedback, which is a framework for modeling user choices and subsetwise utility maximization. The framework is useful in various real-world applications including ad placement, online retail, recommender systems, fine-tuning language models, amongst many. The problem, although has been studied in the past, lacks an intuitive and practical solution approach with simultaneously efficient algorithm and optimal regret guarantee. E.g., popularly used assortment selection algorithms often require the presence of a `strong reference' which is always included in the choice sets, further they are also designed to offer the same assortments repeatedly until the reference item gets selected -- all such requirements are quite unrealistic for practical applications. In this paper, we designed efficient algorithms for the problem of regret minimization in assortment selection with \emph{Plackett Luce} (PL) based user choices. We designed a novel concentration guarantee for estimating the score parameters of the PL model using `\emph{Pairwise Rank-Breaking}', which builds the foundation of our proposed algorithms. Moreover, our methods are practical, provably optimal, and devoid of the aforementioned limitations of the existing methods. Empirical evaluations corroborate our findings and outperform the existing baselines.

Covariance-Adaptive Least-Squares Algorithm for Stochastic Combinatorial Semi-Bandits

We address the problem of stochastic combinatorial semi-bandits, where a player can select from P subsets of a set containing d base items. Most existing algorithms (e.g. CUCB, ESCB, OLS-UCB) require prior knowledge on the reward distribution, like an upper bound on a sub-Gaussian proxy-variance, which is hard to estimate tightly. In this work, we design a variance-adaptive version of OLS-UCB, relying on an online estimation of the covariance structure. Estimating the coefficients of a covariance matrix is much more manageable in practical settings and results in improved regret upper bounds compared to proxy variance-based algorithms. When covariance coefficients are all non-negative, we show that our approach efficiently leverages the semi-bandit feedback and provably outperforms bandit feedback approaches, not only in exponential regimes where P $\gg$ d but also when P $\le$ d, which is not straightforward from most existing analyses.

Online Learning Approach for Survival Analysis

We introduce an online mathematical framework for survival analysis, allowing real time adaptation to dynamic environments and censored data. This framework enables the estimation of event time distributions through an optimal second order online convex optimization algorithm-Online Newton Step (ONS). This approach, previously unexplored, presents substantial advantages, including explicit algorithms with non-asymptotic convergence guarantees. Moreover, we analyze the selection of ONS hyperparameters, which depends on the exp-concavity property and has a significant influence on the regret bound. We propose a stochastic approach that guarantees logarithmic stochastic regret for ONS. Additionally, we introduce an adaptive aggregation method that ensures robustness in hyperparameter selection while maintaining fast regret bounds. The findings of this paper can extend beyond the survival analysis field, and are relevant for any case characterized by poor exp-concavity and unstable ONS. Finally, these assertions are illustrated by simulation experiments.