Towards Characterizing the First-order Query Complexity of Learning (Approximate) Nash Equilibria in Zero-sum Matrix Games

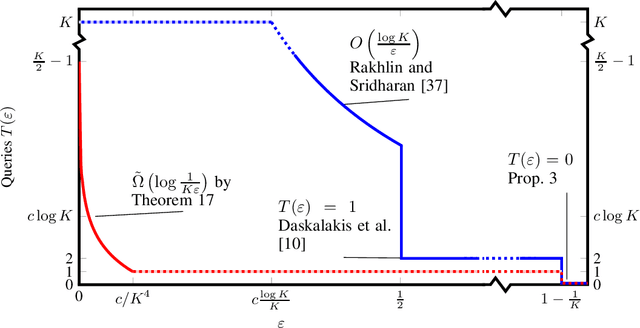
In the first-order query model for zero-sum $K\times K$ matrix games, playersobserve the expected pay-offs for all their possible actions under therandomized action played by their opponent. This is a classical model,which has received renewed interest after the discoveryby Rakhlin and Sridharan that $\epsilon$-approximate Nash equilibria can be computedefficiently from $O(\ln K / \epsilon) $ instead of $O( \ln K / \epsilon^2)$ queries.Surprisingly, the optimal number of such queries, as a function of both$\epsilon$ and $K$, is not known.We make progress on this question on two fronts. First, we fully characterise the query complexity of learning exact equilibria ($\epsilon=0$), by showing that they require a number of queries that is linearin $K$, which means that it is essentially as hard as querying the wholematrix, which can also be done with $K$ queries. Second, for $\epsilon > 0$, the currentquery complexity upper bound stands at $O(\min(\ln(K) / \epsilon , K))$. We argue that, unfortunately, obtaining matchinglower bound is not possible with existing techniques: we prove that nolower bound can be derived by constructing hard matrices whose entriestake values in a known countable set, because such matrices can be fullyidentified by a single query. This rules out, for instance, reducing toa submodular optimization problem over the hypercube by encoding itas a binary matrix. We then introduce a new technique for lower bounds,which allows us to obtain lower bounds of order$\tilde\Omega(\log(1 / (K\epsilon)))$ for any $\epsilon \leq1 / cK^4$, where $c$ is a constant independent of $K$. We furtherdiscuss possible future directions to improve on our techniques in orderto close the gap with the upper bounds.

Robust Online Convex Optimization in the Presence of Outliers

We consider online convex optimization when a number k of data points are outliers that may be corrupted. We model this by introducing the notion of robust regret, which measures the regret only on rounds that are not outliers. The aim for the learner is to achieve small robust regret, without knowing where the outliers are. If the outliers are chosen adversarially, we show that a simple filtering strategy on extreme gradients incurs O(k) additive overhead compared to the usual regret bounds, and that this is unimprovable, which means that k needs to be sublinear in the number of rounds. We further ask which additional assumptions would allow for a linear number of outliers. It turns out that the usual benign cases of independently, identically distributed (i.i.d.) observations or strongly convex losses are not sufficient. However, combining i.i.d. observations with the assumption that outliers are those observations that are in an extreme quantile of the distribution, does lead to sublinear robust regret, even though the expected number of outliers is linear.

MetaGrad: Adaptation using Multiple Learning Rates in Online Learning

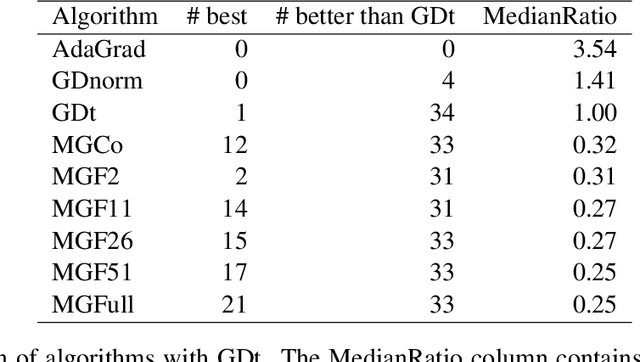
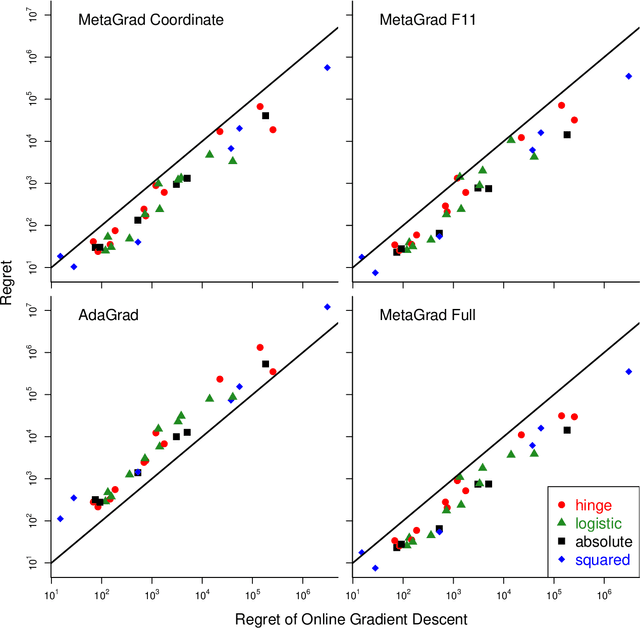
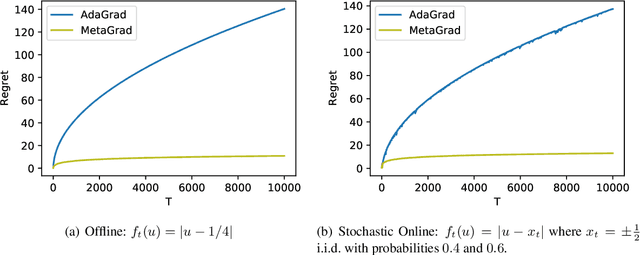
We provide a new adaptive method for online convex optimization, MetaGrad, that is robust to general convex losses but achieves faster rates for a broad class of special functions, including exp-concave and strongly convex functions, but also various types of stochastic and non-stochastic functions without any curvature. We prove this by drawing a connection to the Bernstein condition, which is known to imply fast rates in offline statistical learning. MetaGrad further adapts automatically to the size of the gradients. Its main feature is that it simultaneously considers multiple learning rates, which are weighted directly proportional to their empirical performance on the data using a new meta-algorithm. We provide three versions of MetaGrad. The full matrix version maintains a full covariance matrix and is applicable to learning tasks for which we can afford update time quadratic in the dimension. The other two versions provide speed-ups for high-dimensional learning tasks with an update time that is linear in the dimension: one is based on sketching, the other on running a separate copy of the basic algorithm per coordinate. We evaluate all versions of MetaGrad on benchmark online classification and regression tasks, on which they consistently outperform both online gradient descent and AdaGrad.

Regret Minimization in Heavy-Tailed Bandits

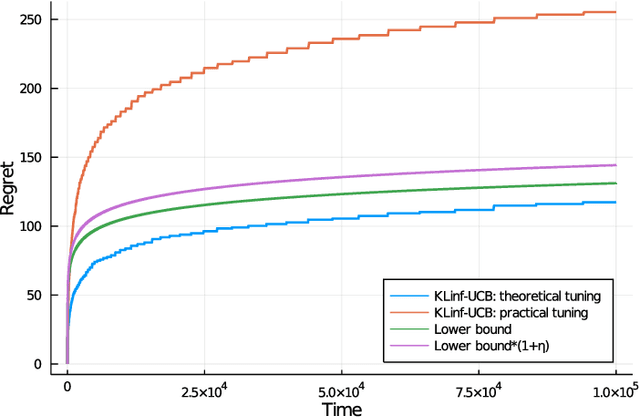
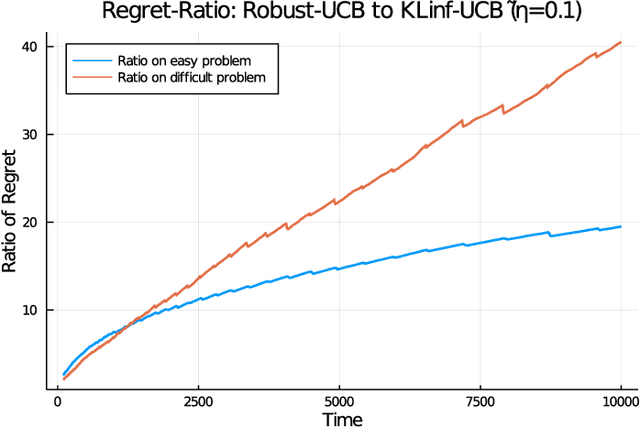
We revisit the classic regret-minimization problem in the stochastic multi-armed bandit setting when the arm-distributions are allowed to be heavy-tailed. Regret minimization has been well studied in simpler settings of either bounded support reward distributions or distributions that belong to a single parameter exponential family. We work under the much weaker assumption that the moments of order $(1+\epsilon)$ are uniformly bounded by a known constant B, for some given $\epsilon > 0$. We propose an optimal algorithm that matches the lower bound exactly in the first-order term. We also give a finite-time bound on its regret. We show that our index concentrates faster than the well known truncated or trimmed empirical mean estimators for the mean of heavy-tailed distributions. Computing our index can be computationally demanding. To address this, we develop a batch-based algorithm that is optimal up to a multiplicative constant depending on the batch size. We hence provide a controlled trade-off between statistical optimality and computational cost.

Optimal Best-Arm Identification Methods for Tail-Risk Measures

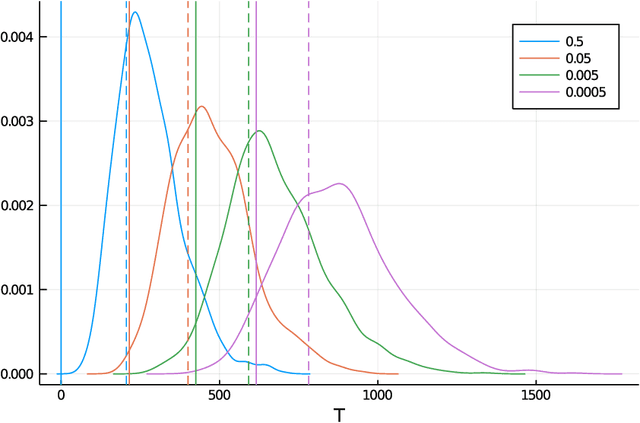
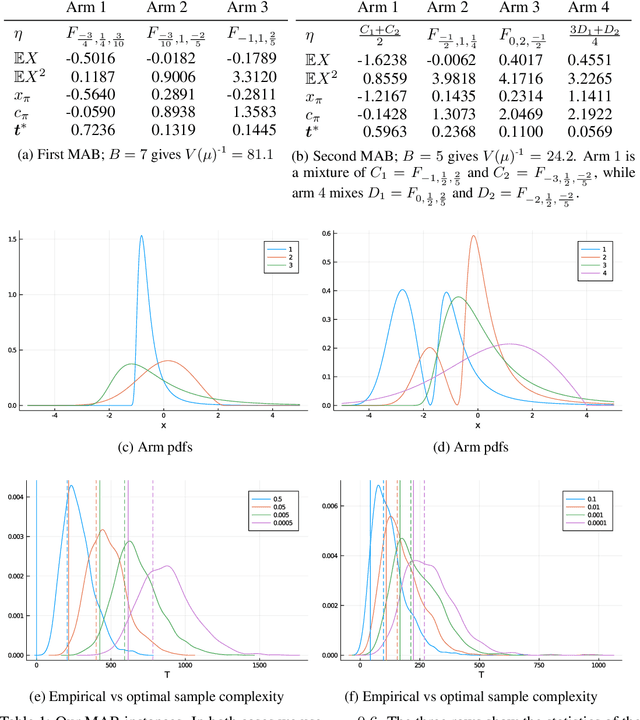
Conditional value-at-risk (CVaR) and value-at-risk (VaR) are popular tail-risk measures in finance and insurance industries where often the underlying probability distributions are heavy-tailed. We use the multi-armed bandit best-arm identification framework and consider the problem of identifying the arm-distribution from amongst finitely many that has the smallest CVaR or VaR. We first show that in the special case of arm-distributions belonging to a single-parameter exponential family, both these problems are equivalent to the best mean-arm identification problem, which is widely studied in the literature. This equivalence however is not true in general. We then propose optimal $\delta$-correct algorithms that act on general arm-distributions, including heavy-tailed distributions, that match the lower bound on the expected number of samples needed, asymptotically (as $ \delta$ approaches $0$). En-route, we also develop new non-asymptotic concentration inequalities for certain functions of these risk measures for the empirical distribution, that may have wider applicability.

Structure Adaptive Algorithms for Stochastic Bandits

We study reward maximisation in a wide class of structured stochastic multi-armed bandit problems, where the mean rewards of arms satisfy some given structural constraints, e.g. linear, unimodal, sparse, etc. Our aim is to develop methods that are flexible (in that they easily adapt to different structures), powerful (in that they perform well empirically and/or provably match instance-dependent lower bounds) and efficient in that the per-round computational burden is small. We develop asymptotically optimal algorithms from instance-dependent lower-bounds using iterative saddle-point solvers. Our approach generalises recent iterative methods for pure exploration to reward maximisation, where a major challenge arises from the estimation of the sub-optimality gaps and their reciprocals. Still we manage to achieve all the above desiderata. Notably, our technique avoids the computational cost of the full-blown saddle point oracle employed by previous work, while at the same time enabling finite-time regret bounds. Our experiments reveal that our method successfully leverages the structural assumptions, while its regret is at worst comparable to that of vanilla UCB.

Lipschitz and Comparator-Norm Adaptivity in Online Learning

We study Online Convex Optimization in the unbounded setting where neither predictions nor gradient are constrained. The goal is to simultaneously adapt to both the sequence of gradients and the comparator. We first develop parameter-free and scale-free algorithms for a simplified setting with hints. We present two versions: the first adapts to the squared norms of both comparator and gradients separately using $O(d)$ time per round, the second adapts to their squared inner products (which measure variance only in the comparator direction) in time $O(d^3)$ per round. We then generalize two prior reductions to the unbounded setting; one to not need hints, and a second to deal with the range ratio problem (which already arises in prior work). We discuss their optimality in light of prior and new lower bounds. We apply our methods to obtain sharper regret bounds for scale-invariant online prediction with linear models.

Non-Asymptotic Pure Exploration by Solving Games

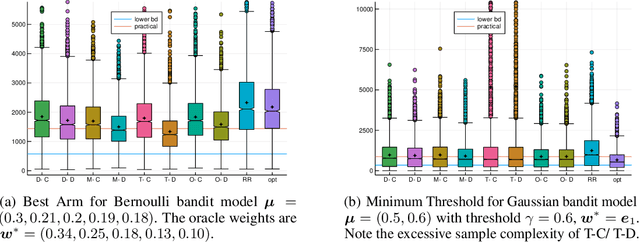
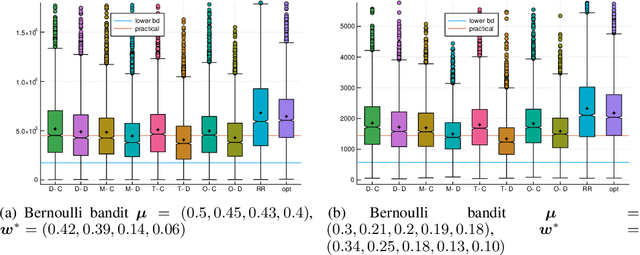
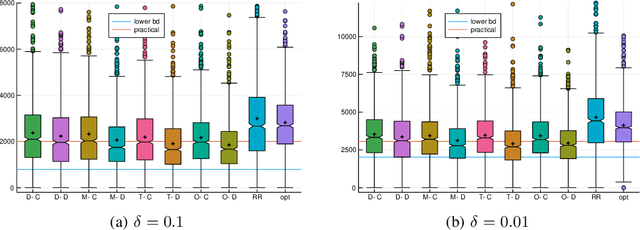
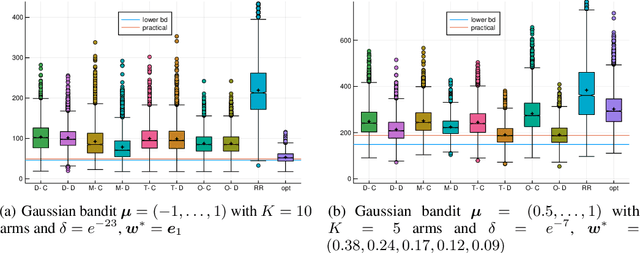
Pure exploration (aka active testing) is the fundamental task of sequentially gathering information to answer a query about a stochastic environment. Good algorithms make few mistakes and take few samples. Lower bounds (for multi-armed bandit models with arms in an exponential family) reveal that the sample complexity is determined by the solution to an optimisation problem. The existing state of the art algorithms achieve asymptotic optimality by solving a plug-in estimate of that optimisation problem at each step. We interpret the optimisation problem as an unknown game, and propose sampling rules based on iterative strategies to estimate and converge to its saddle point. We apply no-regret learners to obtain the first finite confidence guarantees that are adapted to the exponential family and which apply to any pure exploration query and bandit structure. Moreover, our algorithms only use a best response oracle instead of fully solving the optimisation problem.

Lipschitz Adaptivity with Multiple Learning Rates in Online Learning

We aim to design adaptive online learning algorithms that take advantage of any special structure that might be present in the learning task at hand, with as little manual tuning by the user as possible. A fundamental obstacle that comes up in the design of such adaptive algorithms is to calibrate a so-called step-size or learning rate hyperparameter depending on variance, gradient norms, etc. A recent technique promises to overcome this difficulty by maintaining multiple learning rates in parallel. This technique has been applied in the MetaGrad algorithm for online convex optimization and the Squint algorithm for prediction with expert advice. However, in both cases the user still has to provide in advance a Lipschitz hyperparameter that bounds the norm of the gradients. Although this hyperparameter is typically not available in advance, tuning it correctly is crucial: if it is set too small, the methods may fail completely; but if it is taken too large, performance deteriorates significantly. In the present work we remove this Lipschitz hyperparameter by designing new versions of MetaGrad and Squint that adapt to its optimal value automatically. We achieve this by dynamically updating the set of active learning rates. For MetaGrad, we further improve the computational efficiency of handling constraints on the domain of prediction, and we remove the need to specify the number of rounds in advance.

Pure Exploration with Multiple Correct Answers

We determine the sample complexity of pure exploration bandit problems with multiple good answers. We derive a lower bound using a new game equilibrium argument. We show how continuity and convexity properties of single-answer problems ensures that the Track-and-Stop algorithm has asymptotically optimal sample complexity. However, that convexity is lost when going to the multiple-answer setting. We present a new algorithm which extends Track-and-Stop to the multiple-answer case and has asymptotic sample complexity matching the lower bound.