Towards Characterizing the First-order Query Complexity of Learning (Approximate) Nash Equilibria in Zero-sum Matrix Games
Paper and Code
Apr 25, 2023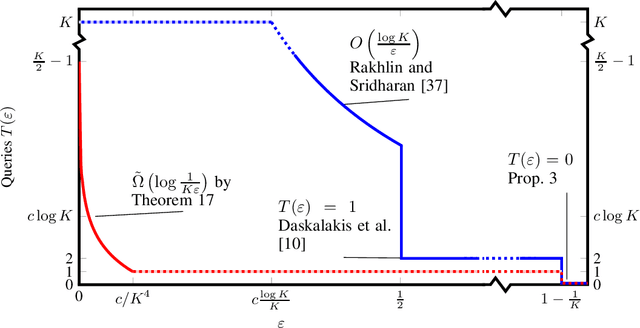
In the first-order query model for zero-sum $K\times K$ matrix games, playersobserve the expected pay-offs for all their possible actions under therandomized action played by their opponent. This is a classical model,which has received renewed interest after the discoveryby Rakhlin and Sridharan that $\epsilon$-approximate Nash equilibria can be computedefficiently from $O(\ln K / \epsilon) $ instead of $O( \ln K / \epsilon^2)$ queries.Surprisingly, the optimal number of such queries, as a function of both$\epsilon$ and $K$, is not known.We make progress on this question on two fronts. First, we fully characterise the query complexity of learning exact equilibria ($\epsilon=0$), by showing that they require a number of queries that is linearin $K$, which means that it is essentially as hard as querying the wholematrix, which can also be done with $K$ queries. Second, for $\epsilon > 0$, the currentquery complexity upper bound stands at $O(\min(\ln(K) / \epsilon , K))$. We argue that, unfortunately, obtaining matchinglower bound is not possible with existing techniques: we prove that nolower bound can be derived by constructing hard matrices whose entriestake values in a known countable set, because such matrices can be fullyidentified by a single query. This rules out, for instance, reducing toa submodular optimization problem over the hypercube by encoding itas a binary matrix. We then introduce a new technique for lower bounds,which allows us to obtain lower bounds of order$\tilde\Omega(\log(1 / (K\epsilon)))$ for any $\epsilon \leq1 / cK^4$, where $c$ is a constant independent of $K$. We furtherdiscuss possible future directions to improve on our techniques in orderto close the gap with the upper bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge