MetaCURL: Non-stationary Concave Utility Reinforcement Learning

We explore online learning in episodic loop-free Markov decision processes on non-stationary environments (changing losses and probability transitions). Our focus is on the Concave Utility Reinforcement Learning problem (CURL), an extension of classical RL for handling convex performance criteria in state-action distributions induced by agent policies. While various machine learning problems can be written as CURL, its non-linearity invalidates traditional Bellman equations. Despite recent solutions to classical CURL, none address non-stationary MDPs. This paper introduces MetaCURL, the first CURL algorithm for non-stationary MDPs. It employs a meta-algorithm running multiple black-box algorithms instances over different intervals, aggregating outputs via a sleeping expert framework. The key hurdle is partial information due to MDP uncertainty. Under partial information on the probability transitions (uncertainty and non-stationarity coming only from external noise, independent of agent state-action pairs), we achieve optimal dynamic regret without prior knowledge of MDP changes. Unlike approaches for RL, MetaCURL handles full adversarial losses, not just stochastic ones. We believe our approach for managing non-stationarity with experts can be of interest to the RL community.

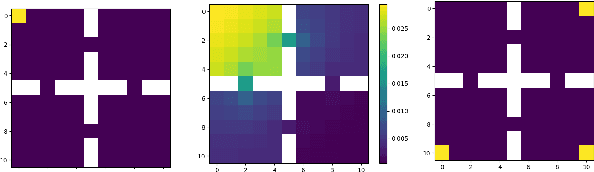
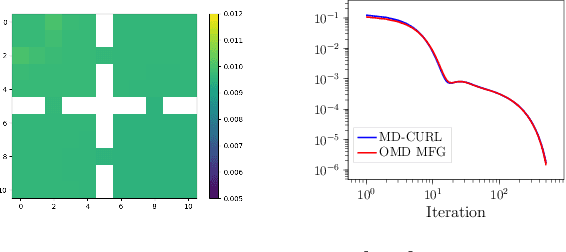
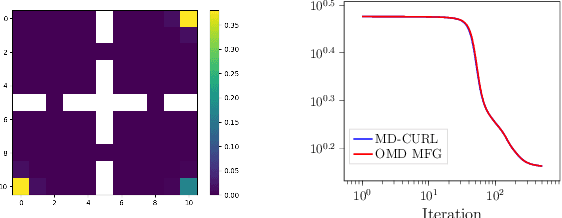
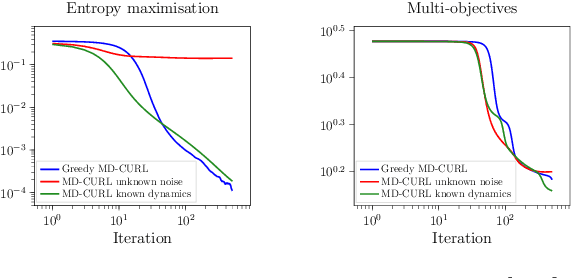
Efficient Model-Based Concave Utility Reinforcement Learning through Greedy Mirror Descent

Many machine learning tasks can be solved by minimizing a convex function of an occupancy measure over the policies that generate them. These include reinforcement learning, imitation learning, among others. This more general paradigm is called the Concave Utility Reinforcement Learning problem (CURL). Since CURL invalidates classical Bellman equations, it requires new algorithms. We introduce MD-CURL, a new algorithm for CURL in a finite horizon Markov decision process. MD-CURL is inspired by mirror descent and uses a non-standard regularization to achieve convergence guarantees and a simple closed-form solution, eliminating the need for computationally expensive projection steps typically found in mirror descent approaches. We then extend CURL to an online learning scenario and present Greedy MD-CURL, a new method adapting MD-CURL to an online, episode-based setting with partially unknown dynamics. Like MD-CURL, the online version Greedy MD-CURL benefits from low computational complexity, while guaranteeing sub-linear or even logarithmic regret, depending on the level of information available on the underlying dynamics.

A mirror descent approach for Mean Field Control applied to Demande-Side management

We consider a finite-horizon Mean Field Control problem for Markovian models. The objective function is composed of a sum of convex and Lipschitz functions taking their values on a space of state-action distributions. We introduce an iterative algorithm which we prove to be a Mirror Descent associated with a non-standard Bregman divergence, having a convergence rate of order 1/ $\sqrt$ K. It requires the solution of a simple dynamic programming problem at each iteration. We compare this algorithm with learning methods for Mean Field Games after providing a reformulation of our control problem as a game problem. These theoretical contributions are illustrated with numerical examples applied to a demand-side management problem for power systems aimed at controlling the average power consumption profile of a population of flexible devices contributing to the power system balance.