Minimax Adaptive Boosting for Online Nonparametric Regression
Paper and Code
Oct 04, 2024
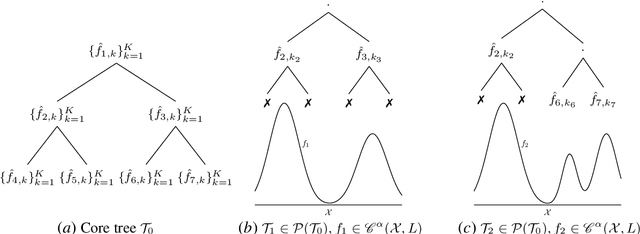
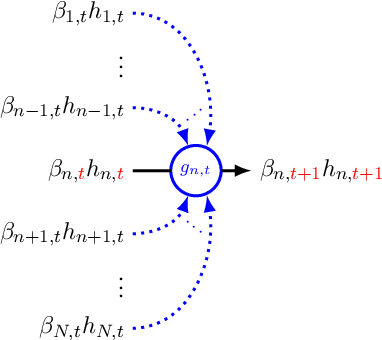
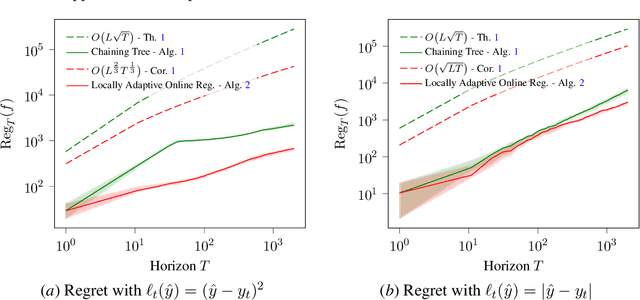
We study boosting for adversarial online nonparametric regression with general convex losses. We first introduce a parameter-free online gradient boosting (OGB) algorithm and show that its application to chaining trees achieves minimax optimal regret when competing against Lipschitz functions. While competing with nonparametric function classes can be challenging, the latter often exhibit local patterns, such as local Lipschitzness, that online algorithms can exploit to improve performance. By applying OGB over a core tree based on chaining trees, our proposed method effectively competes against all prunings that align with different Lipschitz profiles and demonstrates optimal dependence on the local regularities. As a result, we obtain the first computationally efficient algorithm with locally adaptive optimal rates for online regression in an adversarial setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge