SoftCVI: contrastive variational inference with self-generated soft labels

Estimating a distribution given access to its unnormalized density is pivotal in Bayesian inference, where the posterior is generally known only up to an unknown normalizing constant. Variational inference and Markov chain Monte Carlo methods are the predominant tools for this task; however, both methods are often challenging to apply reliably, particularly when the posterior has complex geometry. Here, we introduce Soft Contrastive Variational Inference (SoftCVI), which allows a family of variational objectives to be derived through a contrastive estimation framework. These objectives have zero variance gradient when the variational approximation is exact, without the need for specialized gradient estimators. The approach involves parameterizing a classifier in terms of the variational distribution, which allows the inference task to be reframed as a contrastive estimation problem, aiming to identify a single true posterior sample among a set of samples. Despite this framing, we do not require positive or negative samples, but rather learn by sampling the variational distribution and computing ground truth soft classification labels from the unnormalized posterior itself. We empirically investigate the performance on a variety of Bayesian inference tasks, using both using both simple (e.g. normal) and expressive (normalizing flow) variational distributions. We find that SoftCVI objectives often outperform other commonly used variational objectives.

Adaptive Probabilistic Forecasting of Electricity (Net-)Load

We focus on electricity load forecasting under three important specificities. First, our setting is adaptive; we use models taking into account the most recent observations available, yielding a forecasting strategy able to automatically respond to regime changes. Second, we consider probabilistic rather than point forecasting; indeed, uncertainty quantification is required to operate electricity systems efficiently and reliably. Third, we consider both conventional load (consumption only) and netload (consumption less embedded generation). Our methodology relies on the Kalman filter, previously used successfully for adaptive point load forecasting. The probabilistic forecasts are obtained by quantile regressions on the residuals of the point forecasting model. We achieve adaptive quantile regressions using the online gradient descent; we avoid the choice of the gradient step size considering multiple learning rates and aggregation of experts. We apply the method to two data sets: the regional net-load in Great Britain and the demand of seven large cities in the United States. Adaptive procedures improve forecast performance substantially in both use cases and for both point and probabilistic forecasting.

Robust Neural Posterior Estimation and Statistical Model Criticism

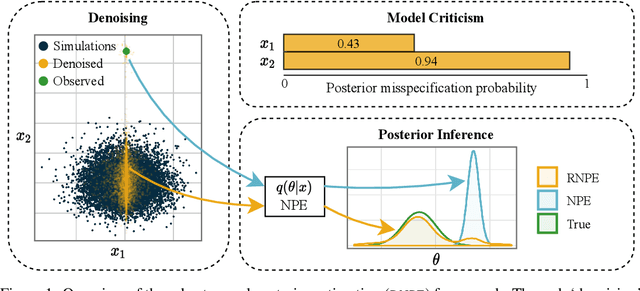
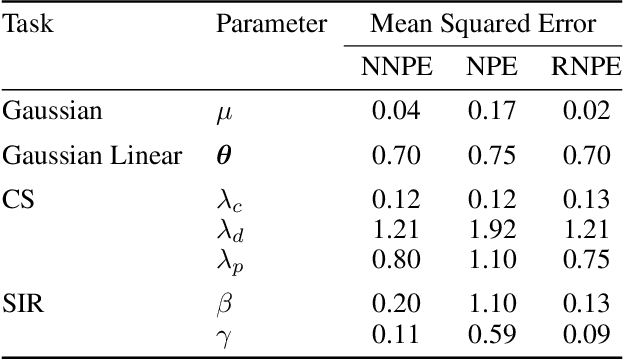
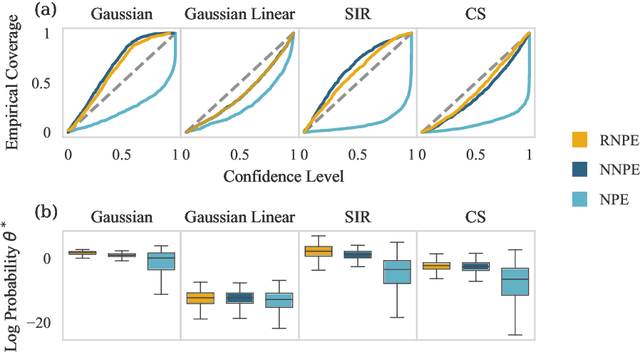
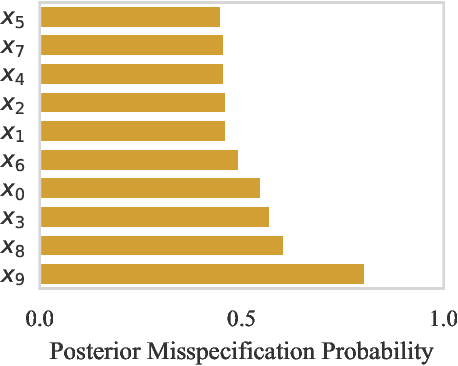
Computer simulations have proven a valuable tool for understanding complex phenomena across the sciences. However, the utility of simulators for modelling and forecasting purposes is often restricted by low data quality, as well as practical limits to model fidelity. In order to circumvent these difficulties, we argue that modellers must treat simulators as idealistic representations of the true data generating process, and consequently should thoughtfully consider the risk of model misspecification. In this work we revisit neural posterior estimation (NPE), a class of algorithms that enable black-box parameter inference in simulation models, and consider the implication of a simulation-to-reality gap. While recent works have demonstrated reliable performance of these methods, the analyses have been performed using synthetic data generated by the simulator model itself, and have therefore only addressed the well-specified case. In this paper, we find that the presence of misspecification, in contrast, leads to unreliable inference when NPE is used naively. As a remedy we argue that principled scientific inquiry with simulators should incorporate a model criticism component, to facilitate interpretable identification of misspecification and a robust inference component, to fit 'wrong but useful' models. We propose robust neural posterior estimation (RNPE), an extension of NPE to simultaneously achieve both these aims, through explicitly modelling the discrepancies between simulations and the observed data. We assess the approach on a range of artificially misspecified examples, and find RNPE performs well across the tasks, whereas naively using NPE leads to misleading and erratic posteriors.

Daily peak electrical load forecasting with a multi-resolution approach

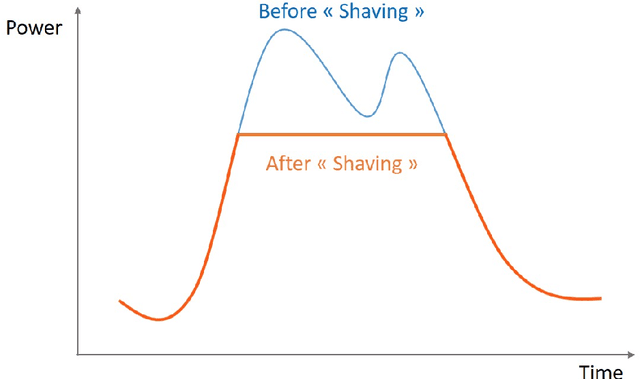
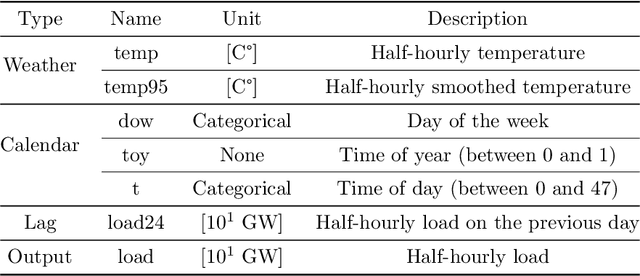
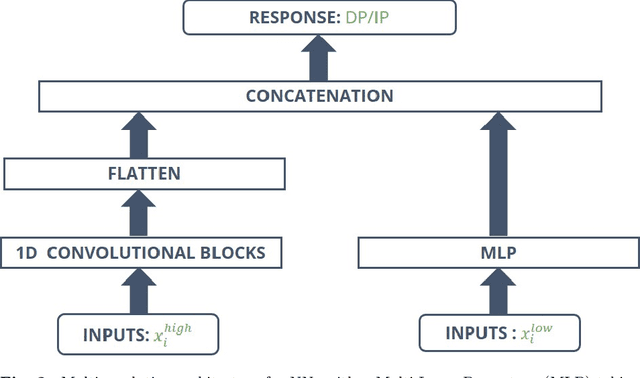
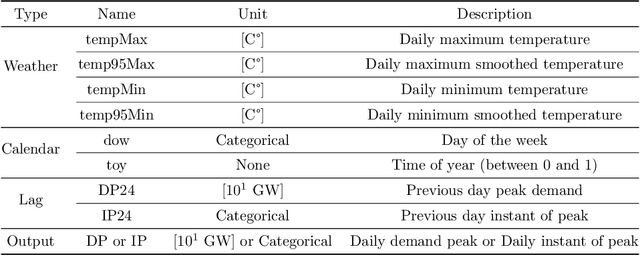
In the context of smart grids and load balancing, daily peak load forecasting has become a critical activity for stakeholders of the energy industry. An understanding of peak magnitude and timing is paramount for the implementation of smart grid strategies such as peak shaving. The modelling approach proposed in this paper leverages high-resolution and low-resolution information to forecast daily peak demand size and timing. The resulting multi-resolution modelling framework can be adapted to different model classes. The key contributions of this paper are a) a general and formal introduction to the multi-resolution modelling approach, b) a discussion on modelling approaches at different resolutions implemented via Generalised Additive Models and Neural Networks and c) experimental results on real data from the UK electricity market. The results confirm that the predictive performance of the proposed modelling approach is competitive with that of low- and high-resolution alternatives.

Additive stacking for disaggregate electricity demand forecasting

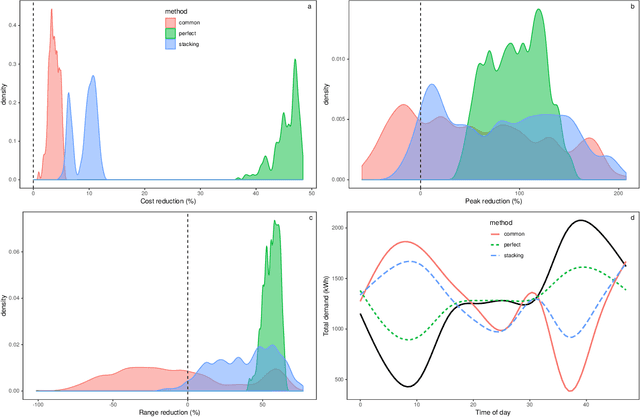
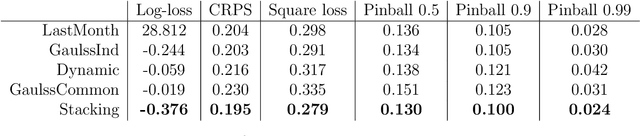
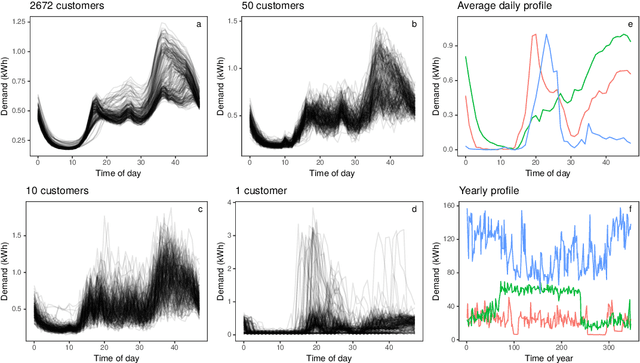
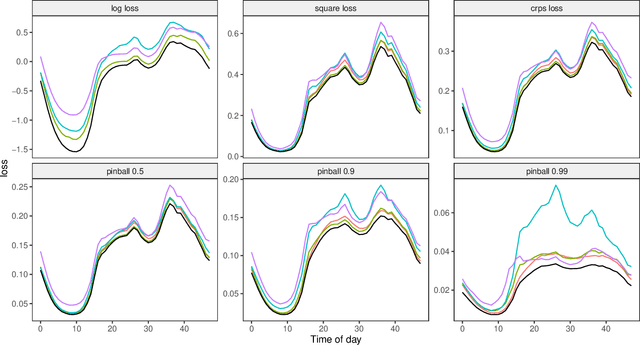
Future grid management systems will coordinate distributed production and storage resources to manage, in a cost effective fashion, the increased load and variability brought by the electrification of transportation and by a higher share of weather dependent production. Electricity demand forecasts at a low level of aggregation will be key inputs for such systems. We focus on forecasting demand at the individual household level, which is more challenging than forecasting aggregate demand, due to the lower signal-to-noise ratio and to the heterogeneity of consumption patterns across households. We propose a new ensemble method for probabilistic forecasting, which borrows strength across the households while accommodating their individual idiosyncrasies. In particular, we develop a set of models or 'experts' which capture different demand dynamics and we fit each of them to the data from each household. Then we construct an aggregation of experts where the ensemble weights are estimated on the whole data set, the main innovation being that we let the weights vary with the covariates by adopting an additive model structure. In particular, the proposed aggregation method is an extension of regression stacking (Breiman, 1996) where the mixture weights are modelled using linear combinations of parametric, smooth or random effects. The methods for building and fitting additive stacking models are implemented by the gamFactory R package, available at https://github.com/mfasiolo/gamFactory.