Direct Fisher Score Estimation for Likelihood Maximization

We study the problem of likelihood maximization when the likelihood function is intractable but model simulations are readily available. We propose a sequential, gradient-based optimization method that directly models the Fisher score based on a local score matching technique which uses simulations from a localized region around each parameter iterate. By employing a linear parameterization to the surrogate score model, our technique admits a closed-form, least-squares solution. This approach yields a fast, flexible, and efficient approximation to the Fisher score, effectively smoothing the likelihood objective and mitigating the challenges posed by complex likelihood landscapes. We provide theoretical guarantees for our score estimator, including bounds on the bias introduced by the smoothing. Empirical results on a range of synthetic and real-world problems demonstrate the superior performance of our method compared to existing benchmarks.

SoftCVI: contrastive variational inference with self-generated soft labels

Estimating a distribution given access to its unnormalized density is pivotal in Bayesian inference, where the posterior is generally known only up to an unknown normalizing constant. Variational inference and Markov chain Monte Carlo methods are the predominant tools for this task; however, both methods are often challenging to apply reliably, particularly when the posterior has complex geometry. Here, we introduce Soft Contrastive Variational Inference (SoftCVI), which allows a family of variational objectives to be derived through a contrastive estimation framework. These objectives have zero variance gradient when the variational approximation is exact, without the need for specialized gradient estimators. The approach involves parameterizing a classifier in terms of the variational distribution, which allows the inference task to be reframed as a contrastive estimation problem, aiming to identify a single true posterior sample among a set of samples. Despite this framing, we do not require positive or negative samples, but rather learn by sampling the variational distribution and computing ground truth soft classification labels from the unnormalized posterior itself. We empirically investigate the performance on a variety of Bayesian inference tasks, using both using both simple (e.g. normal) and expressive (normalizing flow) variational distributions. We find that SoftCVI objectives often outperform other commonly used variational objectives.

Variational Gradient Descent using Local Linear Models

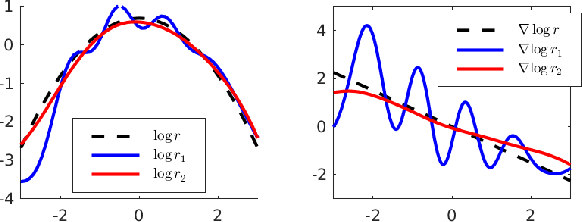
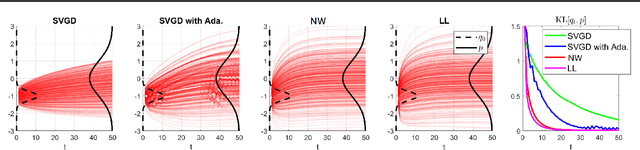
Stein Variational Gradient Descent (SVGD) can transport particles along trajectories that reduce the KL divergence between the target and particle distribution but requires the target score function to compute the update. We introduce a new perspective on SVGD that views it as a local estimator of the reversed KL gradient flow. This perspective inspires us to propose new estimators that use local linear models to achieve the same purpose. The proposed estimators can be computed using only samples from the target and particle distribution without needing the target score function. Our proposed variational gradient estimators utilize local linear models, resulting in computational simplicity while maintaining effectiveness comparable to SVGD in terms of estimation biases. Additionally, we demonstrate that under a mild assumption, the estimation of high-dimensional gradient flow can be translated into a lower-dimensional estimation problem, leading to improved estimation accuracy. We validate our claims with experiments on both simulated and real-world datasets.

Robust Neural Posterior Estimation and Statistical Model Criticism

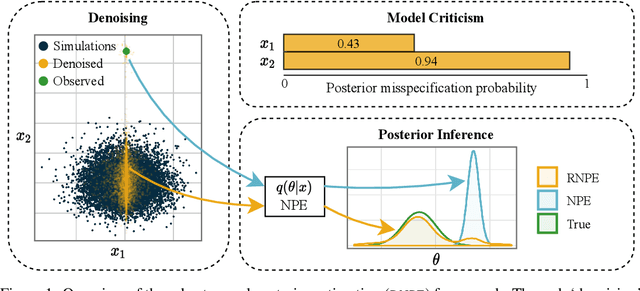
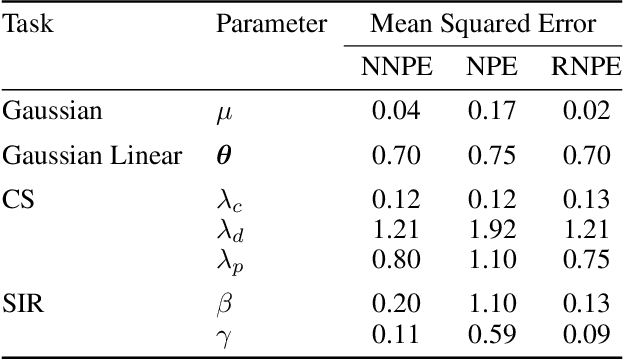
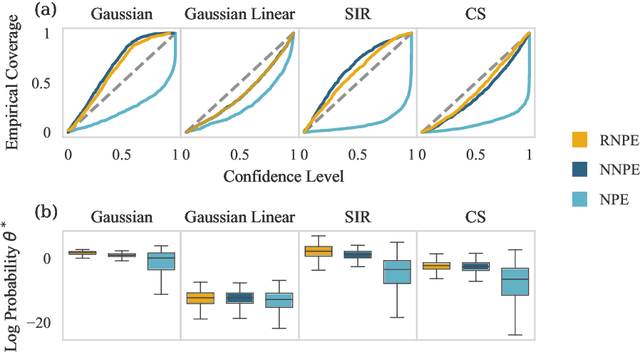
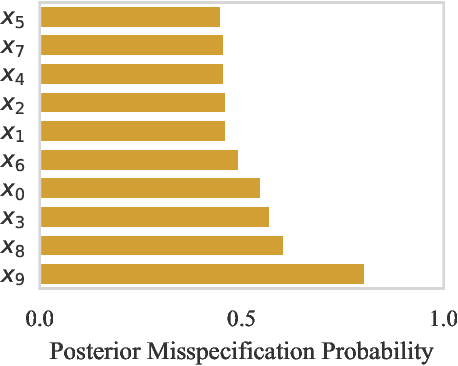
Computer simulations have proven a valuable tool for understanding complex phenomena across the sciences. However, the utility of simulators for modelling and forecasting purposes is often restricted by low data quality, as well as practical limits to model fidelity. In order to circumvent these difficulties, we argue that modellers must treat simulators as idealistic representations of the true data generating process, and consequently should thoughtfully consider the risk of model misspecification. In this work we revisit neural posterior estimation (NPE), a class of algorithms that enable black-box parameter inference in simulation models, and consider the implication of a simulation-to-reality gap. While recent works have demonstrated reliable performance of these methods, the analyses have been performed using synthetic data generated by the simulator model itself, and have therefore only addressed the well-specified case. In this paper, we find that the presence of misspecification, in contrast, leads to unreliable inference when NPE is used naively. As a remedy we argue that principled scientific inquiry with simulators should incorporate a model criticism component, to facilitate interpretable identification of misspecification and a robust inference component, to fit 'wrong but useful' models. We propose robust neural posterior estimation (RNPE), an extension of NPE to simultaneously achieve both these aims, through explicitly modelling the discrepancies between simulations and the observed data. We assess the approach on a range of artificially misspecified examples, and find RNPE performs well across the tasks, whereas naively using NPE leads to misleading and erratic posteriors.

Sequential Neural Score Estimation: Likelihood-Free Inference with Conditional Score Based Diffusion Models

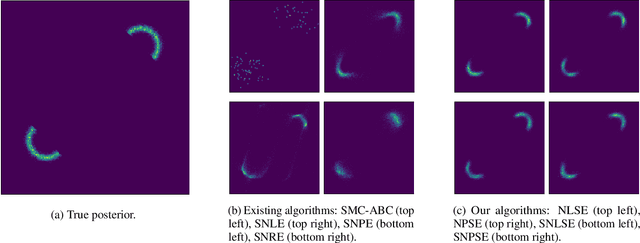
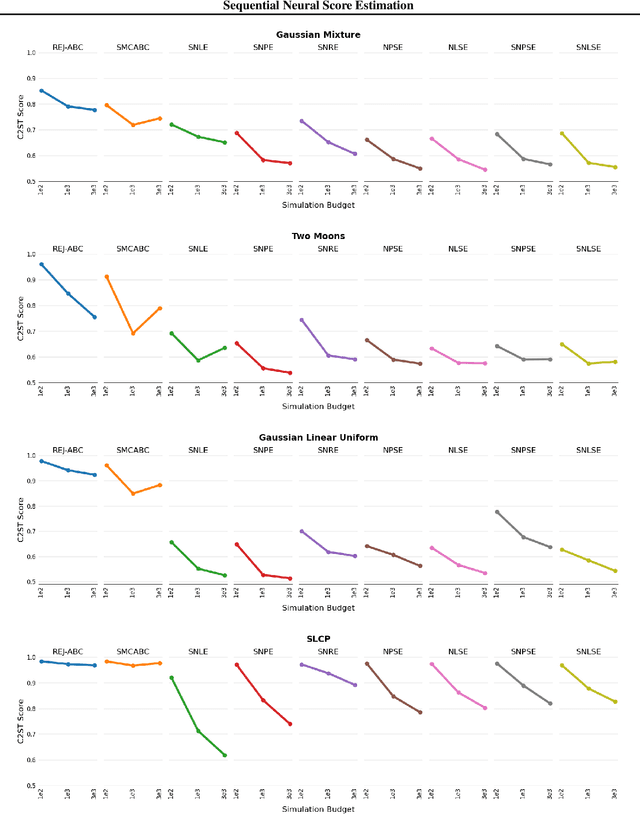
We introduce Sequential Neural Posterior Score Estimation (SNPSE) and Sequential Neural Likelihood Score Estimation (SNLSE), two new score-based methods for Bayesian inference in simulator-based models. Our methods, inspired by the success of score-based methods in generative modelling, leverage conditional score-based diffusion models to generate samples from the posterior distribution of interest. These models can be trained using one of two possible objective functions, one of which approximates the score of the intractable likelihood, while the other directly estimates the score of the posterior. We embed these models into a sequential training procedure, which guides simulations using the current approximation of the posterior at the observation of interest, thereby reducing the simulation cost. We validate our methods, as well as their amortised, non-sequential variants, on several numerical examples, demonstrating comparable or superior performance to existing state-of-the-art methods such as Sequential Neural Posterior Estimation (SNPE) and Sequential Neural Likelihood Estimation (SNLE).