PerturBench: Benchmarking Machine Learning Models for Cellular Perturbation Analysis

We present a comprehensive framework for predicting the effects of perturbations in single cells, designed to standardize benchmarking in this rapidly evolving field. Our framework, PerturBench, includes a user-friendly platform, diverse datasets, metrics for fair model comparison, and detailed performance analysis. Extensive evaluations of published and baseline models reveal limitations like mode or posterior collapse, and underscore the importance of rank metrics that assess the ordering of perturbations alongside traditional measures like RMSE. Our findings show that simple models can outperform more complex approaches. This benchmarking exercise sets new standards for model evaluation, supports robust model development, and advances the potential of these models to use high-throughput and high-content genetic and chemical screens for disease target discovery.

Robust Neural Posterior Estimation and Statistical Model Criticism

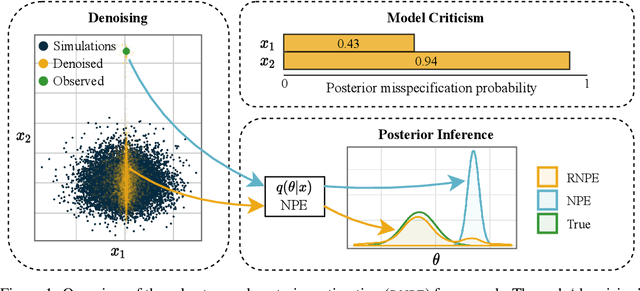
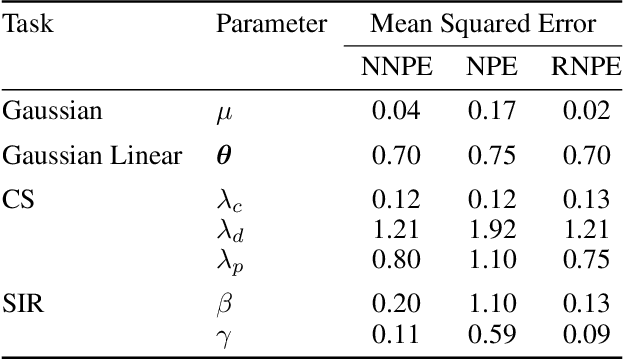
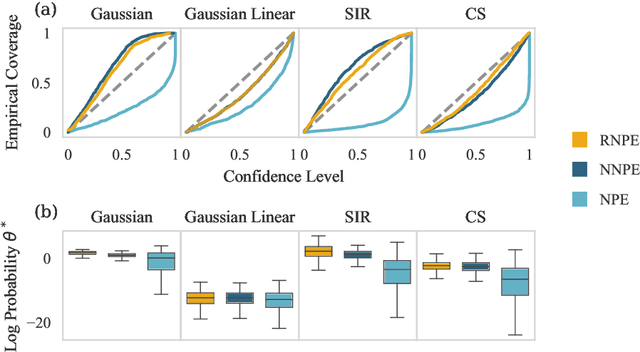
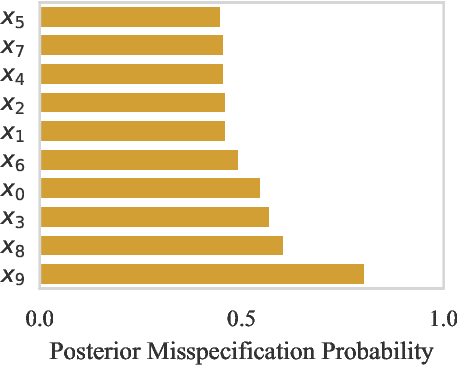
Computer simulations have proven a valuable tool for understanding complex phenomena across the sciences. However, the utility of simulators for modelling and forecasting purposes is often restricted by low data quality, as well as practical limits to model fidelity. In order to circumvent these difficulties, we argue that modellers must treat simulators as idealistic representations of the true data generating process, and consequently should thoughtfully consider the risk of model misspecification. In this work we revisit neural posterior estimation (NPE), a class of algorithms that enable black-box parameter inference in simulation models, and consider the implication of a simulation-to-reality gap. While recent works have demonstrated reliable performance of these methods, the analyses have been performed using synthetic data generated by the simulator model itself, and have therefore only addressed the well-specified case. In this paper, we find that the presence of misspecification, in contrast, leads to unreliable inference when NPE is used naively. As a remedy we argue that principled scientific inquiry with simulators should incorporate a model criticism component, to facilitate interpretable identification of misspecification and a robust inference component, to fit 'wrong but useful' models. We propose robust neural posterior estimation (RNPE), an extension of NPE to simultaneously achieve both these aims, through explicitly modelling the discrepancies between simulations and the observed data. We assess the approach on a range of artificially misspecified examples, and find RNPE performs well across the tasks, whereas naively using NPE leads to misleading and erratic posteriors.

Amortised Likelihood-free Inference for Expensive Time-series Simulators with Signatured Ratio Estimation

Simulation models of complex dynamics in the natural and social sciences commonly lack a tractable likelihood function, rendering traditional likelihood-based statistical inference impossible. Recent advances in machine learning have introduced novel algorithms for estimating otherwise intractable likelihood functions using a likelihood ratio trick based on binary classifiers. Consequently, efficient likelihood approximations can be obtained whenever good probabilistic classifiers can be constructed. We propose a kernel classifier for sequential data using path signatures based on the recently introduced signature kernel. We demonstrate that the representative power of signatures yields a highly performant classifier, even in the crucially important case where sample numbers are low. In such scenarios, our approach can outperform sophisticated neural networks for common posterior inference tasks.

Approximate Bayesian Computation with Path Signatures

Simulation models of scientific interest often lack a tractable likelihood function, precluding standard likelihood-based statistical inference. A popular likelihood-free method for inferring simulator parameters is approximate Bayesian computation, where an approximate posterior is sampled by comparing simulator output and observed data. However, effective measures of closeness between simulated and observed data are generally difficult to construct, particularly for time series data which are often high-dimensional and structurally complex. Existing approaches typically involve manually constructing summary statistics, requiring substantial domain expertise and experimentation, or rely on unrealistic assumptions such as iid data. Others are inappropriate in more complex settings like multivariate or irregularly sampled time series data. In this paper, we introduce the use of path signatures as a natural candidate feature set for constructing distances between time series data for use in approximate Bayesian computation algorithms. Our experiments show that such an approach can generate more accurate approximate Bayesian posteriors than existing techniques for time series models.

Optimal scaling of random walk Metropolis algorithms using Bayesian large-sample asymptotics

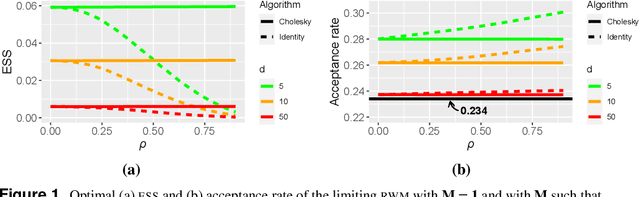
High-dimensional limit theorems have been shown to be useful to derive tuning rules for finding the optimal scaling in random walk Metropolis algorithms. The assumptions under which weak convergence results are proved are however restrictive; the target density is typically assumed to be of a product form. Users may thus doubt the validity of such tuning rules in practical applications. In this paper, we shed some light on optimal scaling problems from a different perspective, namely a large-sample one. This allows to prove weak convergence results under realistic assumptions and to propose novel parameter-dimension-dependent tuning guidelines. The proposed guidelines are consistent with previous ones when the target density is close to having a product form, but significantly different otherwise.

Generalized Posteriors in Approximate Bayesian Computation

Complex simulators have become a ubiquitous tool in many scientific disciplines, providing high-fidelity, implicit probabilistic models of natural and social phenomena. Unfortunately, they typically lack the tractability required for conventional statistical analysis. Approximate Bayesian computation (ABC) has emerged as a key method in simulation-based inference, wherein the true model likelihood and posterior are approximated using samples from the simulator. In this paper, we draw connections between ABC and generalized Bayesian inference (GBI). First, we re-interpret the accept/reject step in ABC as an implicitly defined error model. We then argue that these implicit error models will invariably be misspecified. While ABC posteriors are often treated as a necessary evil for approximating the standard Bayesian posterior, this allows us to re-interpret ABC as a potential robustification strategy. This leads us to suggest the use of GBI within ABC, a use case we explore empirically.

Neural ODEs for Multi-State Survival Analysis

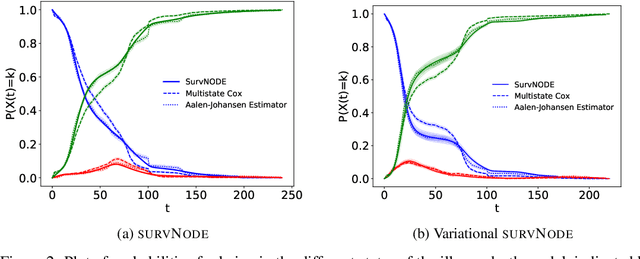
Survival models are a popular tool for the analysis of time to event data with applications in medicine, engineering, economics and many more. Advances like the Cox proportional hazard model have enabled researchers to better describe hazard rates for the occurrence of single fatal events, but are limited by modeling assumptions, like proportionality of hazard rates and linear effects. Moreover, common phenomena are often better described through multiple states, for example, the progress of a disease might be modeled as healthy, sick and dead instead of healthy and dead, where the competing nature of death and disease has to be taken into account. Also, individual characteristics can vary significantly between observational units, like patients, resulting in idiosyncratic hazard rates and different disease trajectories. These considerations require flexible modeling assumptions. Current standard models, however, are often ill-suited for such an analysis. To overcome these issues, we propose the use of neural ordinary differential equations as a flexible and general method for estimating multi-state survival models by directly solving the Kolmogorov forward equations. To quantify the uncertainty in the resulting individual cause-specific hazard rates, we further introduce a variational latent variable model. We show that our model exhibits state-of-the-art performance on popular survival data sets and demonstrate its efficacy in a multi-state setting.

Implicit Priors for Knowledge Sharing in Bayesian Neural Networks

Bayesian interpretations of neural network have a long history, dating back to early work in the 1990's and have recently regained attention because of their desirable properties like uncertainty estimation, model robustness and regularisation. We want to discuss here the application of Bayesian models to knowledge sharing between neural networks. Knowledge sharing comes in different facets, such as transfer learning, model distillation and shared embeddings. All of these tasks have in common that learned "features" ought to be shared across different networks. Theoretically rooted in the concepts of Bayesian neural networks this work has widespread application to general deep learning.

Bernoulli Race Particle Filters

When the weights in a particle filter are not available analytically, standard resampling methods cannot be employed. To circumvent this problem state-of-the-art algorithms replace the true weights with non-negative unbiased estimates. This algorithm is still valid but at the cost of higher variance of the resulting filtering estimates in comparison to a particle filter using the true weights. We propose here a novel algorithm that allows for resampling according to the true intractable weights when only an unbiased estimator of the weights is available. We demonstrate our algorithm on several examples.