Neural ODEs for Multi-State Survival Analysis

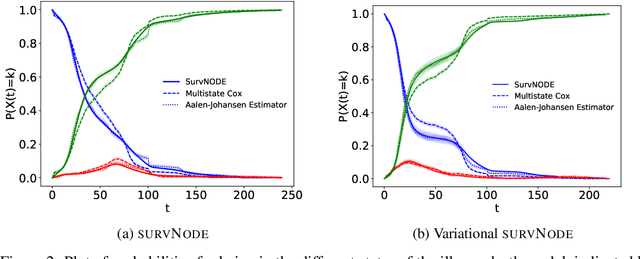
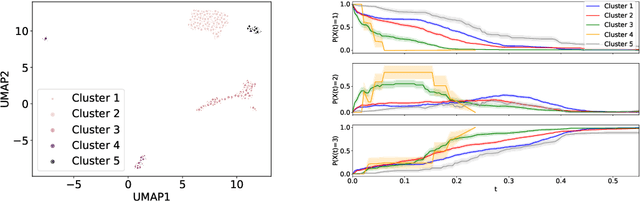
Survival models are a popular tool for the analysis of time to event data with applications in medicine, engineering, economics and many more. Advances like the Cox proportional hazard model have enabled researchers to better describe hazard rates for the occurrence of single fatal events, but are limited by modeling assumptions, like proportionality of hazard rates and linear effects. Moreover, common phenomena are often better described through multiple states, for example, the progress of a disease might be modeled as healthy, sick and dead instead of healthy and dead, where the competing nature of death and disease has to be taken into account. Also, individual characteristics can vary significantly between observational units, like patients, resulting in idiosyncratic hazard rates and different disease trajectories. These considerations require flexible modeling assumptions. Current standard models, however, are often ill-suited for such an analysis. To overcome these issues, we propose the use of neural ordinary differential equations as a flexible and general method for estimating multi-state survival models by directly solving the Kolmogorov forward equations. To quantify the uncertainty in the resulting individual cause-specific hazard rates, we further introduce a variational latent variable model. We show that our model exhibits state-of-the-art performance on popular survival data sets and demonstrate its efficacy in a multi-state setting.