Stefan Groha
SurvLatent ODE : A Neural ODE based time-to-event model with competing risks for longitudinal data improves cancer-associated Deep Vein Thrombosis prediction
Apr 20, 2022



Abstract:Effective learning from electronic health records (EHR) data for prediction of clinical outcomes is often challenging because of features recorded at irregular timesteps and loss to follow-up as well as competing events such as death or disease progression. To that end, we propose a generative time-to-event model, SurvLatent ODE, which adopts an Ordinary Differential Equation-based Recurrent Neural Networks (ODE-RNN) as an encoder to effectively parameterize a latent representation under irregularly sampled data. Our model then utilizes the latent representation to flexibly estimate survival times for multiple competing events without specifying shapes of event-specific hazard function. We demonstrate competitive performance of our model on MIMIC-III, a freely-available longitudinal dataset collected from critical care units, on predicting hospital mortality as well as the data from the Dana-Farber Cancer Institute (DFCI) on predicting onset of Deep Vein Thrombosis (DVT), a life-threatening complication for patients with cancer, with death as a competing event. SurvLatent ODE outperforms the current clinical standard Khorana Risk scores for stratifying DVT risk groups.
Topological Data Analysis of copy number alterations in cancer
Nov 22, 2020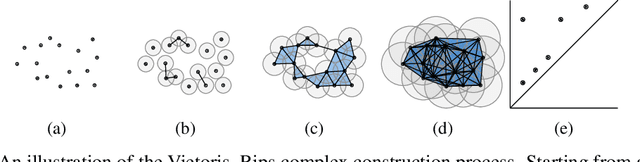



Abstract:Identifying subgroups and properties of cancer biopsy samples is a crucial step towards obtaining precise diagnoses and being able to perform personalized treatment of cancer patients. Recent data collections provide a comprehensive characterization of cancer cell data, including genetic data on copy number alterations (CNAs). We explore the potential to capture information contained in cancer genomic information using a novel topology-based approach that encodes each cancer sample as a persistence diagram of topological features, i.e., high-dimensional voids represented in the data. We find that this technique has the potential to extract meaningful low-dimensional representations in cancer somatic genetic data and demonstrate the viability of some applications on finding substructures in cancer data as well as comparing similarity of cancer types.
Neural ODEs for Multi-State Survival Analysis
Jun 08, 2020

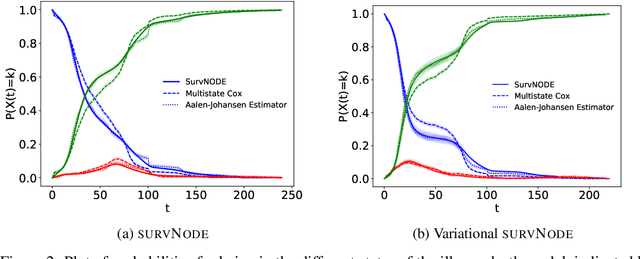
Abstract:Survival models are a popular tool for the analysis of time to event data with applications in medicine, engineering, economics and many more. Advances like the Cox proportional hazard model have enabled researchers to better describe hazard rates for the occurrence of single fatal events, but are limited by modeling assumptions, like proportionality of hazard rates and linear effects. Moreover, common phenomena are often better described through multiple states, for example, the progress of a disease might be modeled as healthy, sick and dead instead of healthy and dead, where the competing nature of death and disease has to be taken into account. Also, individual characteristics can vary significantly between observational units, like patients, resulting in idiosyncratic hazard rates and different disease trajectories. These considerations require flexible modeling assumptions. Current standard models, however, are often ill-suited for such an analysis. To overcome these issues, we propose the use of neural ordinary differential equations as a flexible and general method for estimating multi-state survival models by directly solving the Kolmogorov forward equations. To quantify the uncertainty in the resulting individual cause-specific hazard rates, we further introduce a variational latent variable model. We show that our model exhibits state-of-the-art performance on popular survival data sets and demonstrate its efficacy in a multi-state setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge