Learning-Rate-Free Stochastic Optimization over Riemannian Manifolds

In recent years, interest in gradient-based optimization over Riemannian manifolds has surged. However, a significant challenge lies in the reliance on hyperparameters, especially the learning rate, which requires meticulous tuning by practitioners to ensure convergence at a suitable rate. In this work, we introduce innovative learning-rate-free algorithms for stochastic optimization over Riemannian manifolds, eliminating the need for hand-tuning and providing a more robust and user-friendly approach. We establish high probability convergence guarantees that are optimal, up to logarithmic factors, compared to the best-known optimally tuned rate in the deterministic setting. Our approach is validated through numerical experiments, demonstrating competitive performance against learning-rate-dependent algorithms.

Markovian Flow Matching: Accelerating MCMC with Continuous Normalizing Flows

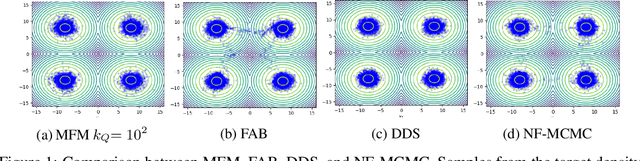
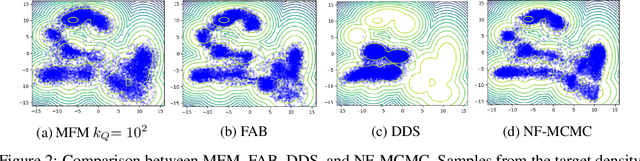
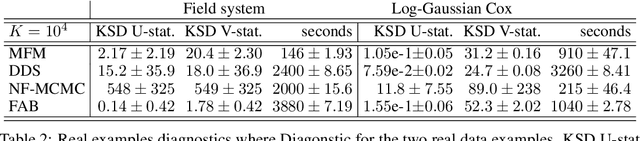
Continuous normalizing flows (CNFs) learn the probability path between a reference and a target density by modeling the vector field generating said path using neural networks. Recently, Lipman et al. (2022) introduced a simple and inexpensive method for training CNFs in generative modeling, termed flow matching (FM). In this paper, we re-purpose this method for probabilistic inference by incorporating Markovian sampling methods in evaluating the FM objective and using the learned probability path to improve Monte Carlo sampling. We propose a sequential method, which uses samples from a Markov chain to fix the probability path defining the FM objective. We augment this scheme with an adaptive tempering mechanism that allows the discovery of multiple modes in the target. Under mild assumptions, we establish convergence to a local optimum of the FM objective, discuss improvements in the convergence rate, and illustrate our methods on synthetic and real-world examples.

CoinEM: Tuning-Free Particle-Based Variational Inference for Latent Variable Models

We introduce two new particle-based algorithms for learning latent variable models via marginal maximum likelihood estimation, including one which is entirely tuning-free. Our methods are based on the perspective of marginal maximum likelihood estimation as an optimization problem: namely, as the minimization of a free energy functional. One way to solve this problem is to consider the discretization of a gradient flow associated with the free energy. We study one such approach, which resembles an extension of the popular Stein variational gradient descent algorithm. In particular, we establish a descent lemma for this algorithm, which guarantees that the free energy decreases at each iteration. This method, and any other obtained as the discretization of the gradient flow, will necessarily depend on a learning rate which must be carefully tuned by the practitioner in order to ensure convergence at a suitable rate. With this in mind, we also propose another algorithm for optimizing the free energy which is entirely learning rate free, based on coin betting techniques from convex optimization. We validate the performance of our algorithms across a broad range of numerical experiments, including several high-dimensional settings. Our results are competitive with existing particle-based methods, without the need for any hyperparameter tuning.

Learning Rate Free Bayesian Inference in Constrained Domains

We introduce a suite of new particle-based algorithms for sampling on constrained domains which are entirely learning rate free. Our approach leverages coin betting ideas from convex optimisation, and the viewpoint of constrained sampling as a mirrored optimisation problem on the space of probability measures. Based on this viewpoint, we also introduce a unifying framework for several existing constrained sampling algorithms, including mirrored Langevin dynamics and mirrored Stein variational gradient descent. We demonstrate the performance of our algorithms on a range of numerical examples, including sampling from targets on the simplex, sampling with fairness constraints, and constrained sampling problems in post-selection inference. Our results indicate that our algorithms achieve competitive performance with existing constrained sampling methods, without the need to tune any hyperparameters.

Coin Sampling: Gradient-Based Bayesian Inference without Learning Rates

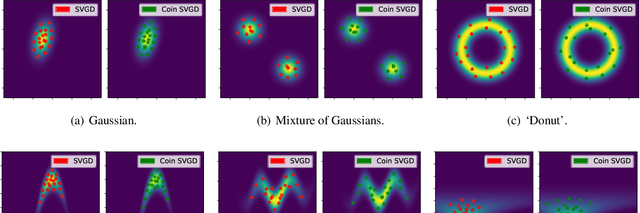
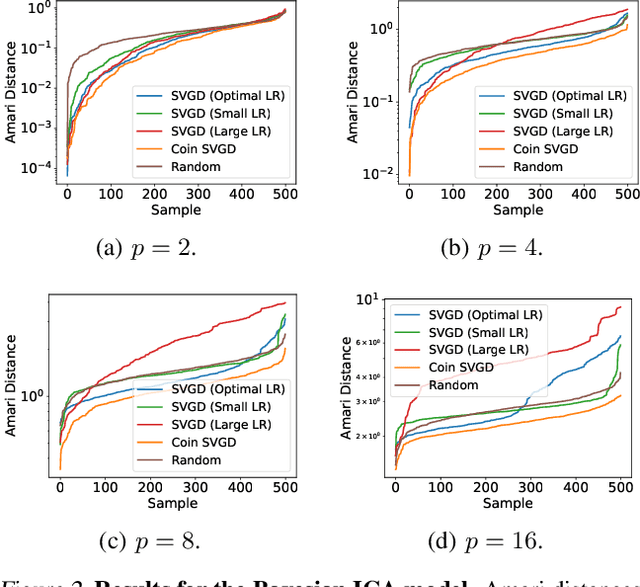
In recent years, particle-based variational inference (ParVI) methods such as Stein variational gradient descent (SVGD) have grown in popularity as scalable methods for Bayesian inference. Unfortunately, the properties of such methods invariably depend on hyperparameters such as the learning rate, which must be carefully tuned by the practitioner in order to ensure convergence to the target measure at a suitable rate. In this paper, we introduce a suite of new particle-based methods for scalable Bayesian inference based on coin betting, which are entirely learning-rate free. We illustrate the performance of our approach on a range of numerical examples, including several high-dimensional models and datasets, demonstrating comparable performance to other ParVI algorithms.

Sequential Neural Score Estimation: Likelihood-Free Inference with Conditional Score Based Diffusion Models

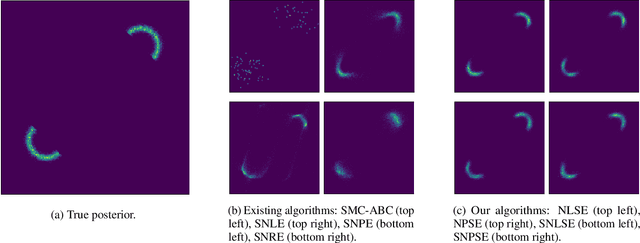
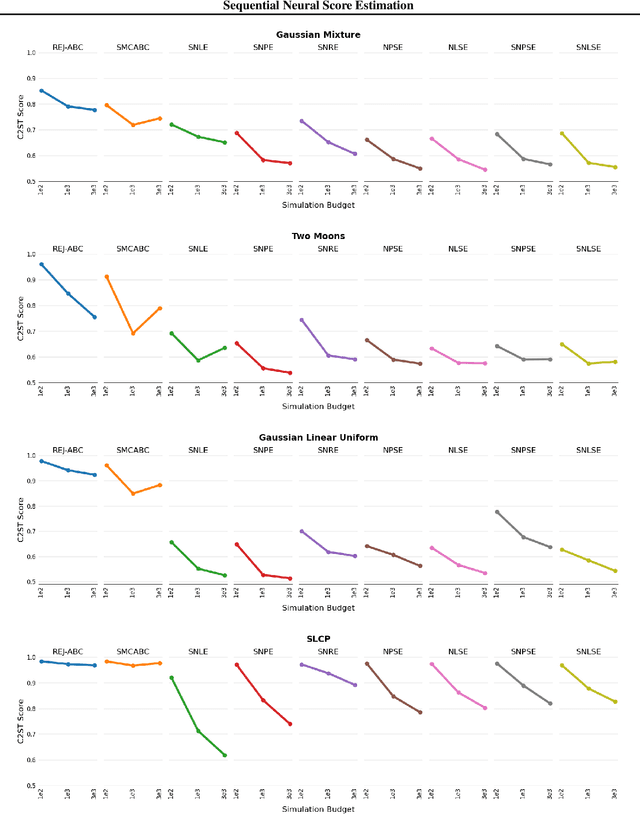
We introduce Sequential Neural Posterior Score Estimation (SNPSE) and Sequential Neural Likelihood Score Estimation (SNLSE), two new score-based methods for Bayesian inference in simulator-based models. Our methods, inspired by the success of score-based methods in generative modelling, leverage conditional score-based diffusion models to generate samples from the posterior distribution of interest. These models can be trained using one of two possible objective functions, one of which approximates the score of the intractable likelihood, while the other directly estimates the score of the posterior. We embed these models into a sequential training procedure, which guides simulations using the current approximation of the posterior at the observation of interest, thereby reducing the simulation cost. We validate our methods, as well as their amortised, non-sequential variants, on several numerical examples, demonstrating comparable or superior performance to existing state-of-the-art methods such as Sequential Neural Posterior Estimation (SNPE) and Sequential Neural Likelihood Estimation (SNLE).

Two-Timescale Stochastic Approximation for Bilevel Optimisation Problems in Continuous-Time Models

We analyse the asymptotic properties of a continuous-time, two-timescale stochastic approximation algorithm designed for stochastic bilevel optimisation problems in continuous-time models. We obtain the weak convergence rate of this algorithm in the form of a central limit theorem. We also demonstrate how this algorithm can be applied to several continuous-time bilevel optimisation problems.

F-Divergences and Cost Function Locality in Generative Modelling with Quantum Circuits

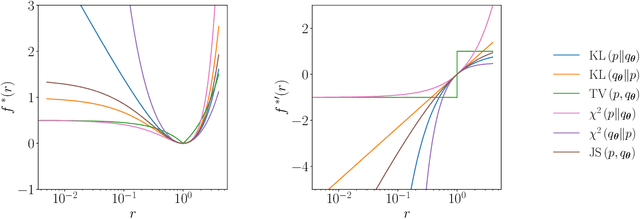
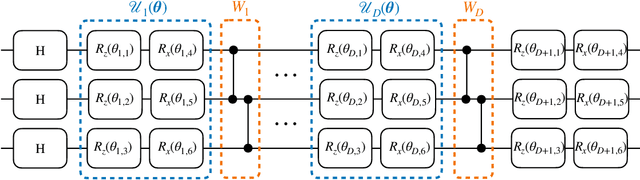
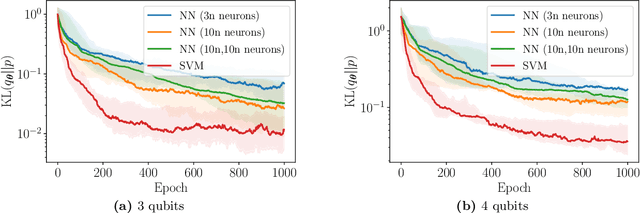
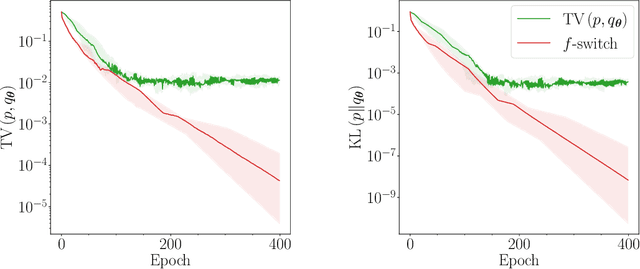
Generative modelling is an important unsupervised task in machine learning. In this work, we study a hybrid quantum-classical approach to this task, based on the use of a quantum circuit Born machine. In particular, we consider training a quantum circuit Born machine using $f$-divergences. We first discuss the adversarial framework for generative modelling, which enables the estimation of any $f$-divergence in the near term. Based on this capability, we introduce two heuristics which demonstrably improve the training of the Born machine. The first is based on $f$-divergence switching during training. The second introduces locality to the divergence, a strategy which has proved important in similar applications in terms of mitigating barren plateaus. Finally, we discuss the long-term implications of quantum devices for computing $f$-divergences, including algorithms which provide quadratic speedups to their estimation. In particular, we generalise existing algorithms for estimating the Kullback-Leibler divergence and the total variation distance to obtain a fault-tolerant quantum algorithm for estimating another $f$-divergence, namely, the Pearson divergence.