Learning Rate Free Bayesian Inference in Constrained Domains

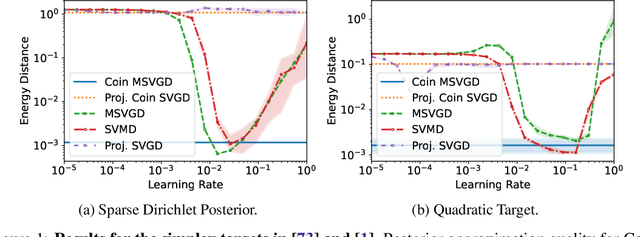
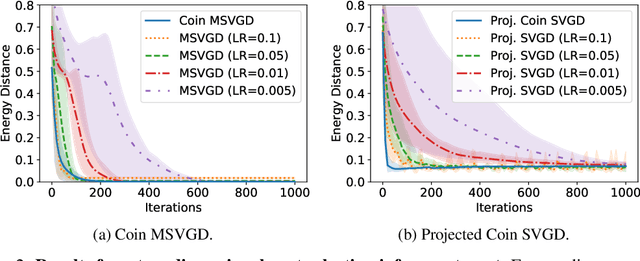
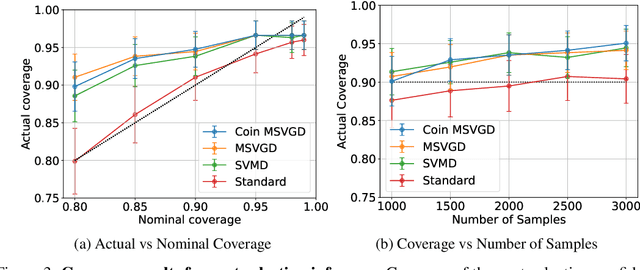
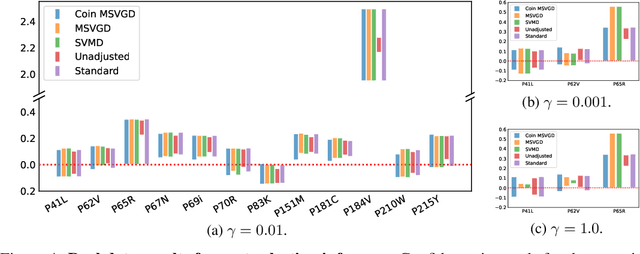
We introduce a suite of new particle-based algorithms for sampling on constrained domains which are entirely learning rate free. Our approach leverages coin betting ideas from convex optimisation, and the viewpoint of constrained sampling as a mirrored optimisation problem on the space of probability measures. Based on this viewpoint, we also introduce a unifying framework for several existing constrained sampling algorithms, including mirrored Langevin dynamics and mirrored Stein variational gradient descent. We demonstrate the performance of our algorithms on a range of numerical examples, including sampling from targets on the simplex, sampling with fairness constraints, and constrained sampling problems in post-selection inference. Our results indicate that our algorithms achieve competitive performance with existing constrained sampling methods, without the need to tune any hyperparameters.