Markovian Flow Matching: Accelerating MCMC with Continuous Normalizing Flows
Paper and Code
May 23, 2024
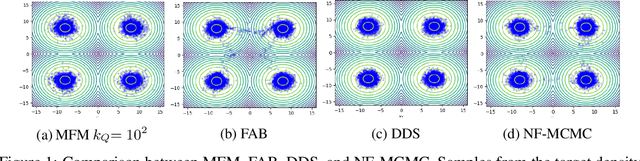
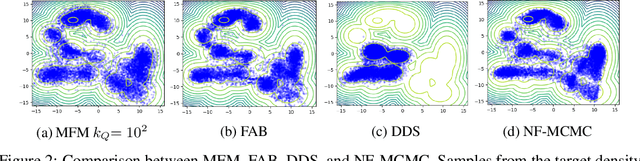
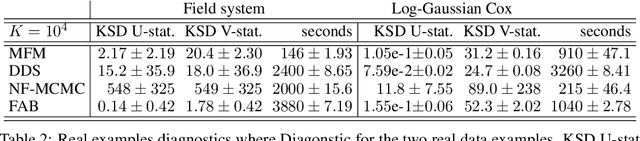
Continuous normalizing flows (CNFs) learn the probability path between a reference and a target density by modeling the vector field generating said path using neural networks. Recently, Lipman et al. (2022) introduced a simple and inexpensive method for training CNFs in generative modeling, termed flow matching (FM). In this paper, we re-purpose this method for probabilistic inference by incorporating Markovian sampling methods in evaluating the FM objective and using the learned probability path to improve Monte Carlo sampling. We propose a sequential method, which uses samples from a Markov chain to fix the probability path defining the FM objective. We augment this scheme with an adaptive tempering mechanism that allows the discovery of multiple modes in the target. Under mild assumptions, we establish convergence to a local optimum of the FM objective, discuss improvements in the convergence rate, and illustrate our methods on synthetic and real-world examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge