F-Divergences and Cost Function Locality in Generative Modelling with Quantum Circuits
Paper and Code
Oct 08, 2021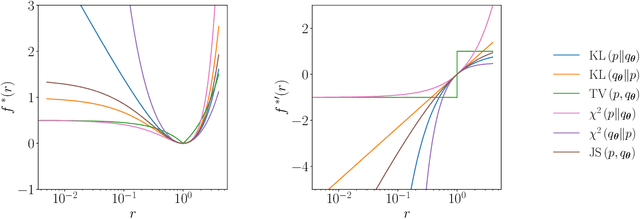
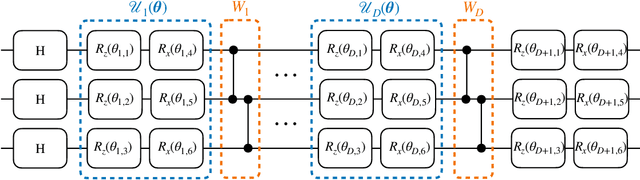
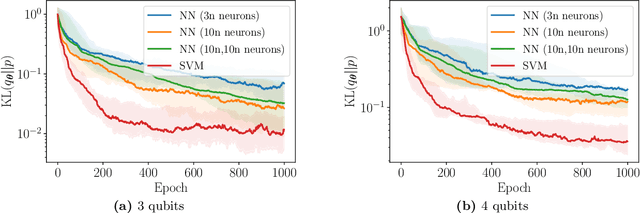
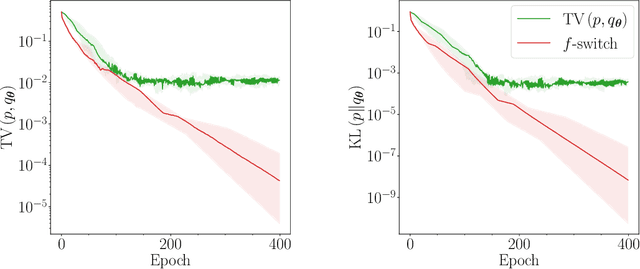
Generative modelling is an important unsupervised task in machine learning. In this work, we study a hybrid quantum-classical approach to this task, based on the use of a quantum circuit Born machine. In particular, we consider training a quantum circuit Born machine using $f$-divergences. We first discuss the adversarial framework for generative modelling, which enables the estimation of any $f$-divergence in the near term. Based on this capability, we introduce two heuristics which demonstrably improve the training of the Born machine. The first is based on $f$-divergence switching during training. The second introduces locality to the divergence, a strategy which has proved important in similar applications in terms of mitigating barren plateaus. Finally, we discuss the long-term implications of quantum devices for computing $f$-divergences, including algorithms which provide quadratic speedups to their estimation. In particular, we generalise existing algorithms for estimating the Kullback-Leibler divergence and the total variation distance to obtain a fault-tolerant quantum algorithm for estimating another $f$-divergence, namely, the Pearson divergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge