Training-efficient density quantum machine learning

Quantum machine learning requires powerful, flexible and efficiently trainable models to be successful in solving challenging problems. In this work, we present density quantum neural networks, a learning model incorporating randomisation over a set of trainable unitaries. These models generalise quantum neural networks using parameterised quantum circuits, and allow a trade-off between expressibility and efficient trainability, particularly on quantum hardware. We demonstrate the flexibility of the formalism by applying it to two recently proposed model families. The first are commuting-block quantum neural networks (QNNs) which are efficiently trainable but may be limited in expressibility. The second are orthogonal (Hamming-weight preserving) quantum neural networks which provide well-defined and interpretable transformations on data but are challenging to train at scale on quantum devices. Density commuting QNNs improve capacity with minimal gradient complexity overhead, and density orthogonal neural networks admit a quadratic-to-constant gradient query advantage with minimal to no performance loss. We conduct numerical experiments on synthetic translationally invariant data and MNIST image data with hyperparameter optimisation to support our findings. Finally, we discuss the connection to post-variational quantum neural networks, measurement-based quantum machine learning and the dropout mechanism.

Machine learning applications for noisy intermediate-scale quantum computers

Quantum machine learning has proven to be a fruitful area in which to search for potential applications of quantum computers. This is particularly true for those available in the near term, so called noisy intermediate-scale quantum (NISQ) devices. In this Thesis, we develop and study three quantum machine learning applications suitable for NISQ computers, ordered in terms of increasing complexity of data presented to them. These algorithms are variational in nature and use parameterised quantum circuits (PQCs) as the underlying quantum machine learning model. The first application area is quantum classification using PQCs, where the data is classical feature vectors and their corresponding labels. Here, we study the robustness of certain data encoding strategies in such models against noise present in a quantum computer. The second area is generative modelling using quantum computers, where we use quantum circuit Born machines to learn and sample from complex probability distributions. We discuss and present a framework for quantum advantage for such models, propose gradient-based training methods and demonstrate these both numerically and on the Rigetti quantum computer up to 28 qubits. For our final application, we propose a variational algorithm in the area of approximate quantum cloning, where the data becomes quantum in nature. For the algorithm, we derive differentiable cost functions, prove theoretical guarantees such as faithfulness, and incorporate state of the art methods such as quantum architecture search. Furthermore, we demonstrate how this algorithm is useful in discovering novel implementable attacks on quantum cryptographic protocols, focusing on quantum coin flipping and key distribution as examples.

Graph neural network initialisation of quantum approximate optimisation

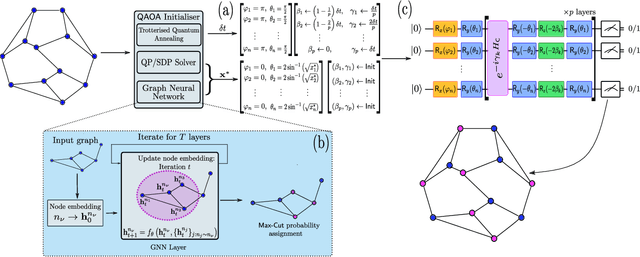
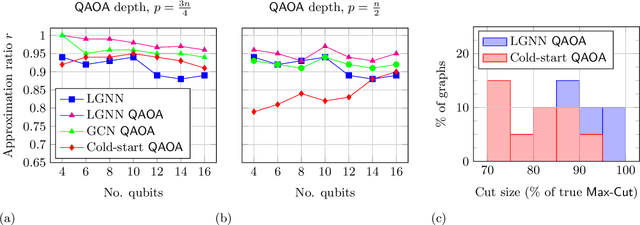
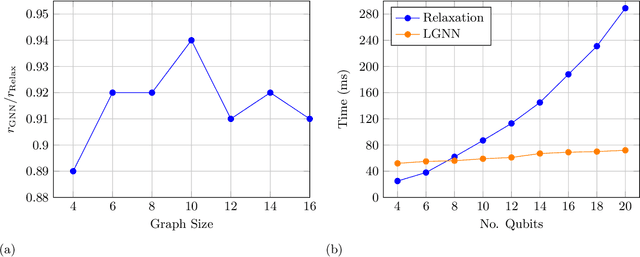
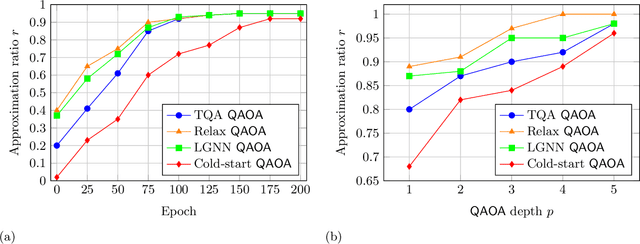
Approximate combinatorial optimisation has emerged as one of the most promising application areas for quantum computers, particularly those in the near term. In this work, we focus on the quantum approximate optimisation algorithm (QAOA) for solving the Max-Cut problem. Specifically, we address two problems in the QAOA, how to select initial parameters, and how to subsequently train the parameters to find an optimal solution. For the former, we propose graph neural networks (GNNs) as an initialisation routine for the QAOA parameters, adding to the literature on warm-starting techniques. We show the GNN approach generalises across not only graph instances, but also to increasing graph sizes, a feature not available to other warm-starting techniques. For training the QAOA, we test several optimisers for the MaxCut problem. These include quantum aware/agnostic optimisers proposed in literature and we also incorporate machine learning techniques such as reinforcement and meta-learning. With the incorporation of these initialisation and optimisation toolkits, we demonstrate how the QAOA can be trained as an end-to-end differentiable pipeline.

F-Divergences and Cost Function Locality in Generative Modelling with Quantum Circuits

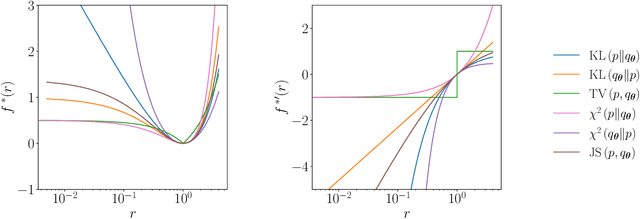
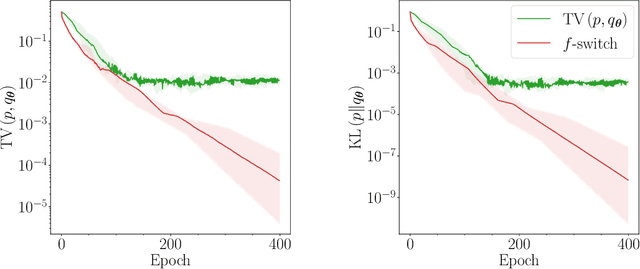
Generative modelling is an important unsupervised task in machine learning. In this work, we study a hybrid quantum-classical approach to this task, based on the use of a quantum circuit Born machine. In particular, we consider training a quantum circuit Born machine using $f$-divergences. We first discuss the adversarial framework for generative modelling, which enables the estimation of any $f$-divergence in the near term. Based on this capability, we introduce two heuristics which demonstrably improve the training of the Born machine. The first is based on $f$-divergence switching during training. The second introduces locality to the divergence, a strategy which has proved important in similar applications in terms of mitigating barren plateaus. Finally, we discuss the long-term implications of quantum devices for computing $f$-divergences, including algorithms which provide quadratic speedups to their estimation. In particular, we generalise existing algorithms for estimating the Kullback-Leibler divergence and the total variation distance to obtain a fault-tolerant quantum algorithm for estimating another $f$-divergence, namely, the Pearson divergence.

Variational inference with a quantum computer

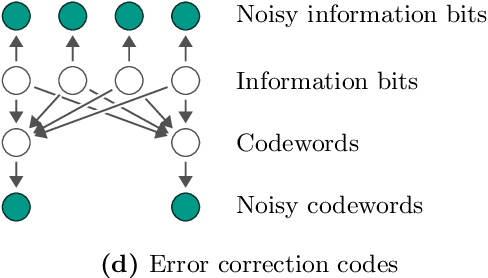
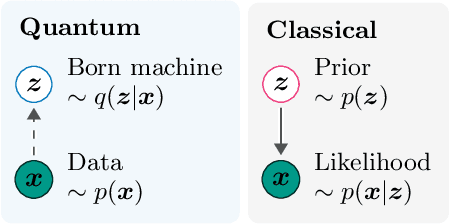
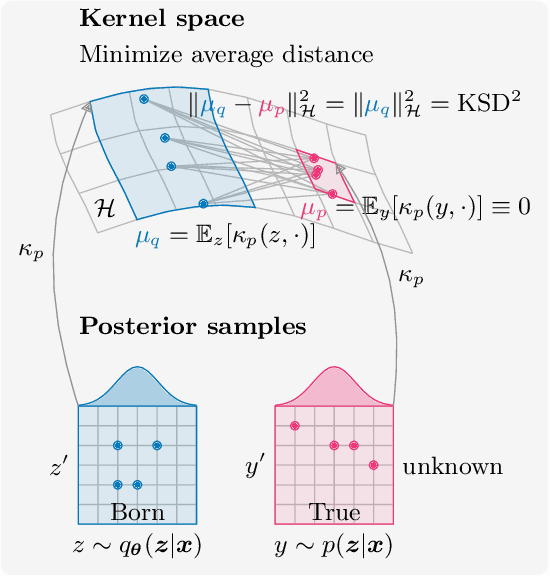
Inference is the task of drawing conclusions about unobserved variables given observations of related variables. Applications range from identifying diseases from symptoms to classifying economic regimes from price movements. Unfortunately, performing exact inference is intractable in general. One alternative is variational inference, where a candidate probability distribution is optimized to approximate the posterior distribution over unobserved variables. For good approximations a flexible and highly expressive candidate distribution is desirable. In this work, we propose quantum Born machines as variational distributions over discrete variables. We apply the framework of operator variational inference to achieve this goal. In particular, we adopt two specific realizations: one with an adversarial objective and one based on the kernelized Stein discrepancy. We demonstrate the approach numerically using examples of Bayesian networks, and implement an experiment on an IBM quantum computer. Our techniques enable efficient variational inference with distributions beyond those that are efficiently representable on a classical computer.

Variational Quantum Cloning: Improving Practicality for Quantum Cryptanalysis

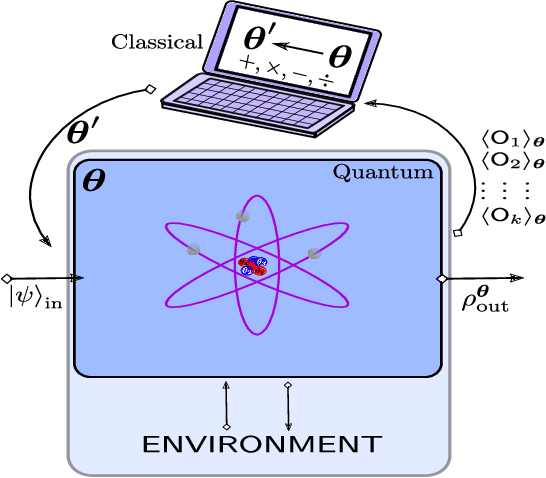
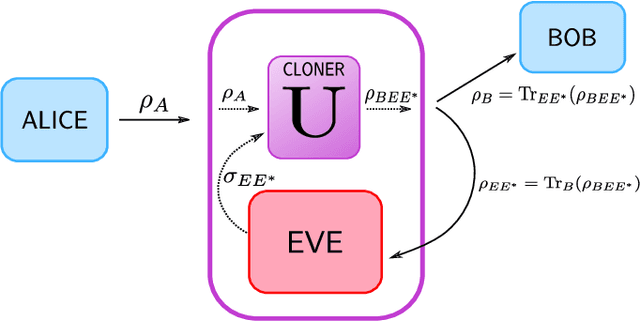
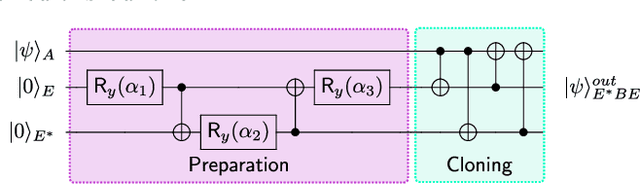
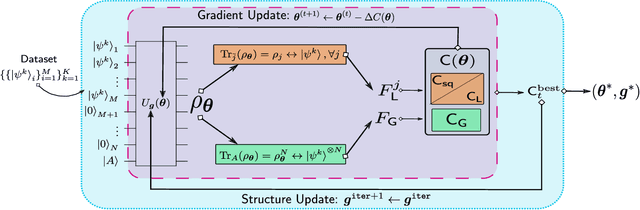
Cryptanalysis on standard quantum cryptographic systems generally involves finding optimal adversarial attack strategies on the underlying protocols. The core principle of modelling quantum attacks in many cases reduces to the adversary's ability to clone unknown quantum states which facilitates the extraction of some meaningful secret information. Explicit optimal attack strategies typically require high computational resources due to large circuit depths or, in many cases, are unknown. In this work, we propose variational quantum cloning (VQC), a quantum machine learning based cryptanalysis algorithm which allows an adversary to obtain optimal (approximate) cloning strategies with short depth quantum circuits, trained using hybrid classical-quantum techniques. The algorithm contains operationally meaningful cost functions with theoretical guarantees, quantum circuit structure learning and gradient descent based optimisation. Our approach enables the end-to-end discovery of hardware efficient quantum circuits to clone specific families of quantum states, which in turn leads to an improvement in cloning fidelites when implemented on quantum hardware: the Rigetti Aspen chip. Finally, we connect these results to quantum cryptographic primitives, in particular quantum coin flipping. We derive attacks on two protocols as examples, based on quantum cloning and facilitated by VQC. As a result, our algorithm can improve near term attacks on these protocols, using approximate quantum cloning as a resource.

Quantum versus Classical Generative Modelling in Finance

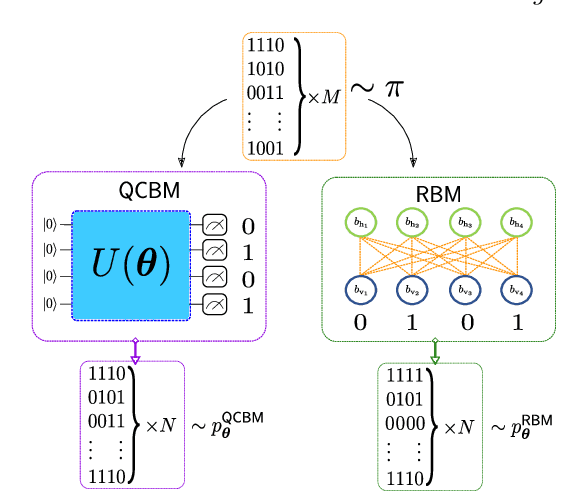
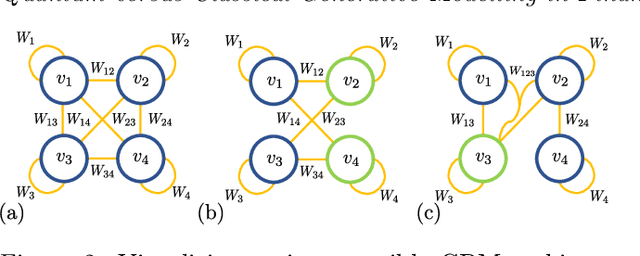
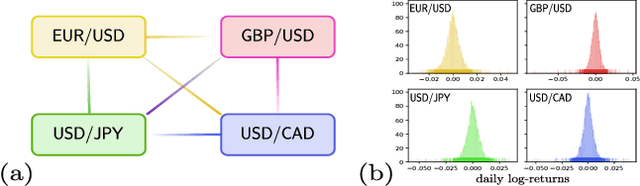
Finding a concrete use case for quantum computers in the near term is still an open question, with machine learning typically touted as one of the first fields which will be impacted by quantum technologies. In this work, we investigate and compare the capabilities of quantum versus classical models for the task of generative modelling in machine learning. We use a real world financial dataset consisting of correlated currency pairs and compare two models in their ability to learn the resulting distribution - a restricted Boltzmann machine, and a quantum circuit Born machine. We provide extensive numerical results indicating that the simulated Born machine always at least matches the performance of the Boltzmann machine in this task, and demonstrates superior performance as the model scales. We perform experiments on both simulated and physical quantum chips using the Rigetti forest platform, and also are able to partially train the largest instance to date of a quantum circuit Born machine on quantum hardware. Finally, by studying the entanglement capacity of the training Born machines, we find that entanglement typically plays a role in the problem instances which demonstrate an advantage over the Boltzmann machine.

Robust data encodings for quantum classifiers

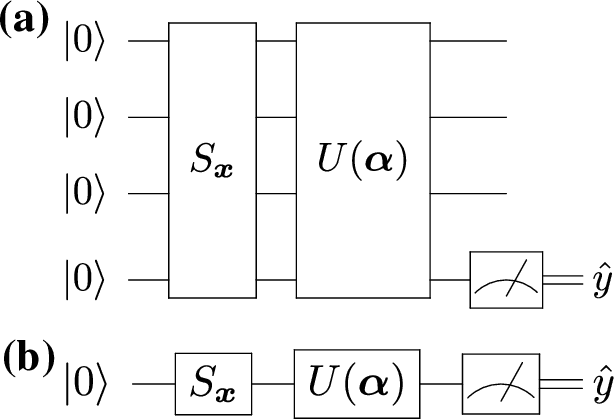
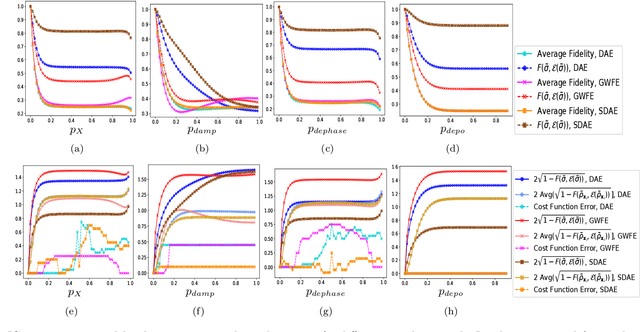
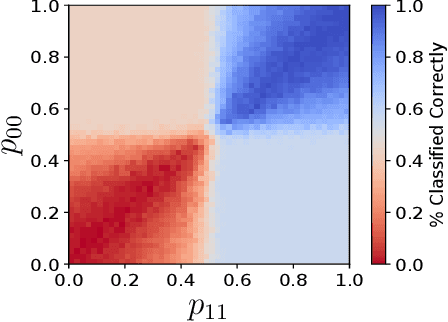
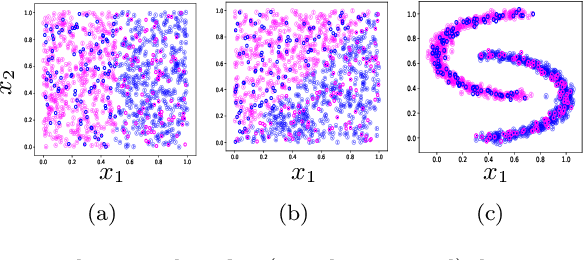
Data representation is crucial for the success of machine learning models. In the context of quantum machine learning with near-term quantum computers, equally important considerations of how to efficiently input (encode) data and effectively deal with noise arise. In this work, we study data encodings for binary quantum classification and investigate their properties both with and without noise. For the common classifier we consider, we show that encodings determine the classes of learnable decision boundaries as well as the set of points which retain the same classification in the presence of noise. After defining the notion of a robust data encoding, we prove several results on robustness for different channels, discuss the existence of robust encodings, and prove an upper bound on the number of robust points in terms of fidelities between noisy and noiseless states. Numerical results for several example implementations are provided to reinforce our findings.

The Born Supremacy: Quantum Advantage and Training of an Ising Born Machine

The search for an application of near-term quantum devices is widespread. Quantum Machine Learning is touted as a potential utilisation of such devices, particularly those which are out of the reach of the simulation capabilities of classical computers. In this work, we propose a generative Quantum Machine Learning Model, called the Ising Born Machine (IBM), which we show cannot, in the worst case, and up to suitable notions of error, be simulated efficiently by a classical device. We also show this holds for all the circuit families encountered during training. In particular, we explore quantum circuit learning using non-universal circuits derived from Ising Model Hamiltonians, which are implementable on near term quantum devices. We propose two novel training methods for the IBM by utilising the Stein Discrepancy and the Sinkhorn Divergence cost functions. We show numerically, both using a simulator within Rigetti's Forest platform and on the Aspen-1 16Q chip, that the cost functions we suggest outperform the more commonly used Maximum Mean Discrepancy (MMD) for differentiable training. We also propose an improvement to the MMD by proposing a novel utilisation of quantum kernels which we demonstrate provides improvements over its classical counterpart. We discuss the potential of these methods to learn `hard' quantum distributions, a feat which would demonstrate the advantage of quantum over classical computers, and provide the first formal definitions for what we call `Quantum Learning Supremacy'. Finally, we propose a novel view on the area of quantum circuit compilation by using the IBM to `mimic' target quantum circuits using classical output data only.