Ryan LaRose
Robust data encodings for quantum classifiers
Mar 03, 2020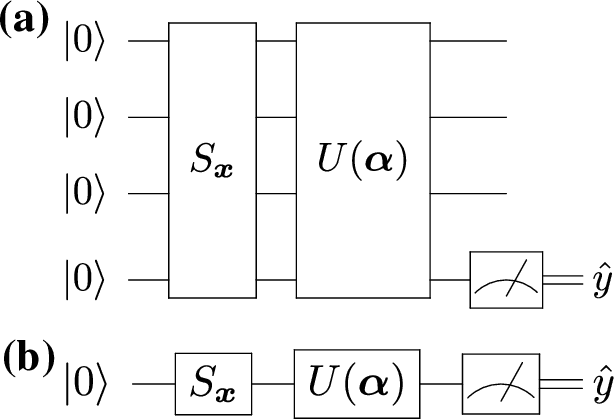
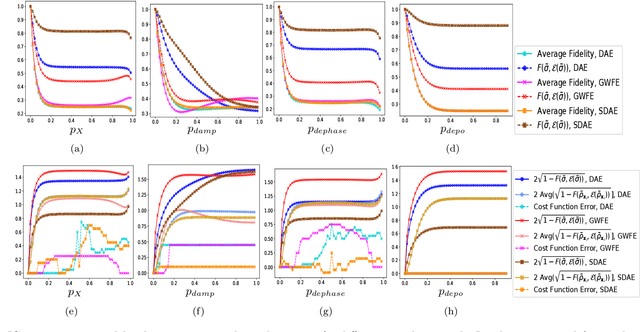
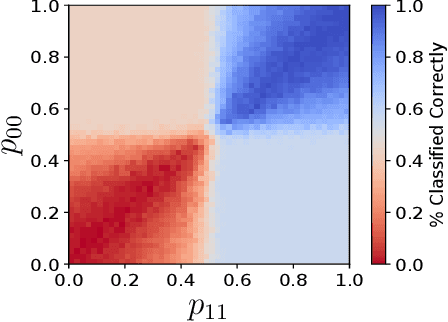
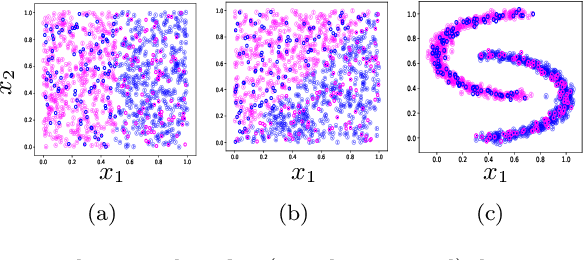
Abstract:Data representation is crucial for the success of machine learning models. In the context of quantum machine learning with near-term quantum computers, equally important considerations of how to efficiently input (encode) data and effectively deal with noise arise. In this work, we study data encodings for binary quantum classification and investigate their properties both with and without noise. For the common classifier we consider, we show that encodings determine the classes of learnable decision boundaries as well as the set of points which retain the same classification in the presence of noise. After defining the notion of a robust data encoding, we prove several results on robustness for different channels, discuss the existence of robust encodings, and prove an upper bound on the number of robust points in terms of fidelities between noisy and noiseless states. Numerical results for several example implementations are provided to reinforce our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge