Bayesian Learning of Parameterised Quantum Circuits

Currently available quantum computers suffer from constraints including hardware noise and a limited number of qubits. As such, variational quantum algorithms that utilise a classical optimiser in order to train a parameterised quantum circuit have drawn significant attention for near-term practical applications of quantum technology. In this work, we take a probabilistic point of view and reformulate the classical optimisation as an approximation of a Bayesian posterior. The posterior is induced by combining the cost function to be minimised with a prior distribution over the parameters of the quantum circuit. We describe a dimension reduction strategy based on a maximum a posteriori point estimate with a Laplace prior. Experiments on the Quantinuum H1-2 computer show that the resulting circuits are faster to execute and less noisy than the circuits trained without the dimension reduction strategy. We subsequently describe a posterior sampling strategy based on stochastic gradient Langevin dynamics. Numerical simulations on three different problems show that the strategy is capable of generating samples from the full posterior and avoiding local optima.

F-Divergences and Cost Function Locality in Generative Modelling with Quantum Circuits

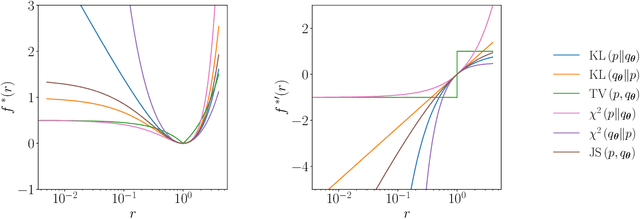
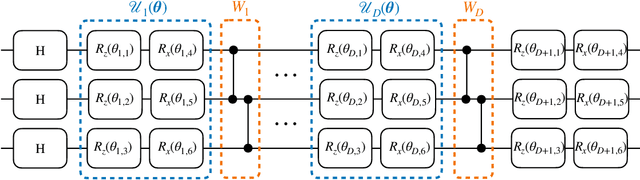
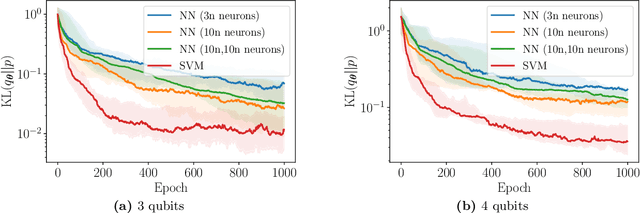
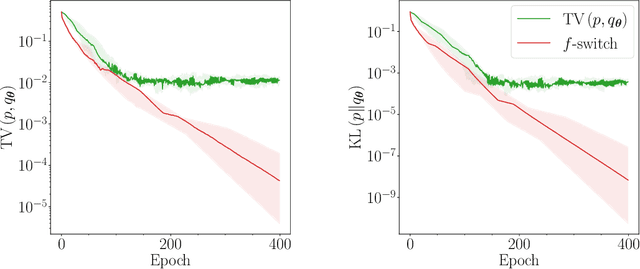
Generative modelling is an important unsupervised task in machine learning. In this work, we study a hybrid quantum-classical approach to this task, based on the use of a quantum circuit Born machine. In particular, we consider training a quantum circuit Born machine using $f$-divergences. We first discuss the adversarial framework for generative modelling, which enables the estimation of any $f$-divergence in the near term. Based on this capability, we introduce two heuristics which demonstrably improve the training of the Born machine. The first is based on $f$-divergence switching during training. The second introduces locality to the divergence, a strategy which has proved important in similar applications in terms of mitigating barren plateaus. Finally, we discuss the long-term implications of quantum devices for computing $f$-divergences, including algorithms which provide quadratic speedups to their estimation. In particular, we generalise existing algorithms for estimating the Kullback-Leibler divergence and the total variation distance to obtain a fault-tolerant quantum algorithm for estimating another $f$-divergence, namely, the Pearson divergence.

Variational inference with a quantum computer

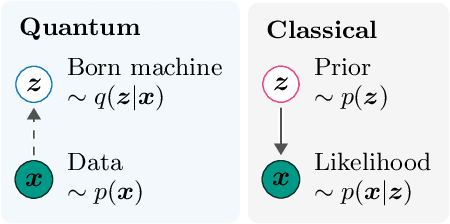
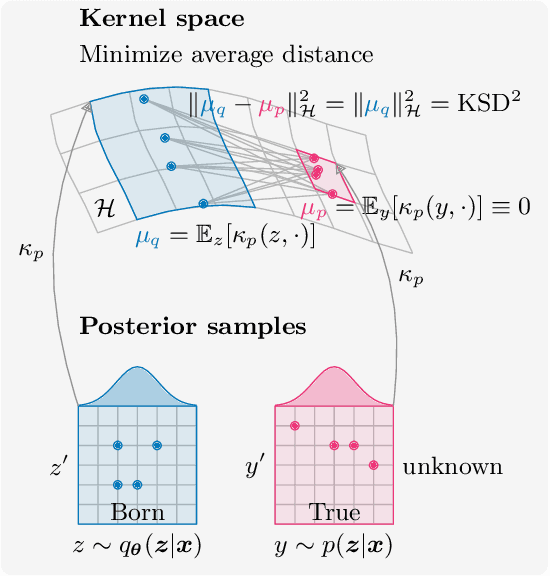
Inference is the task of drawing conclusions about unobserved variables given observations of related variables. Applications range from identifying diseases from symptoms to classifying economic regimes from price movements. Unfortunately, performing exact inference is intractable in general. One alternative is variational inference, where a candidate probability distribution is optimized to approximate the posterior distribution over unobserved variables. For good approximations a flexible and highly expressive candidate distribution is desirable. In this work, we propose quantum Born machines as variational distributions over discrete variables. We apply the framework of operator variational inference to achieve this goal. In particular, we adopt two specific realizations: one with an adversarial objective and one based on the kernelized Stein discrepancy. We demonstrate the approach numerically using examples of Bayesian networks, and implement an experiment on an IBM quantum computer. Our techniques enable efficient variational inference with distributions beyond those that are efficiently representable on a classical computer.

Parameterized quantum circuits as machine learning models

Hybrid quantum-classical systems make it possible to utilize existing quantum computers to their fullest extent. Within this framework, parameterized quantum circuits can be thought of as machine learning models with remarkable expressive power. This Review presents components of these models and discusses their application to a variety of data-driven tasks such as supervised learning and generative modeling. With experimental demonstrations carried out on actual quantum hardware, and with software actively being developed, this rapidly growing field could become one of the first instances of quantum computing that addresses real world problems.

Adversarial quantum circuit learning for pure state approximation

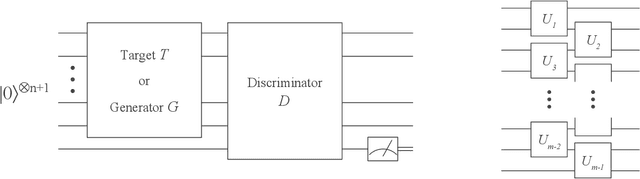
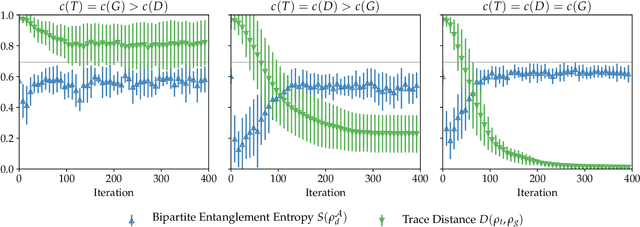
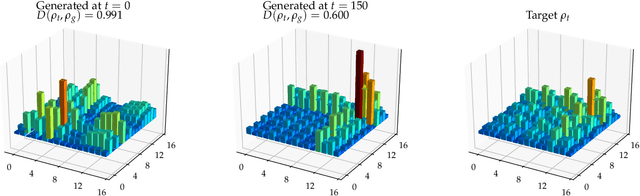
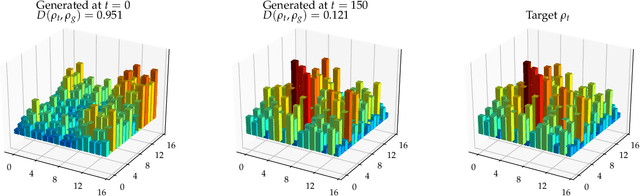
Adversarial learning is one of the most successful approaches to modelling high-dimensional probability distributions from data. The quantum computing community has recently begun to generalise this idea and to look for potential applications. In this work, we derive an adversarial algorithm for the problem of approximating an unknown quantum pure state. Although this could be done on universal quantum computers, the adversarial formulation enables us to execute the algorithm on near-term quantum computers. Two parametrized circuits are optimized in tandem: One tries to approximate the target state, the other tries to distinguish between target and approximated state. Supported by numerical simulations, we show that resilient backpropagation algorithms perform remarkably well in optimizing the two circuits. We use the bipartite entanglement entropy to design an efficient heuristic for the stopping criterion. Our approach may find application in quantum state tomography.

Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models

Mainstream machine-learning techniques such as deep learning and probabilistic programming rely heavily on sampling from generally intractable probability distributions. There is increasing interest in the potential advantages of using quantum computing technologies as sampling engines to speed up these tasks or to make them more effective. However, some pressing challenges in state-of-the-art quantum annealers have to be overcome before we can assess their actual performance. The sparse connectivity, resulting from the local interaction between quantum bits in physical hardware implementations, is considered the most severe limitation to the quality of constructing powerful generative unsupervised machine-learning models. Here we use embedding techniques to add redundancy to data sets, allowing us to increase the modeling capacity of quantum annealers. We illustrate our findings by training hardware-embedded graphical models on a binarized data set of handwritten digits and two synthetic data sets in experiments with up to 940 quantum bits. Our model can be trained in quantum hardware without full knowledge of the effective parameters specifying the corresponding quantum Gibbs-like distribution; therefore, this approach avoids the need to infer the effective temperature at each iteration, speeding up learning; it also mitigates the effect of noise in the control parameters, making it robust to deviations from the reference Gibbs distribution. Our approach demonstrates the feasibility of using quantum annealers for implementing generative models, and it provides a suitable framework for benchmarking these quantum technologies on machine-learning-related tasks.