Bayesian Learning of Parameterised Quantum Circuits

Currently available quantum computers suffer from constraints including hardware noise and a limited number of qubits. As such, variational quantum algorithms that utilise a classical optimiser in order to train a parameterised quantum circuit have drawn significant attention for near-term practical applications of quantum technology. In this work, we take a probabilistic point of view and reformulate the classical optimisation as an approximation of a Bayesian posterior. The posterior is induced by combining the cost function to be minimised with a prior distribution over the parameters of the quantum circuit. We describe a dimension reduction strategy based on a maximum a posteriori point estimate with a Laplace prior. Experiments on the Quantinuum H1-2 computer show that the resulting circuits are faster to execute and less noisy than the circuits trained without the dimension reduction strategy. We subsequently describe a posterior sampling strategy based on stochastic gradient Langevin dynamics. Numerical simulations on three different problems show that the strategy is capable of generating samples from the full posterior and avoiding local optima.

Variational inference with a quantum computer

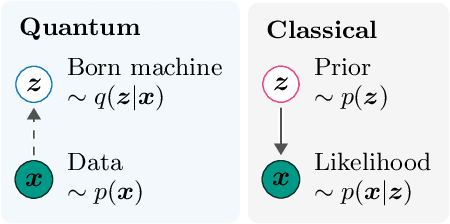
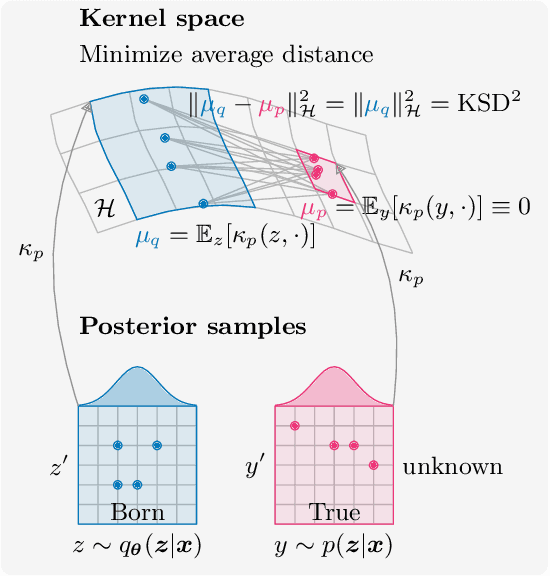
Inference is the task of drawing conclusions about unobserved variables given observations of related variables. Applications range from identifying diseases from symptoms to classifying economic regimes from price movements. Unfortunately, performing exact inference is intractable in general. One alternative is variational inference, where a candidate probability distribution is optimized to approximate the posterior distribution over unobserved variables. For good approximations a flexible and highly expressive candidate distribution is desirable. In this work, we propose quantum Born machines as variational distributions over discrete variables. We apply the framework of operator variational inference to achieve this goal. In particular, we adopt two specific realizations: one with an adversarial objective and one based on the kernelized Stein discrepancy. We demonstrate the approach numerically using examples of Bayesian networks, and implement an experiment on an IBM quantum computer. Our techniques enable efficient variational inference with distributions beyond those that are efficiently representable on a classical computer.