Generative Learning of Continuous Data by Tensor Networks

Beyond their origin in modeling many-body quantum systems, tensor networks have emerged as a promising class of models for solving machine learning problems, notably in unsupervised generative learning. While possessing many desirable features arising from their quantum-inspired nature, tensor network generative models have previously been largely restricted to binary or categorical data, limiting their utility in real-world modeling problems. We overcome this by introducing a new family of tensor network generative models for continuous data, which are capable of learning from distributions containing continuous random variables. We develop our method in the setting of matrix product states, first deriving a universal expressivity theorem proving the ability of this model family to approximate any reasonably smooth probability density function with arbitrary precision. We then benchmark the performance of this model on several synthetic and real-world datasets, finding that the model learns and generalizes well on distributions of continuous and discrete variables. We develop methods for modeling different data domains, and introduce a trainable compression layer which is found to increase model performance given limited memory or computational resources. Overall, our methods give important theoretical and empirical evidence of the efficacy of quantum-inspired methods for the rapidly growing field of generative learning.

A Framework for Demonstrating Practical Quantum Advantage: Racing Quantum against Classical Generative Models

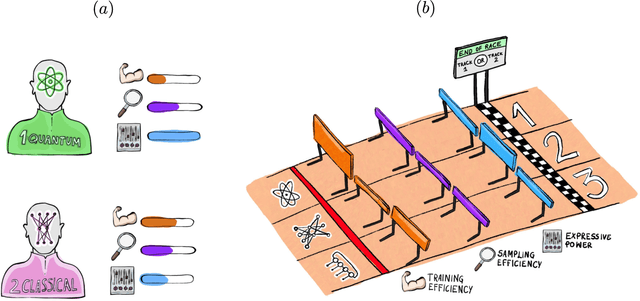
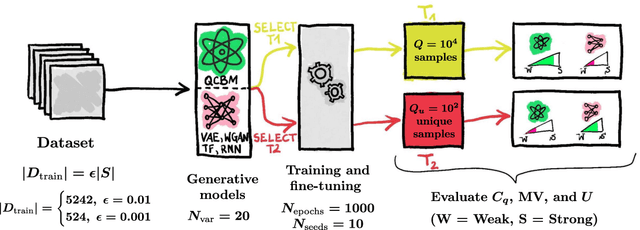
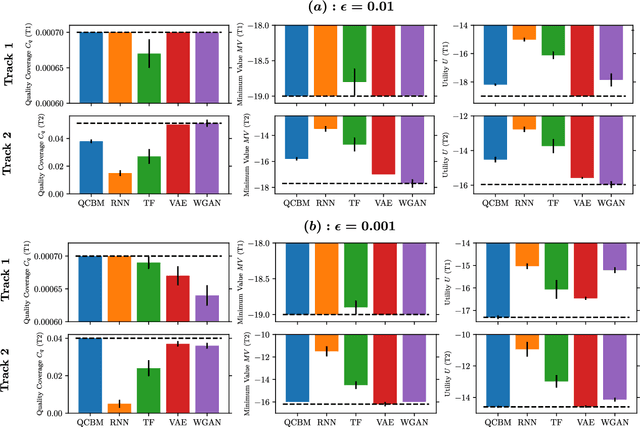
Generative modeling has seen a rising interest in both classical and quantum machine learning, and it represents a promising candidate to obtain a practical quantum advantage in the near term. In this study, we build over a proposed framework for evaluating the generalization performance of generative models, and we establish the first quantitative comparative race towards practical quantum advantage (PQA) between classical and quantum generative models, namely Quantum Circuit Born Machines (QCBMs), Transformers (TFs), Recurrent Neural Networks (RNNs), Variational Autoencoders (VAEs), and Wasserstein Generative Adversarial Networks (WGANs). After defining four types of PQAs scenarios, we focus on what we refer to as potential PQA, aiming to compare quantum models with the best-known classical algorithms for the task at hand. We let the models race on a well-defined and application-relevant competition setting, where we illustrate and demonstrate our framework on 20 variables (qubits) generative modeling task. Our results suggest that QCBMs are more efficient in the data-limited regime than the other state-of-the-art classical generative models. Such a feature is highly desirable in a wide range of real-world applications where the available data is scarce.

Do Quantum Circuit Born Machines Generalize?

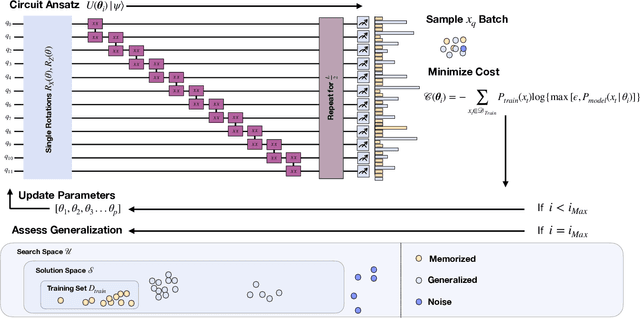
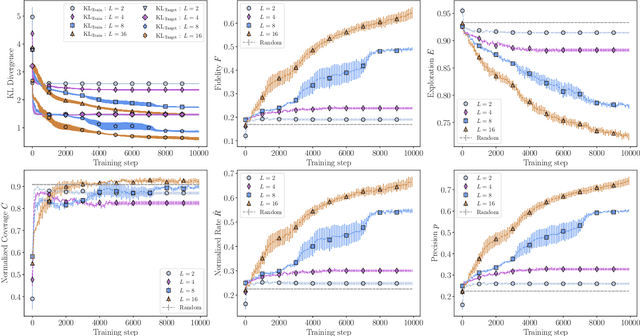
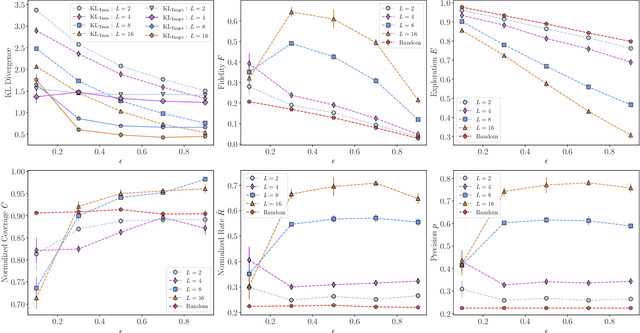
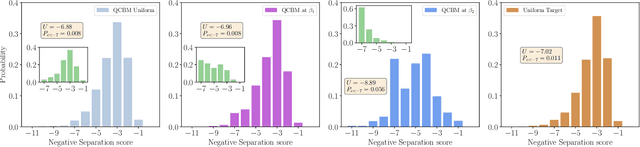
In recent proposals of quantum circuit models for generative tasks, the discussion about their performance has been limited to their ability to reproduce a known target distribution. For example, expressive model families such as Quantum Circuit Born Machines (QCBMs) have been almost entirely evaluated on their capability to learn a given target distribution with high accuracy. While this aspect may be ideal for some tasks, it limits the scope of a generative model's assessment to its ability to memorize data rather than generalize. As a result, there has been little understanding of a model's generalization performance and the relation between such capability and the resource requirements, e.g., the circuit depth and the amount of training data. In this work, we leverage upon a recently proposed generalization evaluation framework to begin addressing this knowledge gap. We first investigate the QCBM's learning process of a cardinality-constrained distribution and see an increase in generalization performance while increasing the circuit depth. In the 12-qubit example presented here, we observe that with as few as 30% of the valid patterns as the training set, the QCBM exhibits the best generalization performance toward generating unseen and valid patterns. Lastly, we assess the QCBM's ability to generalize not only to valid features, but to high-quality bitstrings distributed according to an adequately biased distribution. We see that the QCBM is able to effectively learn the bias and generate unseen samples with higher quality than those in the training set. To the best of our knowledge, this is the first work in the literature that presents the QCBM's generalization performance as an integral evaluation metric for quantum generative models, and demonstrates the QCBM's ability to generalize to high-quality, desired novel samples.

Evaluating Generalization in Classical and Quantum Generative Models

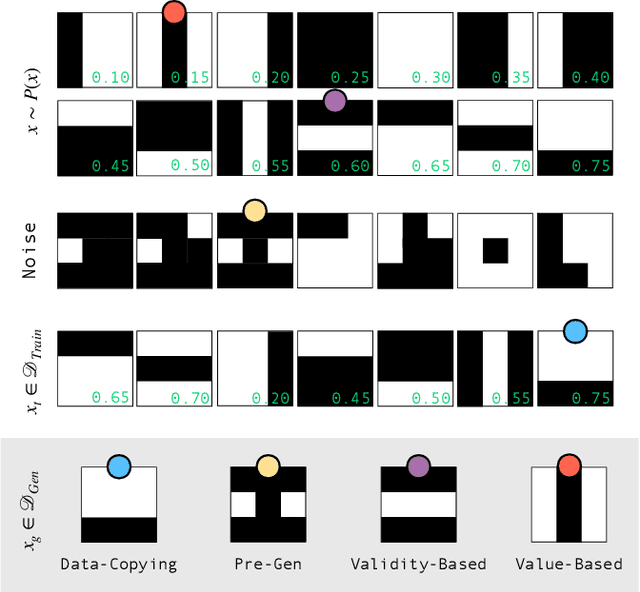
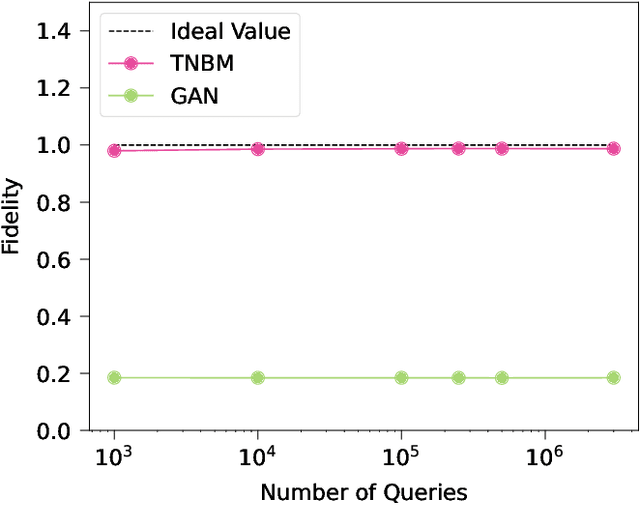
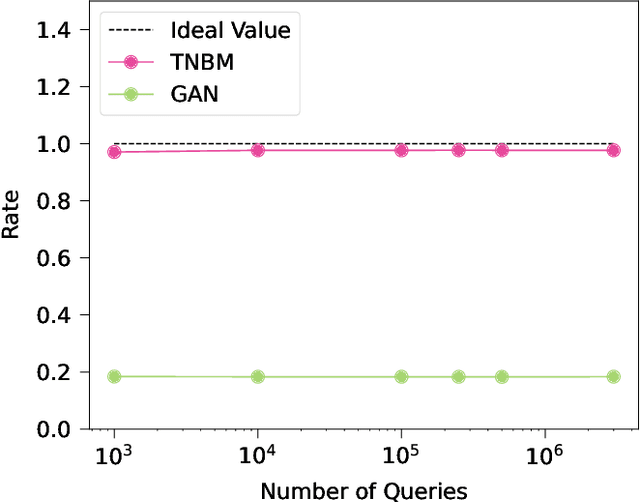
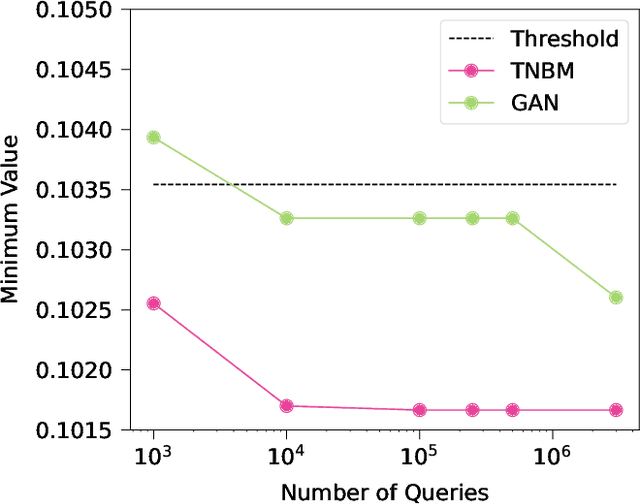
Defining and accurately measuring generalization in generative models remains an ongoing challenge and a topic of active research within the machine learning community. This is in contrast to discriminative models, where there is a clear definition of generalization, i.e., the model's classification accuracy when faced with unseen data. In this work, we construct a simple and unambiguous approach to evaluate the generalization capabilities of generative models. Using the sample-based generalization metrics proposed here, any generative model, from state-of-the-art classical generative models such as GANs to quantum models such as Quantum Circuit Born Machines, can be evaluated on the same ground on a concrete well-defined framework. In contrast to other sample-based metrics for probing generalization, we leverage constrained optimization problems (e.g., cardinality constrained problems) and use these discrete datasets to define specific metrics capable of unambiguously measuring the quality of the samples and the model's generalization capabilities for generating data beyond the training set but still within the valid solution space. Additionally, our metrics can diagnose trainability issues such as mode collapse and overfitting, as we illustrate when comparing GANs to quantum-inspired models built out of tensor networks. Our simulation results show that our quantum-inspired models have up to a $68 \times$ enhancement in generating unseen unique and valid samples compared to GANs, and a ratio of 61:2 for generating samples with better quality than those observed in the training set. We foresee these metrics as valuable tools for rigorously defining practical quantum advantage in the domain of generative modeling.

Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models

Mainstream machine-learning techniques such as deep learning and probabilistic programming rely heavily on sampling from generally intractable probability distributions. There is increasing interest in the potential advantages of using quantum computing technologies as sampling engines to speed up these tasks or to make them more effective. However, some pressing challenges in state-of-the-art quantum annealers have to be overcome before we can assess their actual performance. The sparse connectivity, resulting from the local interaction between quantum bits in physical hardware implementations, is considered the most severe limitation to the quality of constructing powerful generative unsupervised machine-learning models. Here we use embedding techniques to add redundancy to data sets, allowing us to increase the modeling capacity of quantum annealers. We illustrate our findings by training hardware-embedded graphical models on a binarized data set of handwritten digits and two synthetic data sets in experiments with up to 940 quantum bits. Our model can be trained in quantum hardware without full knowledge of the effective parameters specifying the corresponding quantum Gibbs-like distribution; therefore, this approach avoids the need to infer the effective temperature at each iteration, speeding up learning; it also mitigates the effect of noise in the control parameters, making it robust to deviations from the reference Gibbs distribution. Our approach demonstrates the feasibility of using quantum annealers for implementing generative models, and it provides a suitable framework for benchmarking these quantum technologies on machine-learning-related tasks.

Bayesian Network Structure Learning Using Quantum Annealing

We introduce a method for the problem of learning the structure of a Bayesian network using the quantum adiabatic algorithm. We do so by introducing an efficient reformulation of a standard posterior-probability scoring function on graphs as a pseudo-Boolean function, which is equivalent to a system of 2-body Ising spins, as well as suitable penalty terms for enforcing the constraints necessary for the reformulation; our proposed method requires $\mathcal O(n^2)$ qubits for $n$ Bayesian network variables. Furthermore, we prove lower bounds on the necessary weighting of these penalty terms. The logical structure resulting from the mapping has the appealing property that it is instance-independent for a given number of Bayesian network variables, as well as being independent of the number of data cases.