Do Quantum Circuit Born Machines Generalize?
Paper and Code
Jul 27, 2022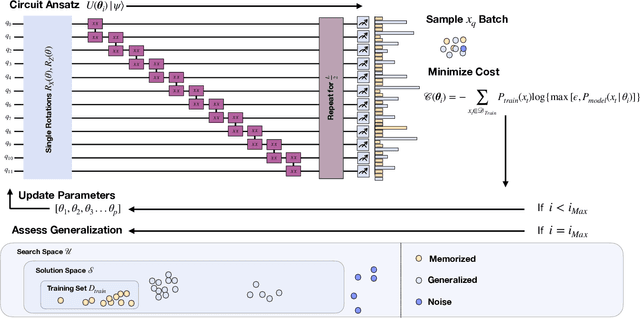
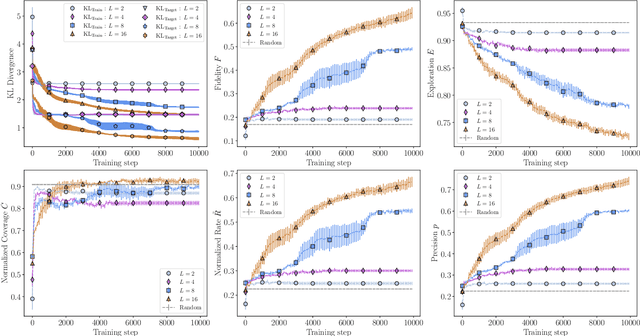
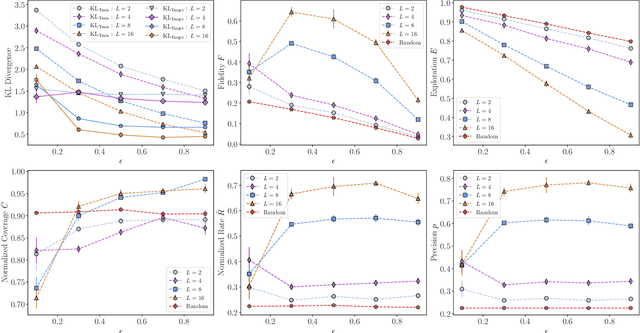
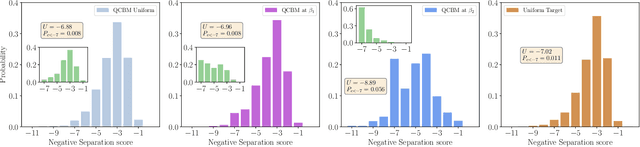
In recent proposals of quantum circuit models for generative tasks, the discussion about their performance has been limited to their ability to reproduce a known target distribution. For example, expressive model families such as Quantum Circuit Born Machines (QCBMs) have been almost entirely evaluated on their capability to learn a given target distribution with high accuracy. While this aspect may be ideal for some tasks, it limits the scope of a generative model's assessment to its ability to memorize data rather than generalize. As a result, there has been little understanding of a model's generalization performance and the relation between such capability and the resource requirements, e.g., the circuit depth and the amount of training data. In this work, we leverage upon a recently proposed generalization evaluation framework to begin addressing this knowledge gap. We first investigate the QCBM's learning process of a cardinality-constrained distribution and see an increase in generalization performance while increasing the circuit depth. In the 12-qubit example presented here, we observe that with as few as 30% of the valid patterns as the training set, the QCBM exhibits the best generalization performance toward generating unseen and valid patterns. Lastly, we assess the QCBM's ability to generalize not only to valid features, but to high-quality bitstrings distributed according to an adequately biased distribution. We see that the QCBM is able to effectively learn the bias and generate unseen samples with higher quality than those in the training set. To the best of our knowledge, this is the first work in the literature that presents the QCBM's generalization performance as an integral evaluation metric for quantum generative models, and demonstrates the QCBM's ability to generalize to high-quality, desired novel samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge