Do Quantum Circuit Born Machines Generalize?

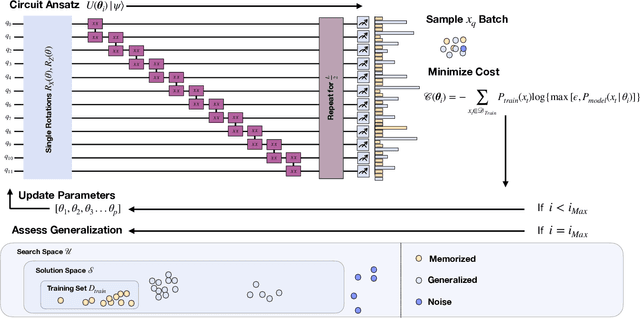
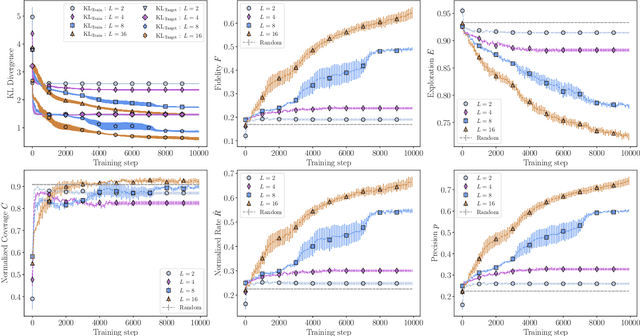
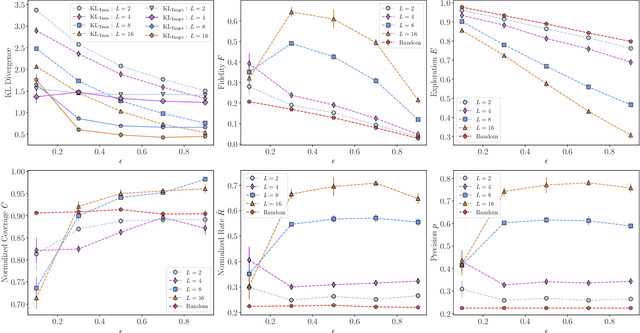
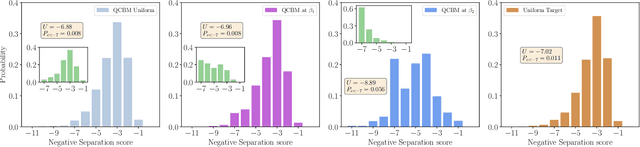
In recent proposals of quantum circuit models for generative tasks, the discussion about their performance has been limited to their ability to reproduce a known target distribution. For example, expressive model families such as Quantum Circuit Born Machines (QCBMs) have been almost entirely evaluated on their capability to learn a given target distribution with high accuracy. While this aspect may be ideal for some tasks, it limits the scope of a generative model's assessment to its ability to memorize data rather than generalize. As a result, there has been little understanding of a model's generalization performance and the relation between such capability and the resource requirements, e.g., the circuit depth and the amount of training data. In this work, we leverage upon a recently proposed generalization evaluation framework to begin addressing this knowledge gap. We first investigate the QCBM's learning process of a cardinality-constrained distribution and see an increase in generalization performance while increasing the circuit depth. In the 12-qubit example presented here, we observe that with as few as 30% of the valid patterns as the training set, the QCBM exhibits the best generalization performance toward generating unseen and valid patterns. Lastly, we assess the QCBM's ability to generalize not only to valid features, but to high-quality bitstrings distributed according to an adequately biased distribution. We see that the QCBM is able to effectively learn the bias and generate unseen samples with higher quality than those in the training set. To the best of our knowledge, this is the first work in the literature that presents the QCBM's generalization performance as an integral evaluation metric for quantum generative models, and demonstrates the QCBM's ability to generalize to high-quality, desired novel samples.

Introducing Non-Linearity into Quantum Generative Models

The evolution of an isolated quantum system is linear, and hence quantum algorithms are reversible, including those that utilize quantum circuits as generative machine learning models. However, some of the most successful classical generative models, such as those based on neural networks, involve highly non-linear and thus non-reversible dynamics. In this paper, we explore the effect of these dynamics in quantum generative modeling by introducing a model that adds non-linear activations via a neural network structure onto the standard Born Machine framework - the Quantum Neuron Born Machine (QNBM). To achieve this, we utilize a previously introduced Quantum Neuron subroutine, which is a repeat-until-success circuit with mid-circuit measurements and classical control. After introducing the QNBM, we investigate how its performance depends on network size, by training a 3-layer QNBM with 4 output neurons and various input and hidden layer sizes. We then compare our non-linear QNBM to the linear Quantum Circuit Born Machine (QCBM). We allocate similar time and memory resources to each model, such that the only major difference is the qubit overhead required by the QNBM. With gradient-based training, we show that while both models can easily learn a trivial uniform probability distribution, on a more challenging class of distributions, the QNBM achieves an almost 3x smaller error rate than a QCBM with a similar number of tunable parameters. We therefore show that non-linearity is a useful resource in quantum generative models, and we put forth the QNBM as a new model with good generative performance and potential for quantum advantage.