Generative Learning of Continuous Data by Tensor Networks

Beyond their origin in modeling many-body quantum systems, tensor networks have emerged as a promising class of models for solving machine learning problems, notably in unsupervised generative learning. While possessing many desirable features arising from their quantum-inspired nature, tensor network generative models have previously been largely restricted to binary or categorical data, limiting their utility in real-world modeling problems. We overcome this by introducing a new family of tensor network generative models for continuous data, which are capable of learning from distributions containing continuous random variables. We develop our method in the setting of matrix product states, first deriving a universal expressivity theorem proving the ability of this model family to approximate any reasonably smooth probability density function with arbitrary precision. We then benchmark the performance of this model on several synthetic and real-world datasets, finding that the model learns and generalizes well on distributions of continuous and discrete variables. We develop methods for modeling different data domains, and introduce a trainable compression layer which is found to increase model performance given limited memory or computational resources. Overall, our methods give important theoretical and empirical evidence of the efficacy of quantum-inspired methods for the rapidly growing field of generative learning.

Simplified Kalman filter for online rating: one-fits-all approach

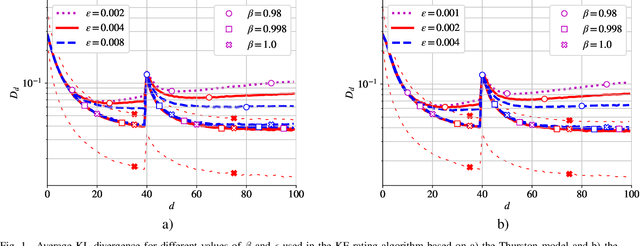
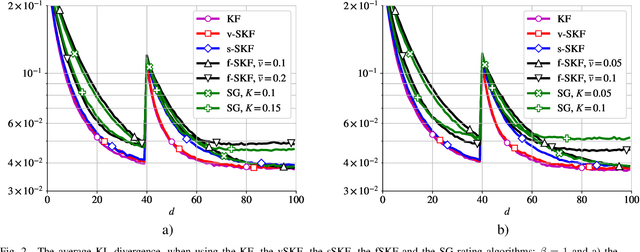
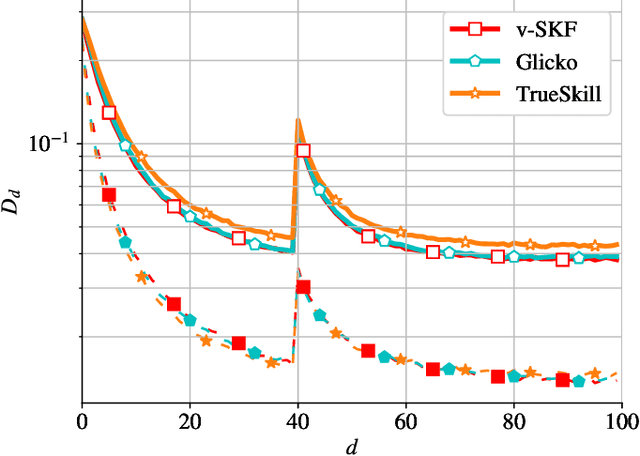
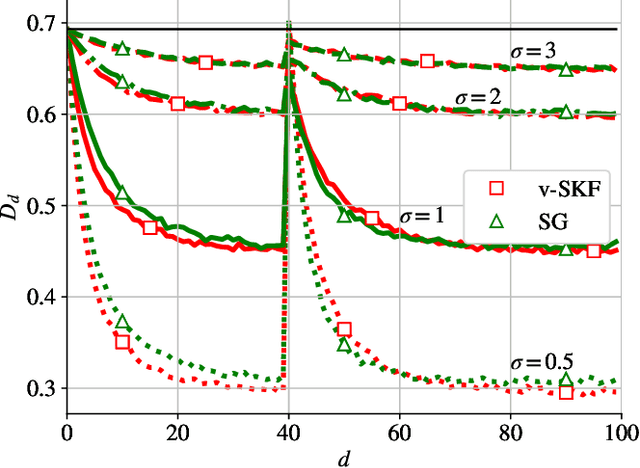
In this work, we deal with the problem of rating in sports, where the skills of the players/teams are inferred from the observed outcomes of the games. Our focus is on the online rating algorithms which estimate the skills after each new game by exploiting the probabilistic models of the relationship between the skills and the game outcome. We propose a Bayesian approach which may be seen as an approximate Kalman filter and which is generic in the sense that it can be used with any skills-outcome model and can be applied in the individual -- as well as in the group-sports. We show how the well-know algorithms (such as the Elo, the Glicko, and the TrueSkill algorithms) may be seen as instances of the one-fits-all approach we propose. In order to clarify the conditions under which the gains of the Bayesian approach over the simpler solutions can actually materialize, we critically compare the known and the new algorithms by means of numerical examples using the synthetic as well as the empirical data.