FIVB ranking: Misstep in the right direction

This work uses a statistical framework to present and evaluate the ranking algorithm that has been used by F\'ed\'eration Internationale de Volleyball (FIVB) since 2020. The salient feature of the FIVB ranking is the use of the probabilistic model, which explicitly calculates the probabilities of the games to come. This explicit modeling is new in the context of official ranking, and we study the optimality of its parameters as well as its relationship with the ranking algorithm as such. The analysis is carried out using both analytical and numerical methods. We conclude that, from the modeling perspective, the use of the home-field advantage (HFA) would be beneficial and that the weighting of the game results is counterproductive. Regarding the algorithm itself, we explain the rationale beyond the approximations currently used and explain how to find new parameters which improve the performance. Finally, we propose a new model that drastically simplifies both the implementation and interpretation of the resulting algorithm.

Automatic Regularization for Linear MMSE Filters

In this work, we consider the problem of regularization in minimum mean-squared error (MMSE) linear filters. Exploiting the relationship with statistical machine learning methods, the regularization parameter is found from the observed signals in a simple and automatic manner. The proposed approach is illustrated through system identification examples, where the automatic regularization yields near-optimal results.

A comprehensive analysis of the Elo rating algorithm: Stochastic model, convergence characteristics, design guidelines, and experimental results

The Elo algorithm, due to its simplicity, is widely used for rating in sports competitions as well as in other applications where the rating/ranking is a useful tool for predicting future results. However, despite its widespread use, a detailed understanding of the convergence properties of the Elo algorithm is still lacking. Aiming to fill this gap, this paper presents a comprehensive (stochastic) analysis of the Elo algorithm, considering round-robin (one-on-one) competitions. Specifically, analytical expressions are derived characterizing the behavior/evolution of the skills and of important performance metrics. Then, taking into account the relationship between the behavior of the algorithm and the step-size value, which is a hyperparameter that can be controlled, some design guidelines as well as discussions about the performance of the algorithm are provided. To illustrate the applicability of the theoretical findings, experimental results are shown, corroborating the very good match between analytical predictions and those obtained from the algorithm using real-world data (from the Italian SuperLega, Volleyball League).

Reliability of Solutions in Linear Ordering Problem: New Probabilistic Insight and Algorithms

In this work, our goal is to characterize the reliability of the solutions that can be obtained by the linear ordering problem (LOP) which is used to order $M$ objects from their pairwise comparisons. We adopt a probabilistic perspective, where the results of pairwise comparisons are modeled as Bernoulli variables with a common parameter which we estimate from the observed data. Estimation by brute-force enumeration has a prohibitive complexity of O($M!$) we thus reformulate the problem and introduce a concept of Slater's spectrum which generalizes Slater's index, and next, devising an efficient algorithm to find the spectrum, we lower the complexity to O($M^2 2^M$) which is manageable for moderate-size LOPs. Furthermore, with a minor modification of the algorithm, we are able to find all solutions of the LOP. Numerical examples on synthetic and real-world data are shown and the Python-implemented algorithms are publicly available.

FIFA ranking: Evaluation and path forward

In this work we study the ranking algorithm used by F\'ed\'eration Internationale de Football Association (FIFA); we analyze the parameters it currently uses, show the formal probabilistic model from which it can be derived, and optimize the latter. In particular, analyzing the games since the introduction of the algorithm in 2018, we conclude that the game's "importance" (as defined by FIFA) used in the algorithm is counterproductive from the point of view of the predictive capability of the algorithm. We also postulate the algorithm to be rooted in the formal modelling principle, where the Davidson model proposed in 1970 seems to be an excellent candidate, preserving the form of the algorithm currently used. The results indicate that the predictive capability of the algorithm is notably improved by using the home-field advantage and the explicit model for the draws in the game. Moderate, but notable improvement may be attained by introducing the weighting of the results with the goal differential, which although not rooted in a formal modelling principle, is compatible with the current algorithm and can be tuned to the characteristics of the football competition.

Simplified Kalman filter for online rating: one-fits-all approach

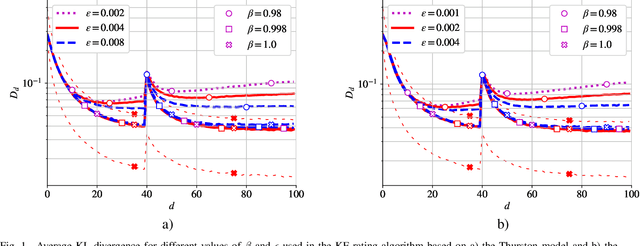
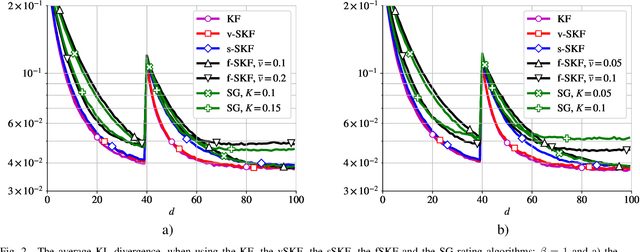
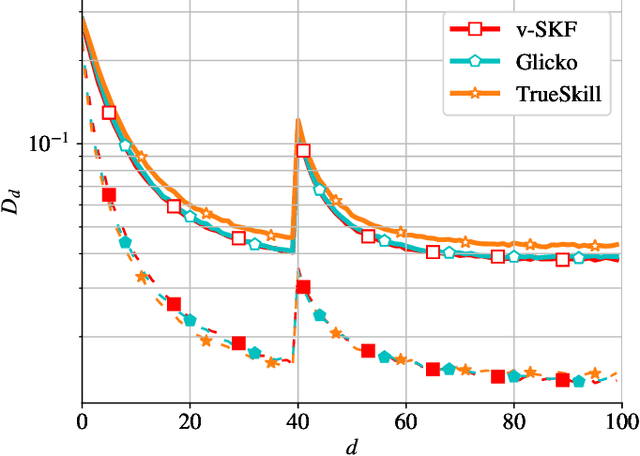
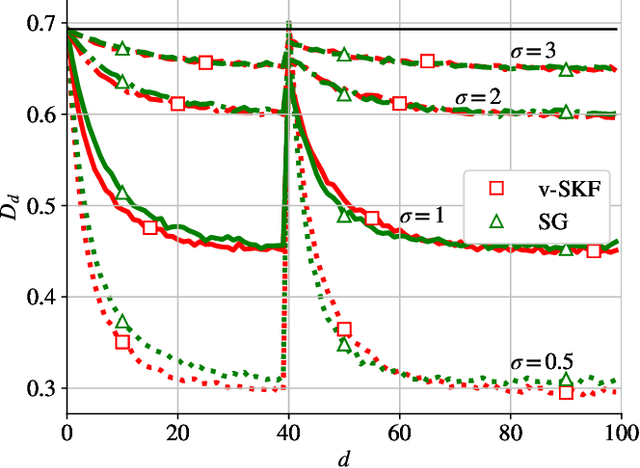
In this work, we deal with the problem of rating in sports, where the skills of the players/teams are inferred from the observed outcomes of the games. Our focus is on the online rating algorithms which estimate the skills after each new game by exploiting the probabilistic models of the relationship between the skills and the game outcome. We propose a Bayesian approach which may be seen as an approximate Kalman filter and which is generic in the sense that it can be used with any skills-outcome model and can be applied in the individual -- as well as in the group-sports. We show how the well-know algorithms (such as the Elo, the Glicko, and the TrueSkill algorithms) may be seen as instances of the one-fits-all approach we propose. In order to clarify the conditions under which the gains of the Bayesian approach over the simpler solutions can actually materialize, we critically compare the known and the new algorithms by means of numerical examples using the synthetic as well as the empirical data.

Elo-MOV rating algorithm: Generalization of the Elo algorithm by modelling the discretized Margin of Victory

In this work we develop a new algorithm for rating of teams (or players) in one-on-one games by exploiting the observed difference of the game-points (such as goals), also known as margin of victory (MOV). Our objective is to obtain the Elo-style algorithm whose operation is simple to implement and to understand intuitively. This is done in three steps: first, we define the probabilistic model between the teams' skills and the discretized margin of victory (MOV) variable. We thus use a predefined number of discretization categories, which generalizes the model underpinning the Elo algorithm, where the MOV variable is discretized to three categories (win/loss/draw). Second, with the formal probabilistic model at hand, the optimization required by the maximum likelihood (ML) rule is implemented via stochastic gradient (SG); this yields a simple on-line rating updates which are identical in general form to those of the Elo algorithm. The main difference lies in the way the scores and expected scores are defined. Third, we propose a simple method to estimate the coefficients of the model, and thus define the operation of the algorithm. This is done in closed form using the historical data so the algorithm is tailored to the sport of interest and the coefficients defining its operation are determined in entirely transparent manner. We show numerical examples based on the results of ten seasons of the English Premier Ligue (EPL).

Bilinear Models for Machine Learning

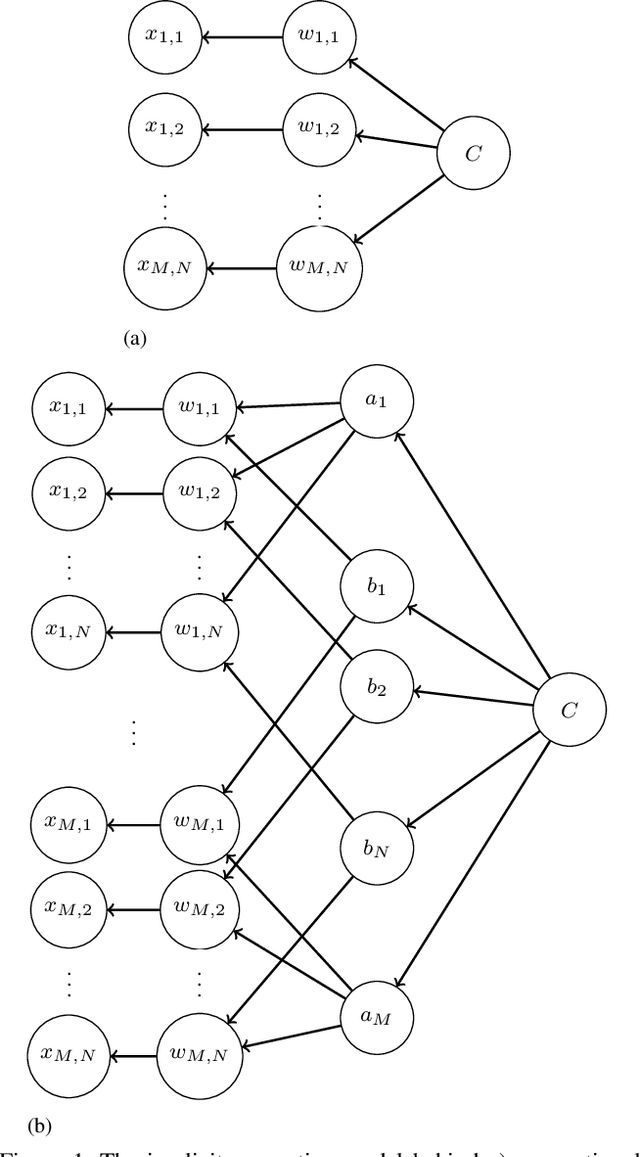
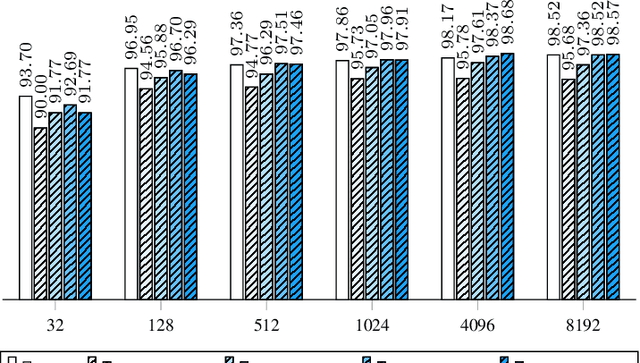
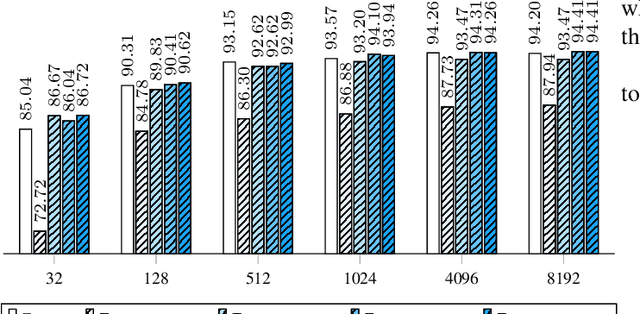
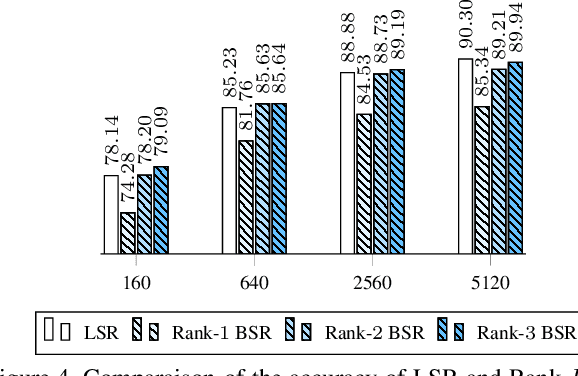
In this work we define and analyze the bilinear models which replace the conventional linear operation used in many building blocks of machine learning (ML). The main idea is to devise the ML algorithms which are adapted to the objects they treat. In the case of monochromatic images, we show that the bilinear operation exploits better the structure of the image than the conventional linear operation which ignores the spatial relationship between the pixels. This translates into significantly smaller number of parameters required to yield the same performance. We show numerical examples of classification in the MNIST data set.