Mutual Information-based Generalized Category Discovery

We introduce an information-maximization approach for the Generalized Category Discovery (GCD) problem. Specifically, we explore a parametric family of loss functions evaluating the mutual information between the features and the labels, and find automatically the one that maximizes the predictive performances. Furthermore, we introduce the Elbow Maximum Centroid-Shift (EMaCS) technique, which estimates the number of classes in the unlabeled set. We report comprehensive experiments, which show that our mutual information-based approach (MIB) is both versatile and highly competitive under various GCD scenarios. The gap between the proposed approach and the existing methods is significant, more so when dealing with fine-grained classification problems. Our code: \url{https://github.com/fchiaroni/Mutual-Information-Based-GCD}.

Simplex Clustering via sBeta with Applications to Online Adjustment of Black-Box Predictions

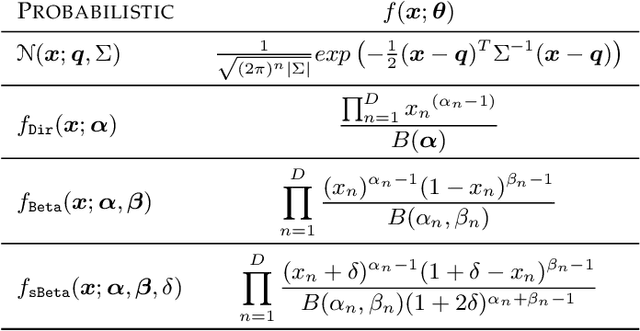
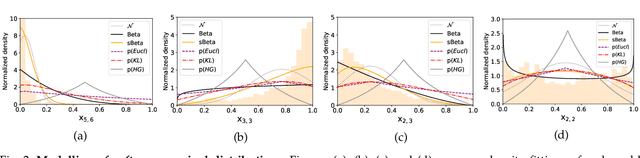
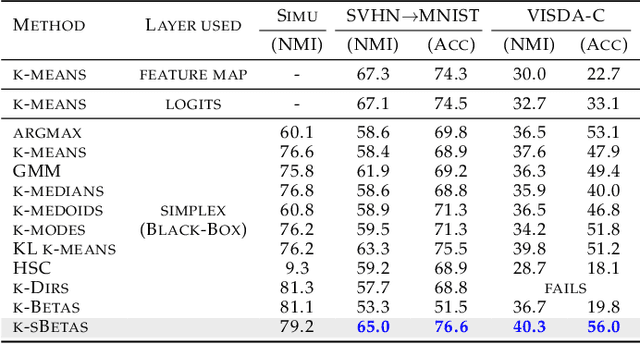
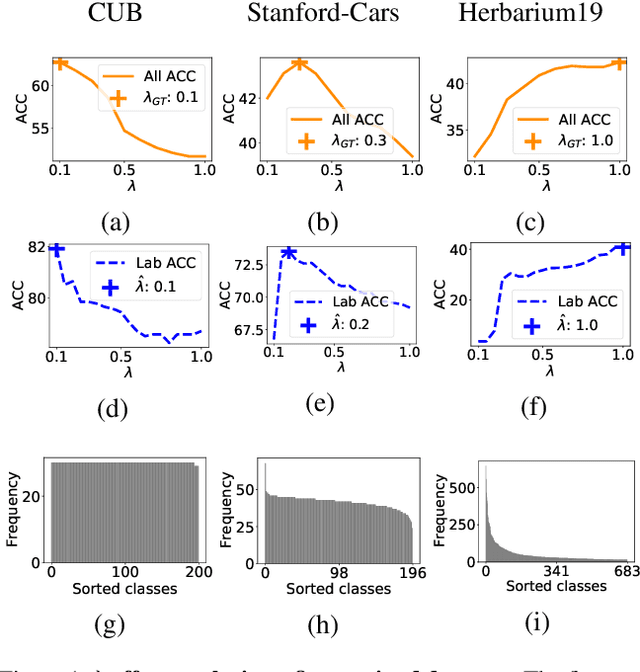
We explore clustering the softmax predictions of deep neural networks and introduce a novel probabilistic clustering method, referred to as k-sBetas. In the general context of clustering distributions, the existing methods focused on exploring distortion measures tailored to simplex data, such as the KL divergence, as alternatives to the standard Euclidean distance. We provide a general perspective of clustering distributions, which emphasizes that the statistical models underlying distortion-based methods may not be descriptive enough. Instead, we optimize a mixed-variable objective measuring the conformity of data within each cluster to the introduced sBeta density function, whose parameters are constrained and estimated jointly with binary assignment variables. Our versatile formulation approximates a variety of parametric densities for modeling cluster data, and enables to control the cluster-balance bias. This yields highly competitive performances for efficient unsupervised adjustment of black-box predictions in a variety of scenarios, including one-shot classification and unsupervised domain adaptation in real-time for road segmentation. Implementation is available at https://github.com/fchiaroni/Clustering_Softmax_Predictions.

Bilinear Models for Machine Learning

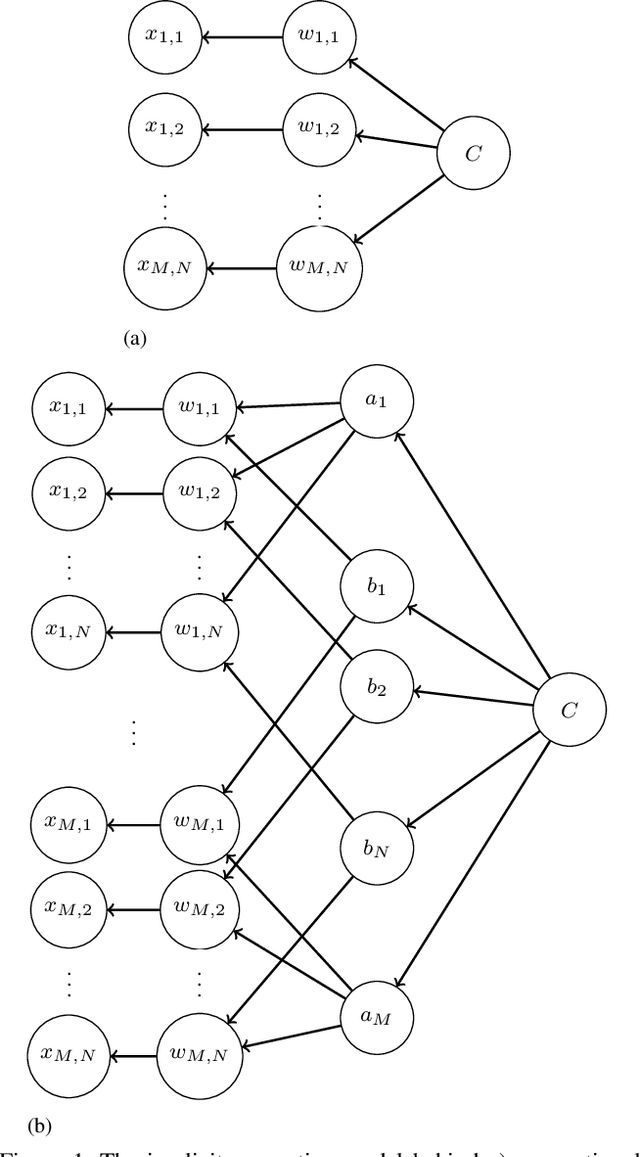
In this work we define and analyze the bilinear models which replace the conventional linear operation used in many building blocks of machine learning (ML). The main idea is to devise the ML algorithms which are adapted to the objects they treat. In the case of monochromatic images, we show that the bilinear operation exploits better the structure of the image than the conventional linear operation which ignores the spatial relationship between the pixels. This translates into significantly smaller number of parameters required to yield the same performance. We show numerical examples of classification in the MNIST data set.

Deep clustering: On the link between discriminative models and K-means

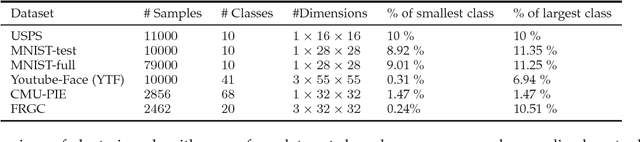
In the context of recent deep clustering studies, discriminative models dominate the literature and report the most competitive performances. These models learn a deep discriminative neural network classifier in which the labels are latent. Typically, they use multinomial logistic regression posteriors and parameter regularization, as is very common in supervised learning. It is generally acknowledged that discriminative objective functions (e.g., those based on the mutual information or the KL divergence) are more flexible than generative approaches (e.g., K-means) in the sense that they make fewer assumptions about the data distributions and, typically, yield much better unsupervised deep learning results. On the surface, several recent discriminative models may seem unrelated to K-means. This study shows that these models are, in fact, equivalent to K-means under mild conditions and common posterior models and parameter regularization. We prove that, for the commonly used logistic regression posteriors, maximizing the $L_2$ regularized mutual information via an approximate alternating direction method (ADM) is equivalent to a soft and regularized K-means loss. Our theoretical analysis not only connects directly several recent state-of-the-art discriminative models to K-means, but also leads to a new soft and regularized deep K-means algorithm, which yields competitive performance on several image clustering benchmarks.