Deep clustering: On the link between discriminative models and K-means
Paper and Code
Oct 09, 2018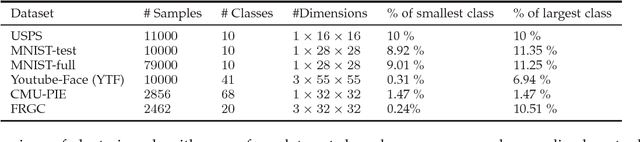

In the context of recent deep clustering studies, discriminative models dominate the literature and report the most competitive performances. These models learn a deep discriminative neural network classifier in which the labels are latent. Typically, they use multinomial logistic regression posteriors and parameter regularization, as is very common in supervised learning. It is generally acknowledged that discriminative objective functions (e.g., those based on the mutual information or the KL divergence) are more flexible than generative approaches (e.g., K-means) in the sense that they make fewer assumptions about the data distributions and, typically, yield much better unsupervised deep learning results. On the surface, several recent discriminative models may seem unrelated to K-means. This study shows that these models are, in fact, equivalent to K-means under mild conditions and common posterior models and parameter regularization. We prove that, for the commonly used logistic regression posteriors, maximizing the $L_2$ regularized mutual information via an approximate alternating direction method (ADM) is equivalent to a soft and regularized K-means loss. Our theoretical analysis not only connects directly several recent state-of-the-art discriminative models to K-means, but also leads to a new soft and regularized deep K-means algorithm, which yields competitive performance on several image clustering benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge