Simplified Kalman filter for online rating: one-fits-all approach
Paper and Code
Apr 28, 2021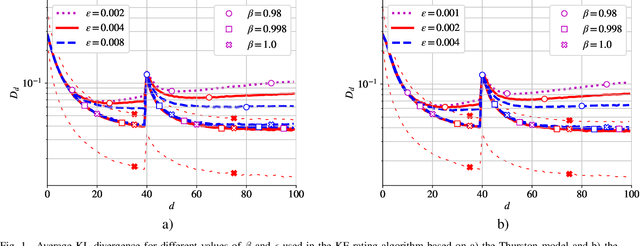
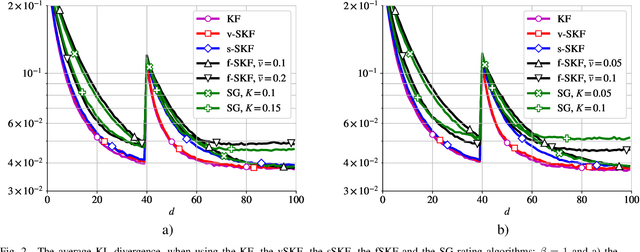
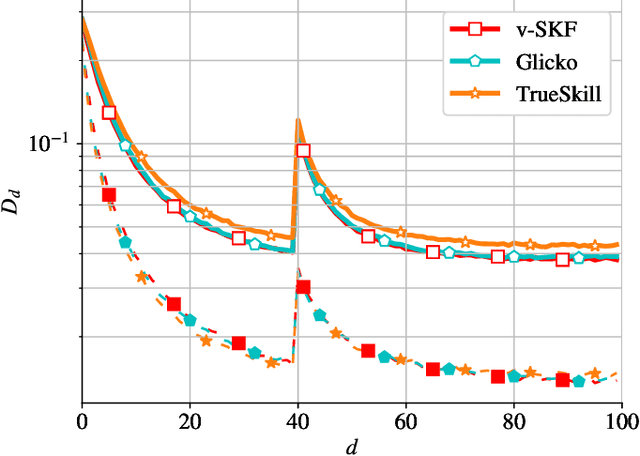
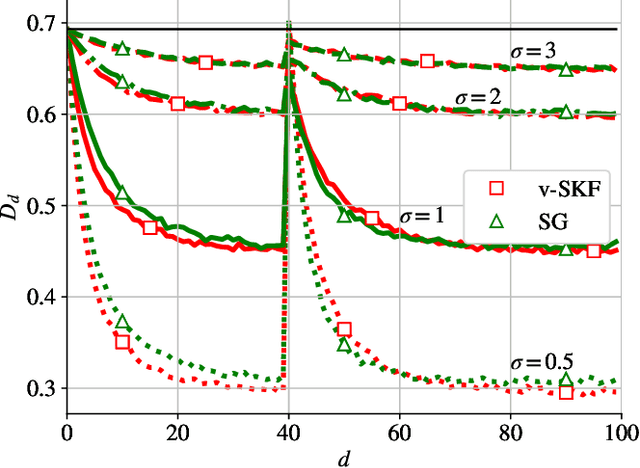
In this work, we deal with the problem of rating in sports, where the skills of the players/teams are inferred from the observed outcomes of the games. Our focus is on the online rating algorithms which estimate the skills after each new game by exploiting the probabilistic models of the relationship between the skills and the game outcome. We propose a Bayesian approach which may be seen as an approximate Kalman filter and which is generic in the sense that it can be used with any skills-outcome model and can be applied in the individual -- as well as in the group-sports. We show how the well-know algorithms (such as the Elo, the Glicko, and the TrueSkill algorithms) may be seen as instances of the one-fits-all approach we propose. In order to clarify the conditions under which the gains of the Bayesian approach over the simpler solutions can actually materialize, we critically compare the known and the new algorithms by means of numerical examples using the synthetic as well as the empirical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge