"Normalized Stress" is Not Normalized: How to Interpret Stress Correctly

Stress is among the most commonly employed quality metrics and optimization criteria for dimension reduction projections of high dimensional data. Complex, high dimensional data is ubiquitous across many scientific disciplines, including machine learning, biology, and the social sciences. One of the primary methods of visualizing these datasets is with two dimensional scatter plots that visually capture some properties of the data. Because visually determining the accuracy of these plots is challenging, researchers often use quality metrics to measure projection accuracy or faithfulness to the full data. One of the most commonly employed metrics, normalized stress, is sensitive to uniform scaling of the projection, despite this act not meaningfully changing anything about the projection. We investigate the effect of scaling on stress and other distance based quality metrics analytically and empirically by showing just how much the values change and how this affects dimension reduction technique evaluations. We introduce a simple technique to make normalized stress scale invariant and show that it accurately captures expected behavior on a small benchmark.

Generative Learning of Continuous Data by Tensor Networks

Beyond their origin in modeling many-body quantum systems, tensor networks have emerged as a promising class of models for solving machine learning problems, notably in unsupervised generative learning. While possessing many desirable features arising from their quantum-inspired nature, tensor network generative models have previously been largely restricted to binary or categorical data, limiting their utility in real-world modeling problems. We overcome this by introducing a new family of tensor network generative models for continuous data, which are capable of learning from distributions containing continuous random variables. We develop our method in the setting of matrix product states, first deriving a universal expressivity theorem proving the ability of this model family to approximate any reasonably smooth probability density function with arbitrary precision. We then benchmark the performance of this model on several synthetic and real-world datasets, finding that the model learns and generalizes well on distributions of continuous and discrete variables. We develop methods for modeling different data domains, and introduce a trainable compression layer which is found to increase model performance given limited memory or computational resources. Overall, our methods give important theoretical and empirical evidence of the efficacy of quantum-inspired methods for the rapidly growing field of generative learning.

Balancing between the Local and Global Structures (LGS) in Graph Embedding

We present a method for balancing between the Local and Global Structures (LGS) in graph embedding, via a tunable parameter. Some embedding methods aim to capture global structures, while others attempt to preserve local neighborhoods. Few methods attempt to do both, and it is not always possible to capture well both local and global information in two dimensions, which is where most graph drawing live. The choice of using a local or a global embedding for visualization depends not only on the task but also on the structure of the underlying data, which may not be known in advance. For a given graph, LGS aims to find a good balance between the local and global structure to preserve. We evaluate the performance of LGS with synthetic and real-world datasets and our results indicate that it is competitive with the state-of-the-art methods, using established quality metrics such as stress and neighborhood preservation. We introduce a novel quality metric, cluster distance preservation, to assess intermediate structure capture. All source-code, datasets, experiments and analysis are available online.

Probabilistic Graphical Models and Tensor Networks: A Hybrid Framework

We investigate a correspondence between two formalisms for discrete probabilistic modeling: probabilistic graphical models (PGMs) and tensor networks (TNs), a powerful modeling framework for simulating complex quantum systems. The graphical calculus of PGMs and TNs exhibits many similarities, with discrete undirected graphical models (UGMs) being a special case of TNs. However, more general probabilistic TN models such as Born machines (BMs) employ complex-valued hidden states to produce novel forms of correlation among the probabilities. While representing a new modeling resource for capturing structure in discrete probability distributions, this behavior also renders the direct application of standard PGM tools impossible. We aim to bridge this gap by introducing a hybrid PGM-TN formalism that integrates quantum-like correlations into PGM models in a principled manner, using the physically-motivated concept of decoherence. We first prove that applying decoherence to the entirety of a BM model converts it into a discrete UGM, and conversely, that any subgraph of a discrete UGM can be represented as a decohered BM. This method allows a broad family of probabilistic TN models to be encoded as partially decohered BMs, a fact we leverage to combine the representational strengths of both model families. We experimentally verify the performance of such hybrid models in a sequential modeling task, and identify promising uses of our method within the context of existing applications of graphical models.

Adaptive Epidemic Forecasting and Community Risk Evaluation of COVID-19

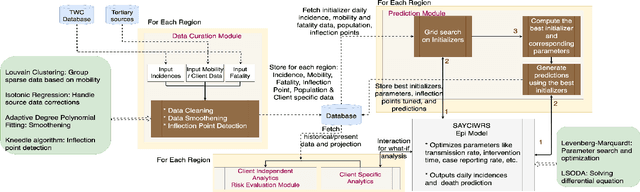
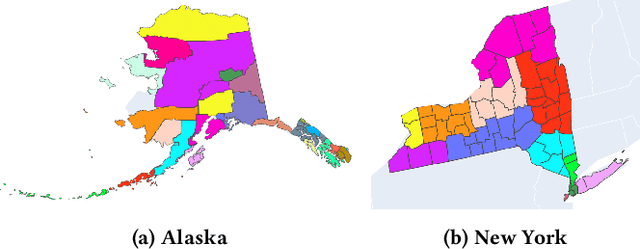
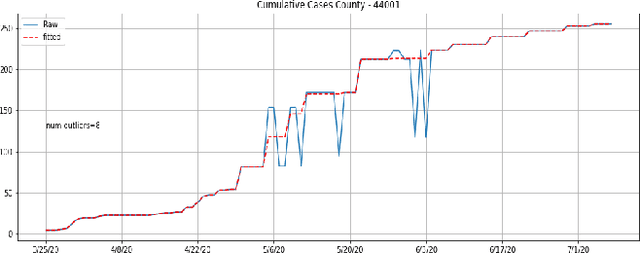
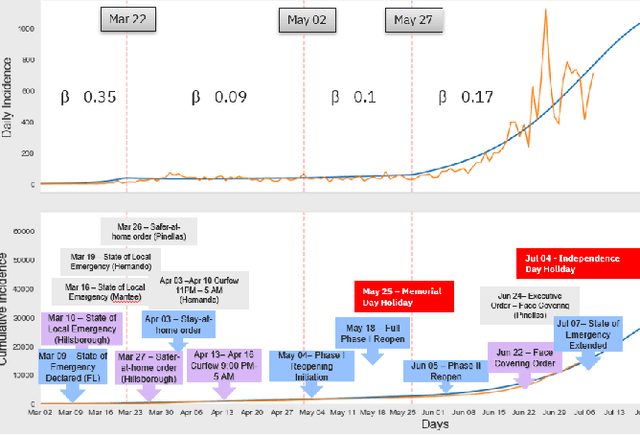
Pandemic control measures like lock-down, restrictions on restaurants and gatherings, social-distancing have shown to be effective in curtailing the spread of COVID-19. However, their sustained enforcement has negative economic effects. To craft strategies and policies that reduce the hardship on the people and the economy while being effective against the pandemic, authorities need to understand the disease dynamics at the right geo-spatial granularity. Considering factors like the hospitals' ability to handle the fluctuating demands, evaluating various reopening scenarios, and accurate forecasting of cases are vital to decision making. Towards this end, we present a flexible end-to-end solution that seamlessly integrates public health data with tertiary client data to accurately estimate the risk of reopening a community. At its core lies a state-of-the-art prediction model that auto-captures changing trends in transmission and mobility. Benchmarking against various published baselines confirm the superiority of our forecasting algorithm. Combined with the ability to extend to multiple client-specific requirements and perform deductive reasoning through counter-factual analysis, this solution provides actionable insights to multiple client domains ranging from government to educational institutions, hospitals, and commercial establishments.

Quantum Tensor Networks, Stochastic Processes, and Weighted Automata

Modeling joint probability distributions over sequences has been studied from many perspectives. The physics community developed matrix product states, a tensor-train decomposition for probabilistic modeling, motivated by the need to tractably model many-body systems. But similar models have also been studied in the stochastic processes and weighted automata literature, with little work on how these bodies of work relate to each other. We address this gap by showing how stationary or uniform versions of popular quantum tensor network models have equivalent representations in the stochastic processes and weighted automata literature, in the limit of infinitely long sequences. We demonstrate several equivalence results between models used in these three communities: (i) uniform variants of matrix product states, Born machines and locally purified states from the quantum tensor networks literature, (ii) predictive state representations, hidden Markov models, norm-observable operator models and hidden quantum Markov models from the stochastic process literature,and (iii) stochastic weighted automata, probabilistic automata and quadratic automata from the formal languages literature. Such connections may open the door for results and methods developed in one area to be applied in another.

Adaptive Tensor Learning with Tensor Networks

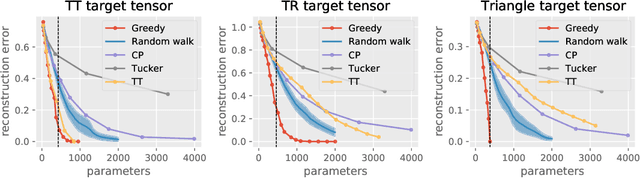
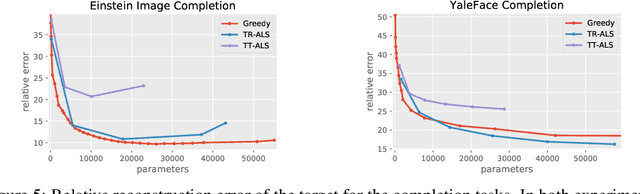
Tensor decomposition techniques have shown great successes in machine learning and data science by extending classical algorithms based on matrix factorization to multi-modal and multi-way data. However, there exist many tensor decomposition models~(CP, Tucker, Tensor Train, etc.) and the rank of such a decomposition is typically a collection of integers rather than a unique number, making model and hyper-parameter selection a tedious and costly task. At the same time, tensor network methods are powerful tools developed in the physics community which have recently shown their potential for machine learning applications and offer a unifying view of the various tensor decomposition models. In this paper, we leverage the tensor network formalism to develop a generic and efficient adaptive algorithm for tensor learning. Our method is based on a simple greedy approach optimizing a differentiable loss function starting from a rank one tensor and successively identifying the most promising tensor network edges for small rank increments. Our algorithm can adaptively identify tensor network structures with small number of parameters that effectively optimize the objective function from data. The framework we introduce is very broad and encompasses many common tensor optimization problems. Experiments on tensor decomposition and tensor completion tasks with both synthetic and real world data demonstrate the effectiveness of the proposed algorithm.

Tensor Networks for Language Modeling

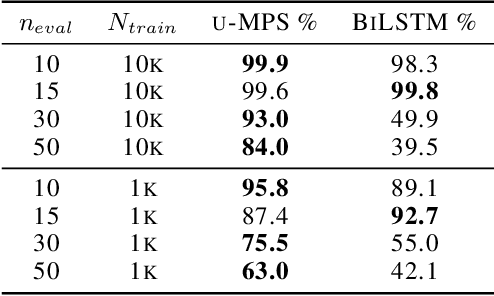
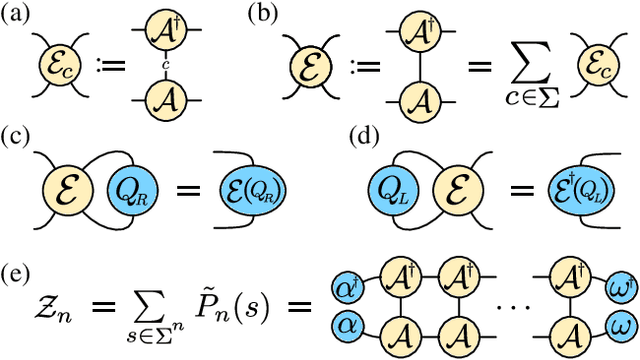
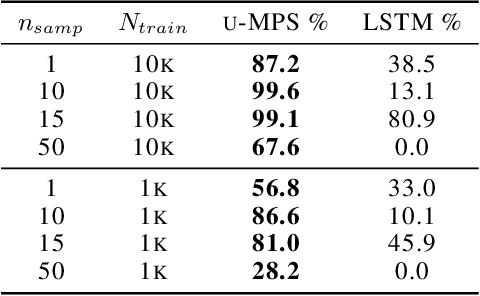
The tensor network formalism has enjoyed over two decades of success in modeling the behavior of complex quantum-mechanical systems, but has only recently and sporadically been leveraged in machine learning. Here we introduce a uniform matrix product state (u-MPS) model for probabilistic modeling of sequence data. We identify several distinctive features of this recurrent generative model, notably the ability to condition or marginalize sampling on characters at arbitrary locations within a sequence, with no need for approximate sampling methods. Despite the sequential architecture of u-MPS, we show that a recursive evaluation algorithm can be used to parallelize its inference and training, with a string of length n only requiring parallel time $\mathcal{O}(\log n)$ to evaluate. Experiments on a context-free language demonstrate a strong capacity to learn grammatical structure from limited data, pointing towards the potential of tensor networks for language modeling applications.