Stephen Kobourov
Visualization Tasks for Unlabelled Graphs
Apr 19, 2025Abstract:We investigate tasks that can be accomplished with unlabelled graphs, where nodes do not have persistent or semantically meaningful labels. New techniques to visualize these graphs have been proposed, but more understanding of unlabelled graph tasks is required before they can be adequately evaluated. Some tasks apply to both labelled and unlabelled graphs, but many do not translate between these contexts. We propose a taxonomy of unlabelled graph abstract tasks, organized according to the Scope of the data at play, the Action intended by the user, and the Target data under consideration. We show the descriptive power of this task abstraction by connecting to concrete examples from previous frameworks, and connect these abstractions to real-world problems. To showcase the evaluative power of the taxonomy, we perform a preliminary assessment of 6 visualizations for each task. For each combination of task and visual encoding, we consider the effort required from viewers, the likelihood of task success, and how both factors vary between small-scale and large-scale graphs.
"Normalized Stress" is Not Normalized: How to Interpret Stress Correctly
Aug 14, 2024Abstract:Stress is among the most commonly employed quality metrics and optimization criteria for dimension reduction projections of high dimensional data. Complex, high dimensional data is ubiquitous across many scientific disciplines, including machine learning, biology, and the social sciences. One of the primary methods of visualizing these datasets is with two dimensional scatter plots that visually capture some properties of the data. Because visually determining the accuracy of these plots is challenging, researchers often use quality metrics to measure projection accuracy or faithfulness to the full data. One of the most commonly employed metrics, normalized stress, is sensitive to uniform scaling of the projection, despite this act not meaningfully changing anything about the projection. We investigate the effect of scaling on stress and other distance based quality metrics analytically and empirically by showing just how much the values change and how this affects dimension reduction technique evaluations. We introduce a simple technique to make normalized stress scale invariant and show that it accurately captures expected behavior on a small benchmark.
Graph Sparsifications using Neural Network Assisted Monte Carlo Tree Search
Nov 17, 2023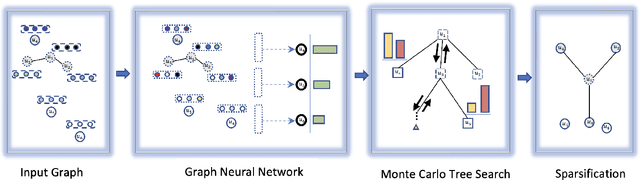

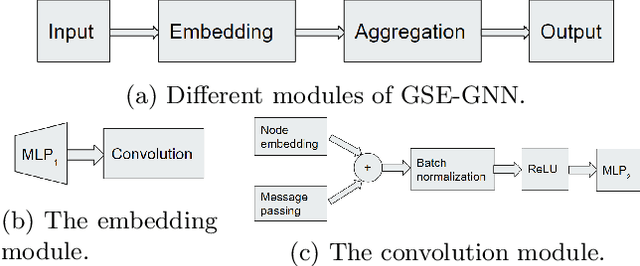
Abstract:Graph neural networks have been successful for machine learning, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing graph sparsifiers by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a sparsifier. The proposed method consistently outperforms several standard approximation algorithms on different types of graphs and often finds the optimal solution.
Balancing between the Local and Global Structures (LGS) in Graph Embedding
Sep 02, 2023Abstract:We present a method for balancing between the Local and Global Structures (LGS) in graph embedding, via a tunable parameter. Some embedding methods aim to capture global structures, while others attempt to preserve local neighborhoods. Few methods attempt to do both, and it is not always possible to capture well both local and global information in two dimensions, which is where most graph drawing live. The choice of using a local or a global embedding for visualization depends not only on the task but also on the structure of the underlying data, which may not be known in advance. For a given graph, LGS aims to find a good balance between the local and global structure to preserve. We evaluate the performance of LGS with synthetic and real-world datasets and our results indicate that it is competitive with the state-of-the-art methods, using established quality metrics such as stress and neighborhood preservation. We introduce a novel quality metric, cluster distance preservation, to assess intermediate structure capture. All source-code, datasets, experiments and analysis are available online.
Nearly Optimal Steiner Trees using Graph Neural Network Assisted Monte Carlo Tree Search
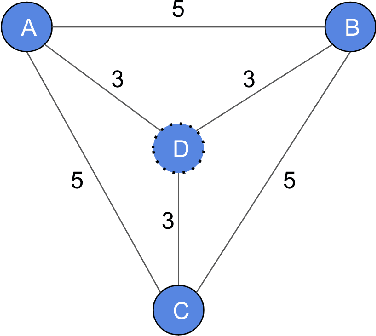
Apr 30, 2023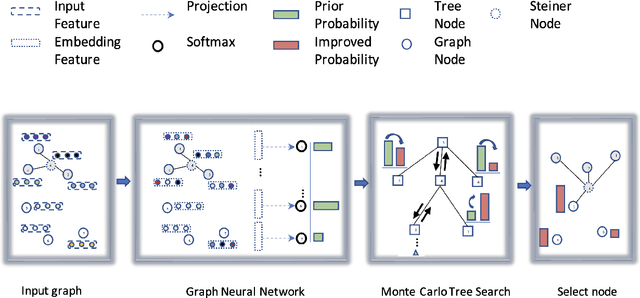



Abstract:Graph neural networks are useful for learning problems, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing Steiner Trees by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a Steiner tree. The proposed method consistently outperforms the standard 2-approximation algorithm on many different types of graphs and often finds the optimal solution.
Embedding Neighborhoods Simultaneously t-SNE (ENS-t-SNE)
May 24, 2022

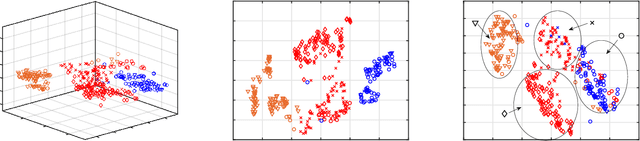
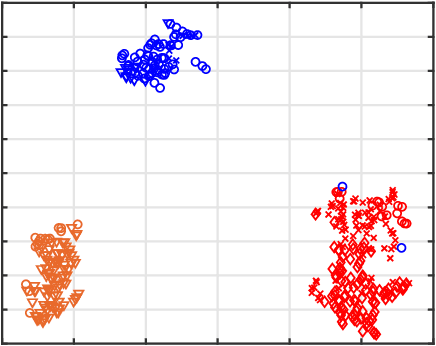
Abstract:We propose an algorithm for visualizing a dataset by embedding it in 3-dimensional Euclidean space based on various given distances between the same pairs of datapoints. Its aim is to find an Embedding which preserves Neighborhoods Simultaneously for all given distances by generalizing the t-Stochastic Neighborhood Embedding approach (ENS-t-SNE). We illustrate the utility of ENS-t-SNE by demonstrating its use in three applications. First, to visualize different notions of clusters and groups within the same high-dimensional dataset with one 3-dimensional embedding, as opposed to providing different embeddings of the same data and trying to match the corresponding points. Second, to illustrate the effects of different hyper-parameters of the classical t-SNE. Third, by considering multiple different notions of clustering in data, ENS-t-SNE can generate an alternative embedding than the classic t-SNE. We provide an extensive quantitative evaluation with real-world and synthetic datasets of different sizes and using different numbers of projections.
Computing Steiner Trees using Graph Neural Networks
Aug 18, 2021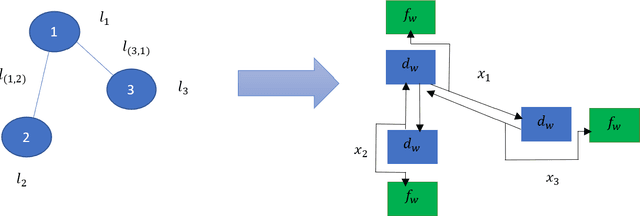
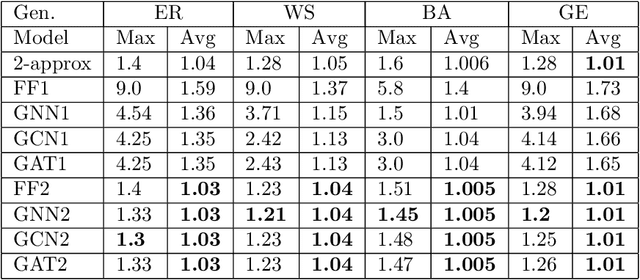
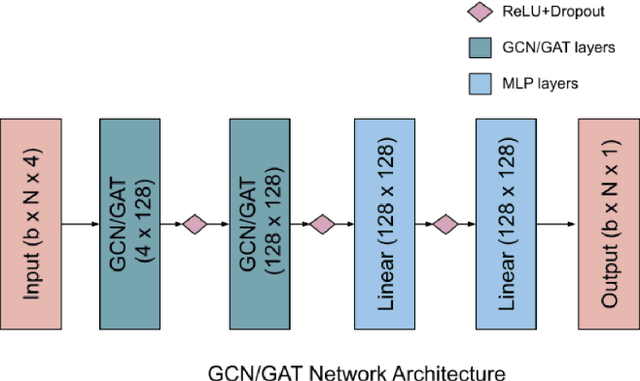
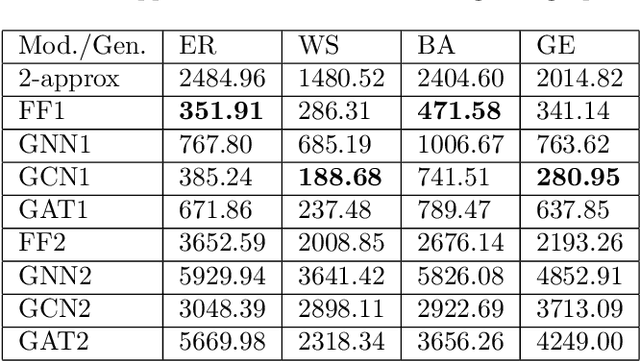
Abstract:Graph neural networks have been successful in many learning problems and real-world applications. A recent line of research explores the power of graph neural networks to solve combinatorial and graph algorithmic problems such as subgraph isomorphism, detecting cliques, and the traveling salesman problem. However, many NP-complete problems are as of yet unexplored using this method. In this paper, we tackle the Steiner Tree Problem. We employ four learning frameworks to compute low cost Steiner trees: feed-forward neural networks, graph neural networks, graph convolutional networks, and a graph attention model. We use these frameworks in two fundamentally different ways: 1) to train the models to learn the actual Steiner tree nodes, 2) to train the model to learn good Steiner point candidates to be connected to the constructed tree using a shortest path in a greedy fashion. We illustrate the robustness of our heuristics on several random graph generation models as well as the SteinLib data library. Our finding suggests that the out-of-the-box application of GNN methods does worse than the classic 2-approximation method. However, when combined with a greedy shortest path construction, it even does slightly better than the 2-approximation algorithm. This result sheds light on the fundamental capabilities and limitations of graph learning techniques on classical NP-complete problems.
The Language of Food during the Pandemic: Hints about the Dietary Effects of Covid-19
Oct 15, 2020



Abstract:We study the language of food on Twitter during the pandemic lockdown in the United States, focusing on the two month period of March 15 to May 15, 2020. Specifically, we analyze over770,000 tweets published during the lockdown and the equivalent period in the five previous years and highlight several worrying trends. First, we observe that during the lockdown there was a notable shift from mentions of healthy foods to unhealthy foods. Second, we show an increased pointwise mutual information of depression hashtags with food-related tweets posted during the lockdown and an increased association between depression hashtags and unhealthy foods, tobacco, and alcohol during the lockdown.
Multi-Perspective, Simultaneous Embedding
Sep 13, 2019



Abstract:We describe a method for simultaneous visualization of multiple pairwise distances in 3 dimensional (3D) space. Given the distance matrices that correspond to 2 dimensional projections of a 3 dimensional object (dataset) the goal is to recover the 3 dimensional object (dataset). We propose an approach that uses 3D to place the points, along with projections (planes) that preserve each of the given distance matrices. Our multi-perspective, simultaneous embedding (MPSE) method is based on non-linear dimensionality reduction that generalizes multidimensional scaling. We consider two versions of the problem: in the first one we are given the input distance matrices and the projections (e.g., if we have 3 different projections we can use the three orthogonal directions of the unit cube). In the second version of the problem we also compute the best projections as part of the optimization. We experimentally evaluate MPSE using synthetic datasets that illustrate the quality of the resulting solutions. Finally, we provide a functional prototype which implements both settings.
Stress-Plus-X (SPX) Graph Layout
Aug 23, 2019



Abstract:Stress, edge crossings, and crossing angles play an important role in the quality and readability of graph drawings. Most standard graph drawing algorithms optimize one of these criteria which may lead to layouts that are deficient in other criteria. We introduce an optimization framework, Stress-Plus-X (SPX), that simultaneously optimizes stress together with several other criteria: edge crossings, minimum crossing angle, and upwardness (for directed acyclic graphs). SPX achieves results that are close to the state-of-the-art algorithms that optimize these metrics individually. SPX is flexible and extensible and can optimize a subset or all of these criteria simultaneously. Our experimental analysis shows that our joint optimization approach is successful in drawing graphs with good performance across readability criteria.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge