Overlapping Community Detection using Dynamic Dilated Aggregation in Deep Residual GCN

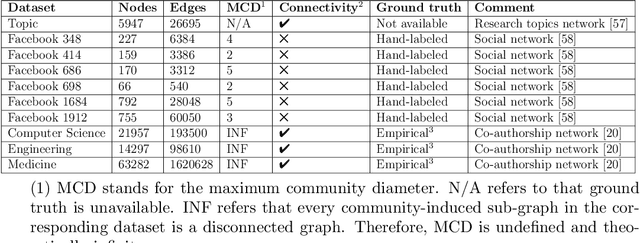
Overlapping community detection is a key problem in graph mining. Some research has considered applying graph convolutional networks (GCN) to tackle the problem. However, it is still challenging to incorporate deep graph convolutional networks in the case of general irregular graphs. In this study, we design a deep dynamic residual graph convolutional network (DynaResGCN) based on our novel dynamic dilated aggregation mechanisms and a unified end-to-end encoder-decoder-based framework to detect overlapping communities in networks. The deep DynaResGCN model is used as the encoder, whereas we incorporate the Bernoulli-Poisson (BP) model as the decoder. Consequently, we apply our overlapping community detection framework in a research topics dataset without having ground truth, a set of networks from Facebook having a reliable (hand-labeled) ground truth, and in a set of very large co-authorship networks having empirical (not hand-labeled) ground truth. Our experimentation on these datasets shows significantly superior performance over many state-of-the-art methods for the detection of overlapping communities in networks.

Embedding Neighborhoods Simultaneously t-SNE (ENS-t-SNE)

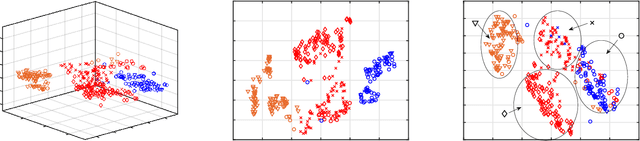
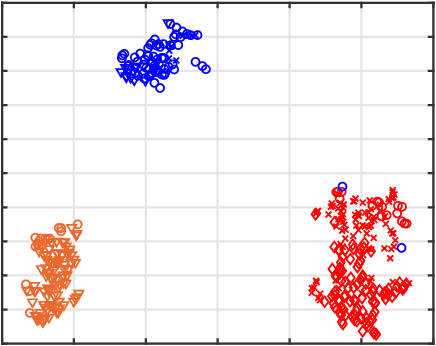
We propose an algorithm for visualizing a dataset by embedding it in 3-dimensional Euclidean space based on various given distances between the same pairs of datapoints. Its aim is to find an Embedding which preserves Neighborhoods Simultaneously for all given distances by generalizing the t-Stochastic Neighborhood Embedding approach (ENS-t-SNE). We illustrate the utility of ENS-t-SNE by demonstrating its use in three applications. First, to visualize different notions of clusters and groups within the same high-dimensional dataset with one 3-dimensional embedding, as opposed to providing different embeddings of the same data and trying to match the corresponding points. Second, to illustrate the effects of different hyper-parameters of the classical t-SNE. Third, by considering multiple different notions of clustering in data, ENS-t-SNE can generate an alternative embedding than the classic t-SNE. We provide an extensive quantitative evaluation with real-world and synthetic datasets of different sizes and using different numbers of projections.

Multi-Perspective, Simultaneous Embedding

We describe a method for simultaneous visualization of multiple pairwise distances in 3 dimensional (3D) space. Given the distance matrices that correspond to 2 dimensional projections of a 3 dimensional object (dataset) the goal is to recover the 3 dimensional object (dataset). We propose an approach that uses 3D to place the points, along with projections (planes) that preserve each of the given distance matrices. Our multi-perspective, simultaneous embedding (MPSE) method is based on non-linear dimensionality reduction that generalizes multidimensional scaling. We consider two versions of the problem: in the first one we are given the input distance matrices and the projections (e.g., if we have 3 different projections we can use the three orthogonal directions of the unit cube). In the second version of the problem we also compute the best projections as part of the optimization. We experimentally evaluate MPSE using synthetic datasets that illustrate the quality of the resulting solutions. Finally, we provide a functional prototype which implements both settings.

Symmetry Detection and Classification in Drawings of Graphs

Symmetry is a key feature observed in nature (from flowers and leaves, to butterflies and birds) and in human-made objects (from paintings and sculptures, to manufactured objects and architectural design). Rotational, translational, and especially reflectional symmetries, are also important in drawings of graphs. Detecting and classifying symmetries can be very useful in algorithms that aim to create symmetric graph drawings and in this paper we present a machine learning approach for these tasks. Specifically, we show that deep neural networks can be used to detect reflectional symmetries with 92% accuracy. We also build a multi-class classifier to distinguish between reflectional horizontal, reflectional vertical, rotational, and translational symmetries. Finally, we make available a collection of images of graph drawings with specific symmetric features that can be used in machine learning systems for training, testing and validation purposes. Our datasets, best trained ML models, source code are available online.