Embedding Neighborhoods Simultaneously t-SNE (ENS-t-SNE)

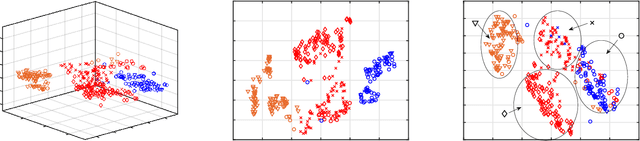
We propose an algorithm for visualizing a dataset by embedding it in 3-dimensional Euclidean space based on various given distances between the same pairs of datapoints. Its aim is to find an Embedding which preserves Neighborhoods Simultaneously for all given distances by generalizing the t-Stochastic Neighborhood Embedding approach (ENS-t-SNE). We illustrate the utility of ENS-t-SNE by demonstrating its use in three applications. First, to visualize different notions of clusters and groups within the same high-dimensional dataset with one 3-dimensional embedding, as opposed to providing different embeddings of the same data and trying to match the corresponding points. Second, to illustrate the effects of different hyper-parameters of the classical t-SNE. Third, by considering multiple different notions of clustering in data, ENS-t-SNE can generate an alternative embedding than the classic t-SNE. We provide an extensive quantitative evaluation with real-world and synthetic datasets of different sizes and using different numbers of projections.

Multi-Perspective, Simultaneous Embedding

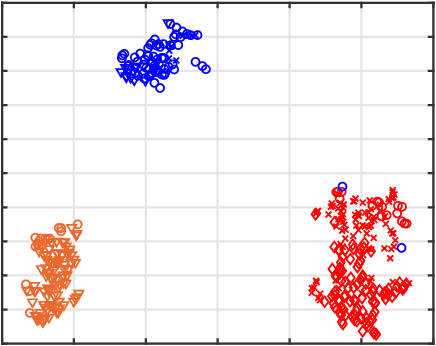
We describe a method for simultaneous visualization of multiple pairwise distances in 3 dimensional (3D) space. Given the distance matrices that correspond to 2 dimensional projections of a 3 dimensional object (dataset) the goal is to recover the 3 dimensional object (dataset). We propose an approach that uses 3D to place the points, along with projections (planes) that preserve each of the given distance matrices. Our multi-perspective, simultaneous embedding (MPSE) method is based on non-linear dimensionality reduction that generalizes multidimensional scaling. We consider two versions of the problem: in the first one we are given the input distance matrices and the projections (e.g., if we have 3 different projections we can use the three orthogonal directions of the unit cube). In the second version of the problem we also compute the best projections as part of the optimization. We experimentally evaluate MPSE using synthetic datasets that illustrate the quality of the resulting solutions. Finally, we provide a functional prototype which implements both settings.

Prediction of Dynamical time Series Using Kernel Based Regression and Smooth Splines

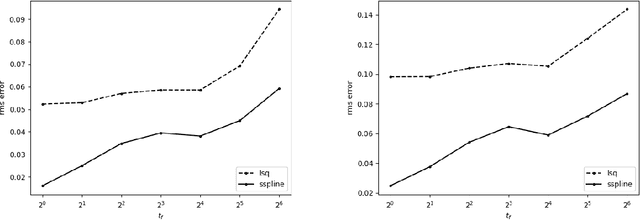
Prediction of dynamical time series with additive noise using support vector machines or kernel based regression has been proved to be consistent for certain classes of discrete dynamical systems. Consistency implies that these methods are effective at computing the expected value of a point at a future time given the present coordinates. However, the present coordinates themselves are noisy, and therefore, these methods are not necessarily effective at removing noise. In this article, we consider denoising and prediction as separate problems for flows, as opposed to discrete time dynamical systems, and show that the use of smooth splines is more effective at removing noise. Combination of smooth splines and kernel based regression yields predictors that are more accurate on benchmarks typically by a factor of 2 or more. We prove that kernel based regression in combination with smooth splines converges to the exact predictor for time series extracted from any compact invariant set of any sufficiently smooth flow. As a consequence of convergence, one can find examples where the combination of kernel based regression with smooth splines is superior by even a factor of $100$. The predictors that we compute operate on delay coordinate data and not the full state vector, which is typically not observable.