Analyzing Local Representations of Self-supervised Vision Transformers

In this paper, we present a comparative analysis of various self-supervised Vision Transformers (ViTs), focusing on their local representative power. Inspired by large language models, we examine the abilities of ViTs to perform various computer vision tasks with little to no fine-tuning. We design an evaluation framework to analyze the quality of local, i.e. patch-level, representations in the context of few-shot semantic segmentation, instance identification, object retrieval, and tracking. We discover that contrastive learning based methods like DINO produce more universal patch representations that can be immediately applied for downstream tasks with no parameter tuning, compared to masked image modeling. The embeddings learned using the latter approach, e.g. in masked autoencoders, have high variance features that harm distance-based algorithms, such as k-NN, and do not contain useful information for most downstream tasks. Furthermore, we demonstrate that removing these high-variance features enhances k-NN by providing an analysis of the benchmarks for this work and for Scale-MAE, a recent extension of masked autoencoders. Finally, we find an object instance retrieval setting where DINOv2, a model pretrained on two orders of magnitude more data, performs worse than its less compute-intensive counterpart DINO.

Balancing between the Local and Global Structures (LGS) in Graph Embedding

We present a method for balancing between the Local and Global Structures (LGS) in graph embedding, via a tunable parameter. Some embedding methods aim to capture global structures, while others attempt to preserve local neighborhoods. Few methods attempt to do both, and it is not always possible to capture well both local and global information in two dimensions, which is where most graph drawing live. The choice of using a local or a global embedding for visualization depends not only on the task but also on the structure of the underlying data, which may not be known in advance. For a given graph, LGS aims to find a good balance between the local and global structure to preserve. We evaluate the performance of LGS with synthetic and real-world datasets and our results indicate that it is competitive with the state-of-the-art methods, using established quality metrics such as stress and neighborhood preservation. We introduce a novel quality metric, cluster distance preservation, to assess intermediate structure capture. All source-code, datasets, experiments and analysis are available online.

Embedding Neighborhoods Simultaneously t-SNE (ENS-t-SNE)

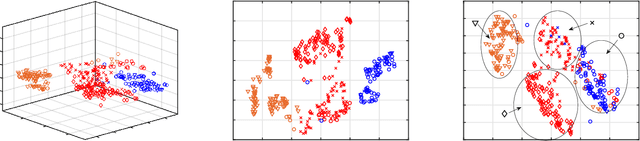
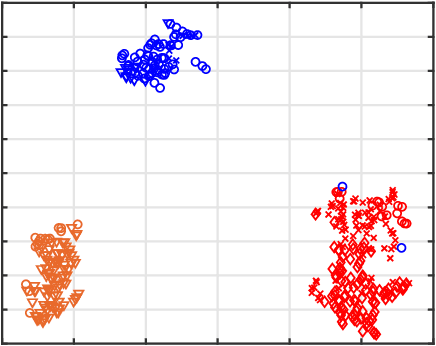
We propose an algorithm for visualizing a dataset by embedding it in 3-dimensional Euclidean space based on various given distances between the same pairs of datapoints. Its aim is to find an Embedding which preserves Neighborhoods Simultaneously for all given distances by generalizing the t-Stochastic Neighborhood Embedding approach (ENS-t-SNE). We illustrate the utility of ENS-t-SNE by demonstrating its use in three applications. First, to visualize different notions of clusters and groups within the same high-dimensional dataset with one 3-dimensional embedding, as opposed to providing different embeddings of the same data and trying to match the corresponding points. Second, to illustrate the effects of different hyper-parameters of the classical t-SNE. Third, by considering multiple different notions of clustering in data, ENS-t-SNE can generate an alternative embedding than the classic t-SNE. We provide an extensive quantitative evaluation with real-world and synthetic datasets of different sizes and using different numbers of projections.

Multi-Perspective, Simultaneous Embedding

We describe a method for simultaneous visualization of multiple pairwise distances in 3 dimensional (3D) space. Given the distance matrices that correspond to 2 dimensional projections of a 3 dimensional object (dataset) the goal is to recover the 3 dimensional object (dataset). We propose an approach that uses 3D to place the points, along with projections (planes) that preserve each of the given distance matrices. Our multi-perspective, simultaneous embedding (MPSE) method is based on non-linear dimensionality reduction that generalizes multidimensional scaling. We consider two versions of the problem: in the first one we are given the input distance matrices and the projections (e.g., if we have 3 different projections we can use the three orthogonal directions of the unit cube). In the second version of the problem we also compute the best projections as part of the optimization. We experimentally evaluate MPSE using synthetic datasets that illustrate the quality of the resulting solutions. Finally, we provide a functional prototype which implements both settings.

Solving Jigsaw Puzzles By the Graph Connection Laplacian

We propose a novel mathematical framework to address the problem of automatically solving large jigsaw puzzles. This problem assumes a large image which is cut into equal square pieces that are arbitrarily rotated and shifted and asks to recover the original image given the transformed pieces. The main contribution of this work is a theoretically-guaranteed method for recovering the unknown orientations of the puzzle pieces by using the graph connection Laplacian associated with the puzzle. Iterative application of this method and other methods for recovering the unknown shifts result in a solution for the large jigsaw puzzle problem. This solution is not greedy, unlike many other solutions. Numerical experiments demonstrate the competitive performance of the proposed method.

Distributed Robust Subspace Recovery

We propose distributed solutions to the problem of Robust Subspace Recovery (RSR). Our setting assumes a huge dataset in an ad hoc network without a central processor, where each node has access only to one chunk of the dataset. Furthermore, part of the whole dataset lies around a low-dimensional subspace and the other part is composed of outliers that lie away from that subspace. The goal is to recover the underlying subspace for the whole dataset, without transferring the data itself between the nodes. We first apply the Consensus-Based Gradient method to the Geometric Median Subspace algorithm for RSR. For this purpose, we propose an iterative solution for the local dual minimization problem and establish its r-linear convergence. We then explain how to distributedly implement the Reaper and Fast Median Subspace algorithms for RSR. The proposed algorithms display competitive performance on both synthetic and real data.