Persistent Classification: A New Approach to Stability of Data and Adversarial Examples

There are a number of hypotheses underlying the existence of adversarial examples for classification problems. These include the high-dimensionality of the data, high codimension in the ambient space of the data manifolds of interest, and that the structure of machine learning models may encourage classifiers to develop decision boundaries close to data points. This article proposes a new framework for studying adversarial examples that does not depend directly on the distance to the decision boundary. Similarly to the smoothed classifier literature, we define a (natural or adversarial) data point to be $(\gamma,\sigma)$-stable if the probability of the same classification is at least $\gamma$ for points sampled in a Gaussian neighborhood of the point with a given standard deviation $\sigma$. We focus on studying the differences between persistence metrics along interpolants of natural and adversarial points. We show that adversarial examples have significantly lower persistence than natural examples for large neural networks in the context of the MNIST and ImageNet datasets. We connect this lack of persistence with decision boundary geometry by measuring angles of interpolants with respect to decision boundaries. Finally, we connect this approach with robustness by developing a manifold alignment gradient metric and demonstrating the increase in robustness that can be achieved when training with the addition of this metric.

Manifold learning in Wasserstein space

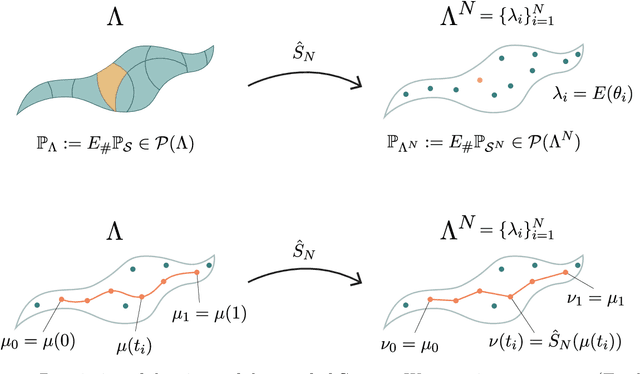
This paper aims at building the theoretical foundations for manifold learning algorithms in the space of absolutely continuous probability measures on a compact and convex subset of $\mathbb{R}^d$, metrized with the Wasserstein-2 distance $W$. We begin by introducing a natural construction of submanifolds $\Lambda$ of probability measures equipped with metric $W_\Lambda$, the geodesic restriction of $W$ to $\Lambda$. In contrast to other constructions, these submanifolds are not necessarily flat, but still allow for local linearizations in a similar fashion to Riemannian submanifolds of $\mathbb{R}^d$. We then show how the latent manifold structure of $(\Lambda,W_{\Lambda})$ can be learned from samples $\{\lambda_i\}_{i=1}^N$ of $\Lambda$ and pairwise extrinsic Wasserstein distances $W$ only. In particular, we show that the metric space $(\Lambda,W_{\Lambda})$ can be asymptotically recovered in the sense of Gromov--Wasserstein from a graph with nodes $\{\lambda_i\}_{i=1}^N$ and edge weights $W(\lambda_i,\lambda_j)$. In addition, we demonstrate how the tangent space at a sample $\lambda$ can be asymptotically recovered via spectral analysis of a suitable "covariance operator" using optimal transport maps from $\lambda$ to sufficiently close and diverse samples $\{\lambda_i\}_{i=1}^N$. The paper closes with some explicit constructions of submanifolds $\Lambda$ and numerical examples on the recovery of tangent spaces through spectral analysis.

Lattice Approximations in Wasserstein Space

We consider structured approximation of measures in Wasserstein space $W_p(\mathbb{R}^d)$ for $p\in[1,\infty)$ by discrete and piecewise constant measures based on a scaled Voronoi partition of $\mathbb{R}^d$. We show that if a full rank lattice $\Lambda$ is scaled by a factor of $h\in(0,1]$, then approximation of a measure based on the Voronoi partition of $h\Lambda$ is $O(h)$ regardless of $d$ or $p$. We then use a covering argument to show that $N$-term approximations of compactly supported measures is $O(N^{-\frac1d})$ which matches known rates for optimal quantizers and empirical measure approximation in most instances. Finally, we extend these results to noncompactly supported measures with sufficient decay.

On Wasserstein distances for affine transformations of random vectors

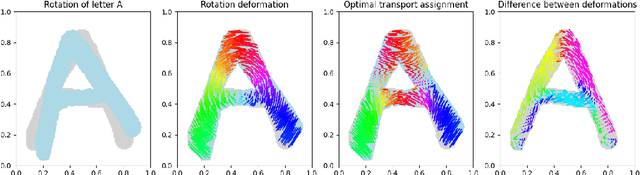
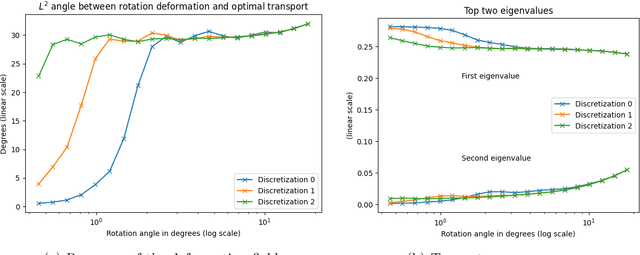
We expound on some known lower bounds of the quadratic Wasserstein distance between random vectors in $\mathbb{R}^n$ with an emphasis on affine transformations that have been used in manifold learning of data in Wasserstein space. In particular, we give concrete lower bounds for rotated copies of random vectors in $\mathbb{R}^2$ with uncorrelated components by computing the Bures metric between the covariance matrices. We also derive upper bounds for compositions of affine maps which yield a fruitful variety of diffeomorphisms applied to an initial data measure. We apply these bounds to various distributions including those lying on a 1-dimensional manifold in $\mathbb{R}^2$ and illustrate the quality of the bounds. Finally, we give a framework for mimicking handwritten digit or alphabet datasets that can be applied in a manifold learning framework.

Boosting Nyström Method

The Nystr\"{o}m method is an effective tool to generate low-rank approximations of large matrices, and it is particularly useful for kernel-based learning. To improve the standard Nystr\"{o}m approximation, ensemble Nystr\"{o}m algorithms compute a mixture of Nystr\"{o}m approximations which are generated independently based on column resampling. We propose a new family of algorithms, boosting Nystr\"{o}m, which iteratively generate multiple ``weak'' Nystr\"{o}m approximations (each using a small number of columns) in a sequence adaptively - each approximation aims to compensate for the weaknesses of its predecessor - and then combine them to form one strong approximation. We demonstrate that our boosting Nystr\"{o}m algorithms can yield more efficient and accurate low-rank approximations to kernel matrices. Improvements over the standard and ensemble Nystr\"{o}m methods are illustrated by simulation studies and real-world data analysis.

Linearized Wasserstein dimensionality reduction with approximation guarantees

We introduce LOT Wassmap, a computationally feasible algorithm to uncover low-dimensional structures in the Wasserstein space. The algorithm is motivated by the observation that many datasets are naturally interpreted as probability measures rather than points in $\mathbb{R}^n$, and that finding low-dimensional descriptions of such datasets requires manifold learning algorithms in the Wasserstein space. Most available algorithms are based on computing the pairwise Wasserstein distance matrix, which can be computationally challenging for large datasets in high dimensions. Our algorithm leverages approximation schemes such as Sinkhorn distances and linearized optimal transport to speed-up computations, and in particular, avoids computing a pairwise distance matrix. We provide guarantees on the embedding quality under such approximations, including when explicit descriptions of the probability measures are not available and one must deal with finite samples instead. Experiments demonstrate that LOT Wassmap attains correct embeddings and that the quality improves with increased sample size. We also show how LOT Wassmap significantly reduces the computational cost when compared to algorithms that depend on pairwise distance computations.

Riemannian CUR Decompositions for Robust Principal Component Analysis

Robust Principal Component Analysis (PCA) has received massive attention in recent years. It aims to recover a low-rank matrix and a sparse matrix from their sum. This paper proposes a novel nonconvex Robust PCA algorithm, coined Riemannian CUR (RieCUR), which utilizes the ideas of Riemannian optimization and robust CUR decompositions. This algorithm has the same computational complexity as Iterated Robust CUR, which is currently state-of-the-art, but is more robust to outliers. RieCUR is also able to tolerate a significant amount of outliers, and is comparable to Accelerated Alternating Projections, which has high outlier tolerance but worse computational complexity than the proposed method. Thus, the proposed algorithm achieves state-of-the-art performance on Robust PCA both in terms of computational complexity and outlier tolerance.

Wassmap: Wasserstein Isometric Mapping for Image Manifold Learning

In this paper, we propose Wasserstein Isometric Mapping (Wassmap), a parameter-free nonlinear dimensionality reduction technique that provides solutions to some drawbacks in existing global nonlinear dimensionality reduction algorithms in imaging applications. Wassmap represents images via probability measures in Wasserstein space, then uses pairwise quadratic Wasserstein distances between the associated measures to produce a low-dimensional, approximately isometric embedding. We show that the algorithm is able to exactly recover parameters of some image manifolds including those generated by translations or dilations of a fixed generating measure. Additionally, we show that a discrete version of the algorithm retrieves parameters from manifolds generated from discrete measures by providing a theoretical bridge to transfer recovery results from functional data to discrete data. Testing of the proposed algorithms on various image data manifolds show that Wassmap yields good embeddings compared with other global techniques.

Computing Steiner Trees using Graph Neural Networks

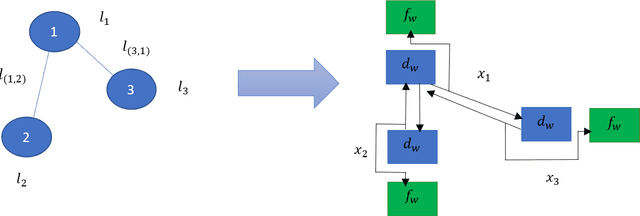
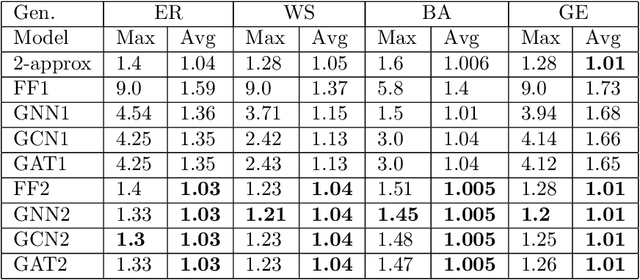
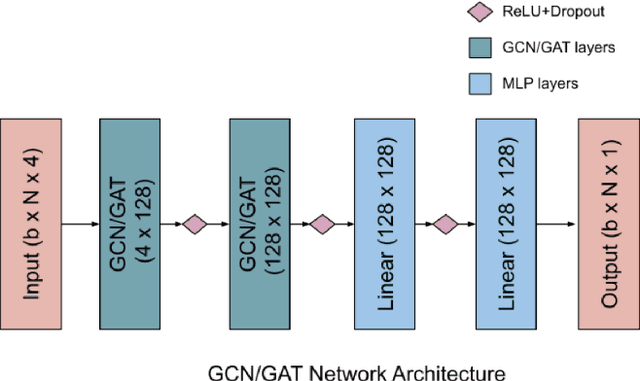
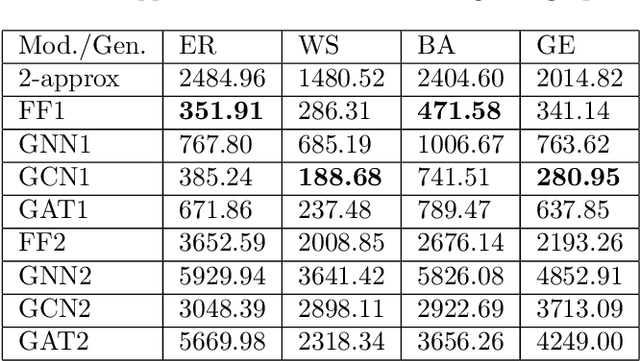
Graph neural networks have been successful in many learning problems and real-world applications. A recent line of research explores the power of graph neural networks to solve combinatorial and graph algorithmic problems such as subgraph isomorphism, detecting cliques, and the traveling salesman problem. However, many NP-complete problems are as of yet unexplored using this method. In this paper, we tackle the Steiner Tree Problem. We employ four learning frameworks to compute low cost Steiner trees: feed-forward neural networks, graph neural networks, graph convolutional networks, and a graph attention model. We use these frameworks in two fundamentally different ways: 1) to train the models to learn the actual Steiner tree nodes, 2) to train the model to learn good Steiner point candidates to be connected to the constructed tree using a shortest path in a greedy fashion. We illustrate the robustness of our heuristics on several random graph generation models as well as the SteinLib data library. Our finding suggests that the out-of-the-box application of GNN methods does worse than the classic 2-approximation method. However, when combined with a greedy shortest path construction, it even does slightly better than the 2-approximation algorithm. This result sheds light on the fundamental capabilities and limitations of graph learning techniques on classical NP-complete problems.

On Matrix Factorizations in Subspace Clustering

This article explores subspace clustering algorithms using CUR decompositions, and examines the effect of various hyperparameters in these algorithms on clustering performance on two real-world benchmark datasets, the Hopkins155 motion segmentation dataset and the Yale face dataset. Extensive experiments are done for a variety of sampling methods and oversampling parameters for these datasets, and some guidelines for parameter choices are given for practical applications.