Transfer Operators from Batches of Unpaired Points via Entropic Transport Kernels

In this paper, we are concerned with estimating the joint probability of random variables $X$ and $Y$, given $N$ independent observation blocks $(\boldsymbol{x}^i,\boldsymbol{y}^i)$, $i=1,\ldots,N$, each of $M$ samples $(\boldsymbol{x}^i,\boldsymbol{y}^i) = \bigl((x^i_j, y^i_{\sigma^i(j)}) \bigr)_{j=1}^M$, where $\sigma^i$ denotes an unknown permutation of i.i.d. sampled pairs $(x^i_j,y_j^i)$, $j=1,\ldots,M$. This means that the internal ordering of the $M$ samples within an observation block is not known. We derive a maximum-likelihood inference functional, propose a computationally tractable approximation and analyze their properties. In particular, we prove a $\Gamma$-convergence result showing that we can recover the true density from empirical approximations as the number $N$ of blocks goes to infinity. Using entropic optimal transport kernels, we model a class of hypothesis spaces of density functions over which the inference functional can be minimized. This hypothesis class is particularly suited for approximate inference of transfer operators from data. We solve the resulting discrete minimization problem by a modification of the EMML algorithm to take addional transition probability constraints into account and prove the convergence of this algorithm. Proof-of-concept examples demonstrate the potential of our method.

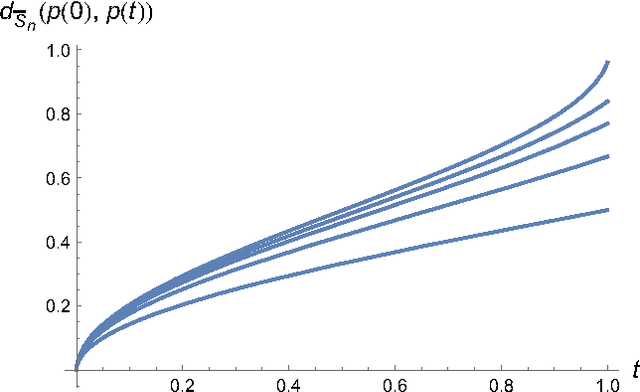
Manifold learning in Wasserstein space

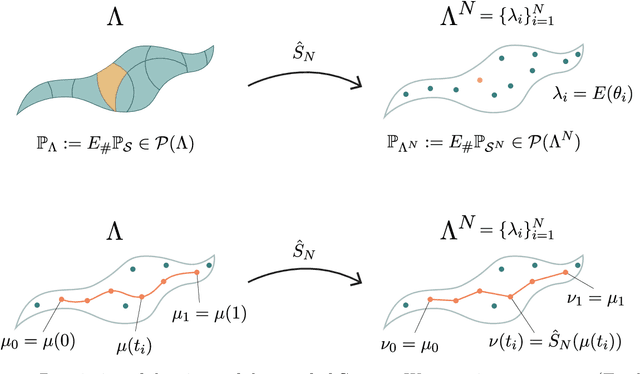
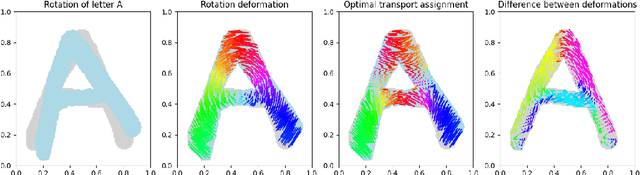
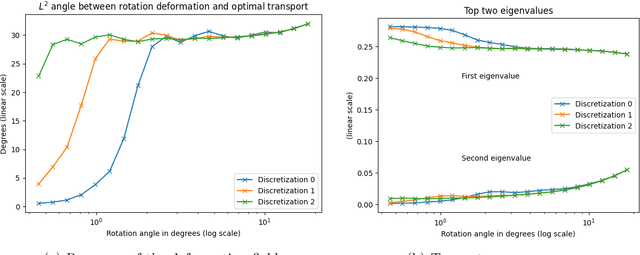
This paper aims at building the theoretical foundations for manifold learning algorithms in the space of absolutely continuous probability measures on a compact and convex subset of $\mathbb{R}^d$, metrized with the Wasserstein-2 distance $W$. We begin by introducing a natural construction of submanifolds $\Lambda$ of probability measures equipped with metric $W_\Lambda$, the geodesic restriction of $W$ to $\Lambda$. In contrast to other constructions, these submanifolds are not necessarily flat, but still allow for local linearizations in a similar fashion to Riemannian submanifolds of $\mathbb{R}^d$. We then show how the latent manifold structure of $(\Lambda,W_{\Lambda})$ can be learned from samples $\{\lambda_i\}_{i=1}^N$ of $\Lambda$ and pairwise extrinsic Wasserstein distances $W$ only. In particular, we show that the metric space $(\Lambda,W_{\Lambda})$ can be asymptotically recovered in the sense of Gromov--Wasserstein from a graph with nodes $\{\lambda_i\}_{i=1}^N$ and edge weights $W(\lambda_i,\lambda_j)$. In addition, we demonstrate how the tangent space at a sample $\lambda$ can be asymptotically recovered via spectral analysis of a suitable "covariance operator" using optimal transport maps from $\lambda$ to sufficiently close and diverse samples $\{\lambda_i\}_{i=1}^N$. The paper closes with some explicit constructions of submanifolds $\Lambda$ and numerical examples on the recovery of tangent spaces through spectral analysis.

Dynamic Cell Imaging in PET with Optimal Transport Regularization

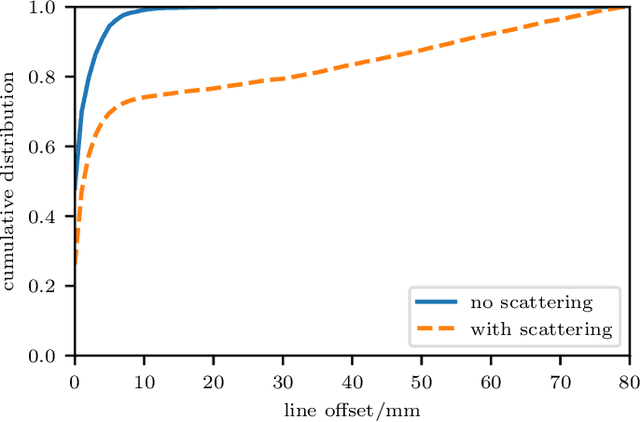
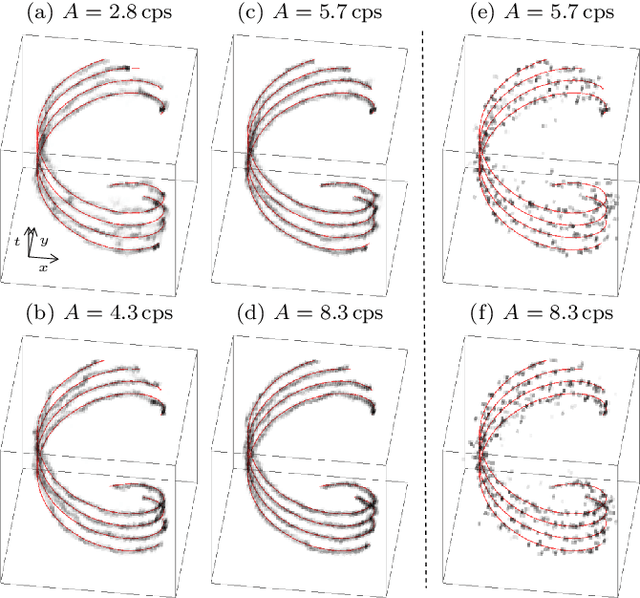
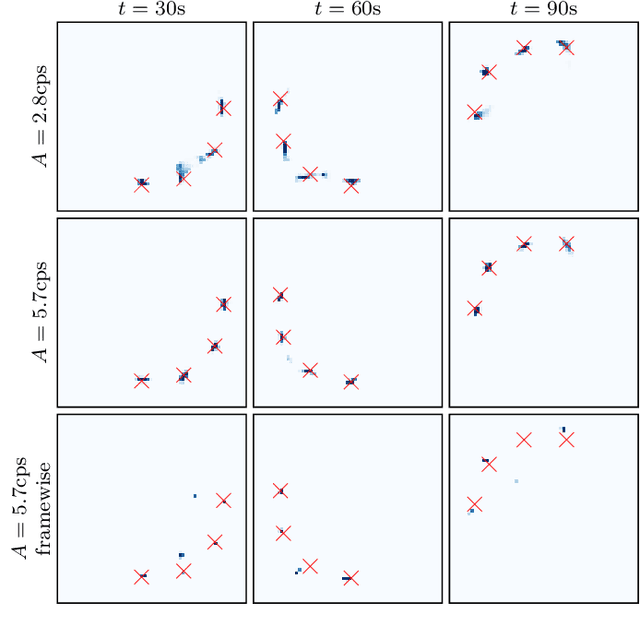
We propose a novel dynamic image reconstruction method from PET listmode data that could be particularly suited to tracking single or small numbers of cells. In contrast to conventional PET reconstruction the proposed method combines the information from all detected events not only to reconstruct the dynamic evolution of the radionuclide distribution, but also to simultaneously improve the reconstruction at each single time point by enforcing temporal consistency. This is achieved via the use of optimal transport regularization where in principle, among all possible temporally evolving radionuclide distributions consistent with the PET measurement, the one is chosen with least kinetic motion energy. The reconstruction is found by convex optimization so that there is no dependence on the initialization of the method. We study its behaviour on simulated data of a human PET system and demonstrate its robustness even in settings with very low radioactivity. In contrast to previously reported cell tracking algorithms, the proposed technique is oblivious to the number of tracked cells. Without any additional complexity one or multiple cells can be reconstructed, and the model automatically determines the number of particles. As one of the results, four radiolabelled cells moving with a velocity of 3.1 mm/s and a PET recorded count rate of 1.1 cps (for each cell) could be simultaneously tracked with a tracking accuracy of 5.4 mm inside a simulated human body.

A Framework for Wasserstein-1-Type Metrics

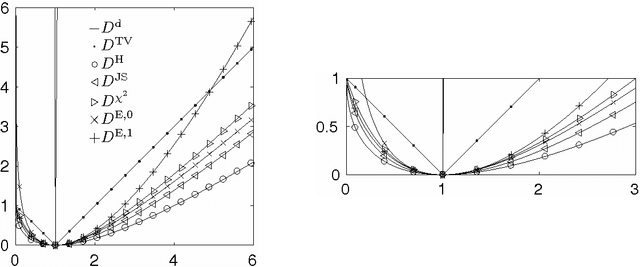
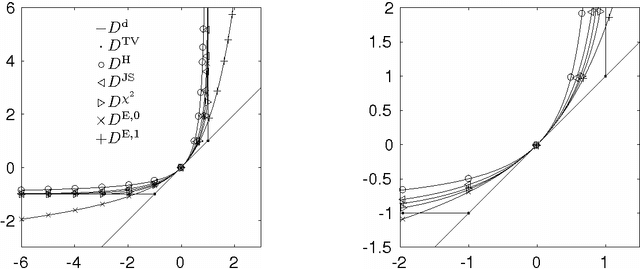
We propose a unifying framework for generalising the Wasserstein-1 metric to a discrepancy measure between nonnegative measures of different mass. This generalization inherits the convexity and computational efficiency from the Wasserstein-1 metric, and it includes several previous approaches from the literature as special cases. For various specific instances of the generalized Wasserstein-1 metric we furthermore demonstrate their usefulness in applications by numerical experiments.

Image Labeling by Assignment

We introduce a novel geometric approach to the image labeling problem. Abstracting from specific labeling applications, a general objective function is defined on a manifold of stochastic matrices, whose elements assign prior data that are given in any metric space, to observed image measurements. The corresponding Riemannian gradient flow entails a set of replicator equations, one for each data point, that are spatially coupled by geometric averaging on the manifold. Starting from uniform assignments at the barycenter as natural initialization, the flow terminates at some global maximum, each of which corresponds to an image labeling that uniquely assigns the prior data. Our geometric variational approach constitutes a smooth non-convex inner approximation of the general image labeling problem, implemented with sparse interior-point numerics in terms of parallel multiplicative updates that converge efficiently.

Globally Optimal Joint Image Segmentation and Shape Matching Based on Wasserstein Modes

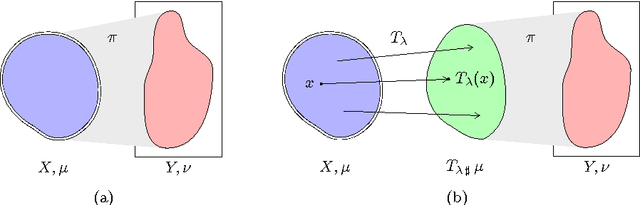
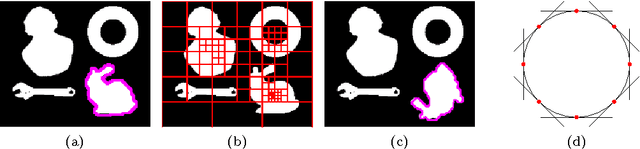
A functional for joint variational object segmentation and shape matching is developed. The formulation is based on optimal transport w.r.t. geometric distance and local feature similarity. Geometric invariance and modelling of object-typical statistical variations is achieved by introducing degrees of freedom that describe transformations and deformations of the shape template. The shape model is mathematically equivalent to contour-based approaches but inference can be performed without conversion between the contour and region representations, allowing combination with other convex segmentation approaches and simplifying optimization. While the overall functional is non-convex, non-convexity is confined to a low-dimensional variable. We propose a locally optimal alternating optimization scheme and a globally optimal branch and bound scheme, based on adaptive convex relaxation. Combining both methods allows to eliminate the delicate initialization problem inherent to many contour based approaches while remaining computationally practical. The properties of the functional, its ability to adapt to a wide range of input data structures and the different optimization schemes are illustrated and compared by numerical experiments.

Contour Manifolds and Optimal Transport

Describing shapes by suitable measures in object segmentation, as proposed in [24], allows to combine the advantages of the representations as parametrized contours and indicator functions. The pseudo-Riemannian structure of optimal transport can be used to model shapes in ways similar as with contours, while the Kantorovich functional enables the application of convex optimization methods for global optimality of the segmentation functional. In this paper we provide a mathematical study of the shape measure representation and its relation to the contour description. In particular we show that the pseudo-Riemannian structure of optimal transport, when restricted to the set of shape measures, yields a manifold which is diffeomorphic to the manifold of closed contours. A discussion of the metric induced by optimal transport and the corresponding geodesic equation is given.