Sigma Flows for Image and Data Labeling and Learning Structured Prediction

This paper introduces the sigma flow model for the prediction of structured labelings of data observed on Riemannian manifolds, including Euclidean image domains as special case. The approach combines the Laplace-Beltrami framework for image denoising and enhancement, introduced by Sochen, Kimmel and Malladi about 25 years ago, and the assignment flow approach introduced and studied by the authors. The sigma flow arises as Riemannian gradient flow of generalized harmonic energies and thus is governed by a nonlinear geometric PDE which determines a harmonic map from a closed Riemannian domain manifold to a statistical manifold, equipped with the Fisher-Rao metric from information geometry. A specific ingredient of the sigma flow is the mutual dependency of the Riemannian metric of the domain manifold on the evolving state. This makes the approach amenable to machine learning in a specific way, by realizing this dependency through a mapping with compact time-variant parametrization that can be learned from data. Proof of concept experiments demonstrate the expressivity of the sigma flow model and prediction performance. Structural similarities to transformer network architectures and networks generated by the geometric integration of sigma flows are pointed out, which highlights the connection to deep learning and, conversely, may stimulate the use of geometric design principles for structured prediction in other areas of scientific machine learning.

Generative Assignment Flows for Representing and Learning Joint Distributions of Discrete Data

We introduce a novel generative model for the representation of joint probability distributions of a possibly large number of discrete random variables. The approach uses measure transport by randomized assignment flows on the statistical submanifold of factorizing distributions, which also enables to sample efficiently from the target distribution and to assess the likelihood of unseen data points. The embedding of the flow via the Segre map in the meta-simplex of all discrete joint distributions ensures that any target distribution can be represented in principle, whose complexity in practice only depends on the parametrization of the affinity function of the dynamical assignment flow system. Our model can be trained in a simulation-free manner without integration by conditional Riemannian flow matching, using the training data encoded as geodesics in closed-form with respect to the e-connection of information geometry. By projecting high-dimensional flow matching in the meta-simplex of joint distributions to the submanifold of factorizing distributions, our approach has strong motivation from first principles of modeling coupled discrete variables. Numerical experiments devoted to distributions of structured image labelings demonstrate the applicability to large-scale problems, which may include discrete distributions in other application areas. Performance measures show that our approach scales better with the increasing number of classes than recent related work.

Multi-level Geometric Optimization for Regularised Constrained Linear Inverse Problems

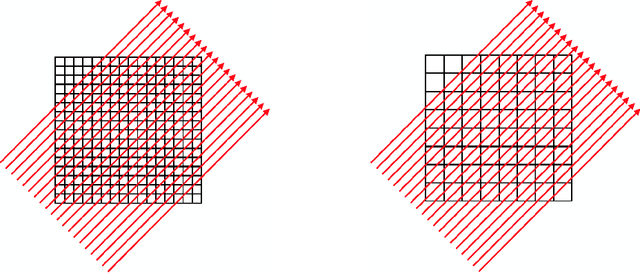
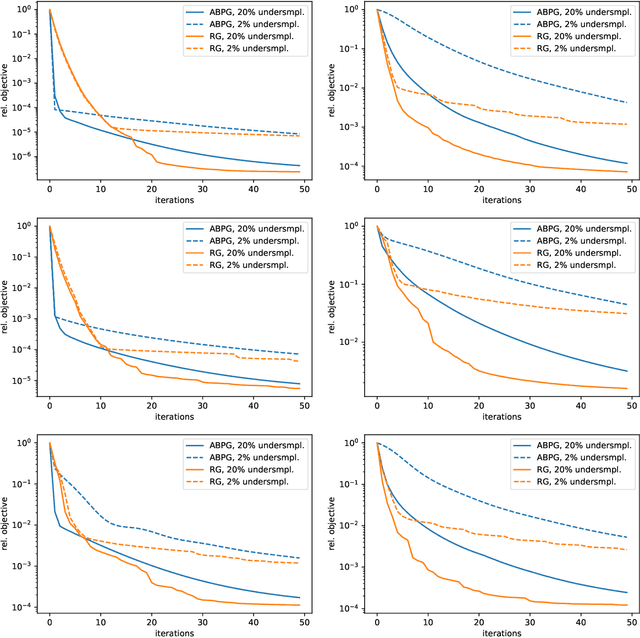
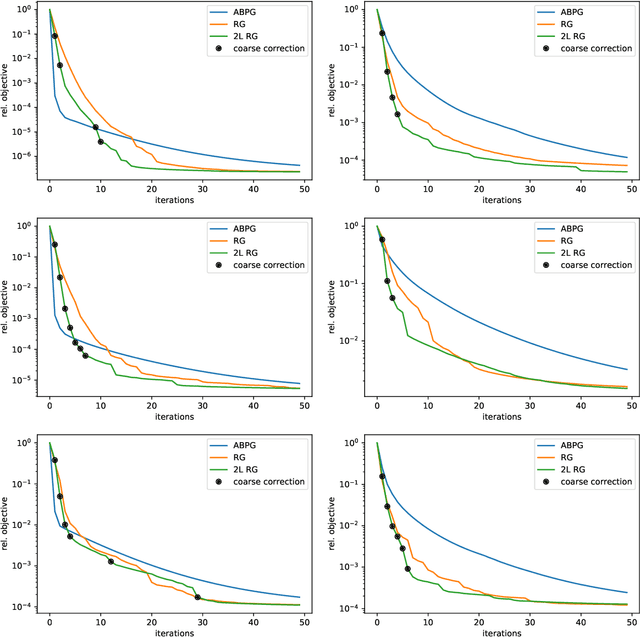
We present a geometric multi-level optimization approach that smoothly incorporates box constraints. Given a box constrained optimization problem, we consider a hierarchy of models with varying discretization levels. Finer models are accurate but expensive to compute, while coarser models are less accurate but cheaper to compute. When working at the fine level, multi-level optimisation computes the search direction based on a coarser model which speeds up updates at the fine level. Moreover, exploiting geometry induced by the hierarchy the feasibility of the updates is preserved. In particular, our approach extends classical components of multigrid methods like restriction and prolongation to the Riemannian structure of our constraints.

Self-Certifying Classification by Linearized Deep Assignment

We propose a novel class of deep stochastic predictors for classifying metric data on graphs within the PAC-Bayes risk certification paradigm. Classifiers are realized as linearly parametrized deep assignment flows with random initial conditions. Building on the recent PAC-Bayes literature and data-dependent priors, this approach enables (i) to use risk bounds as training objectives for learning posterior distributions on the hypothesis space and (ii) to compute tight out-of-sample risk certificates of randomized classifiers more efficiently than related work. Comparison with empirical test set errors illustrates the performance and practicality of this self-certifying classification method.

Learning Linearized Assignment Flows for Image Labeling

We introduce a novel algorithm for estimating optimal parameters of linearized assignment flows for image labeling. An exact formula is derived for the parameter gradient of any loss function that is constrained by the linear system of ODEs determining the linearized assignment flow. We show how to efficiently evaluate this formula using a Krylov subspace and a low-rank approximation. This enables us to perform parameter learning by Riemannian gradient descent in the parameter space, without the need to backpropagate errors or to solve an adjoint equation, in less than 10 seconds for a $512\times 512$ image using just about $0.5$ GB memory. Experiments demonstrate that our method performs as good as highly-tuned machine learning software using automatic differentiation. Unlike methods employing automatic differentiation, our approach yields a low-dimensional representation of internal parameters and their dynamics which helps to understand how networks work and perform that realize assignment flows and generalizations thereof.

Multi-Channel Potts-Based Reconstruction for Multi-Spectral Computed Tomography

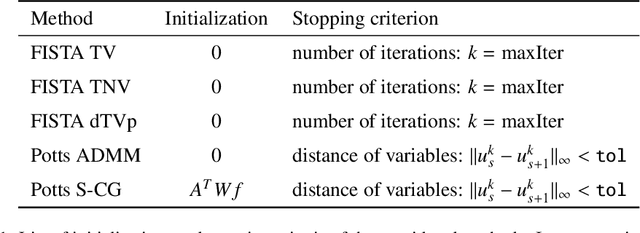
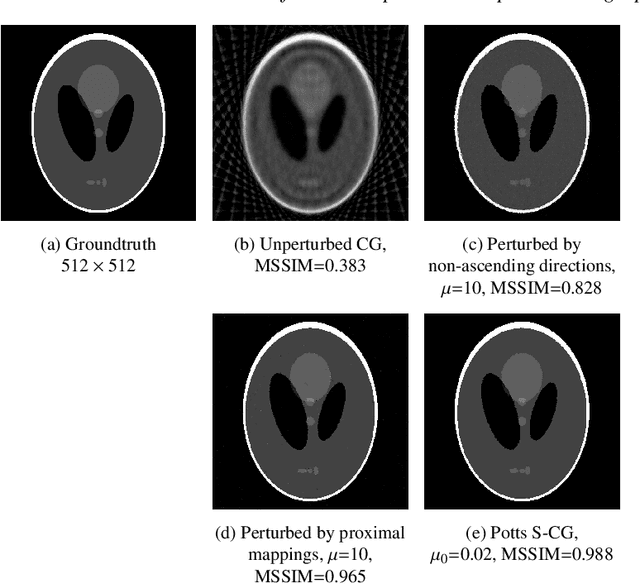
We consider reconstructing multi-channel images from measurements performed by photon-counting and energy-discriminating detectors in the setting of multi-spectral X-ray computed tomography (CT). Our aim is to exploit the strong structural correlation that is known to exist between the channels of multi-spectral CT images. To that end, we adopt the multi-channel Potts prior to jointly reconstruct all channels. This prior produces piecewise constant solutions with strongly correlated channels. In particular, edges are enforced to have the same spatial position across channels which is a benefit over TV-based methods. We consider the Potts prior in two frameworks: (a) in the context of a variational Potts model, and (b) in a Potts-superiorization approach that perturbs the iterates of a basic iterative least squares solver. We identify an alternating direction method of multipliers (ADMM) approach as well as a Potts-superiorized conjugate gradient method as particularly suitable. In numerical experiments, we compare the Potts prior based approaches to existing TV-type approaches on realistically simulated multi-spectral CT data and obtain improved reconstruction for compound solid bodies.

Self-Assignment Flows for Unsupervised Data Labeling on Graphs

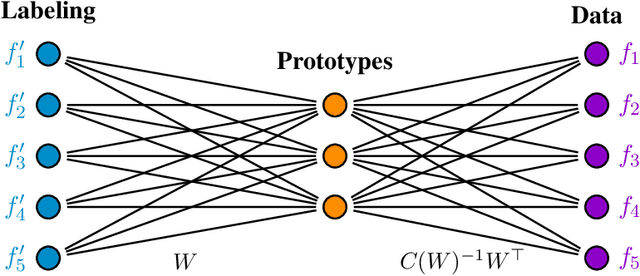
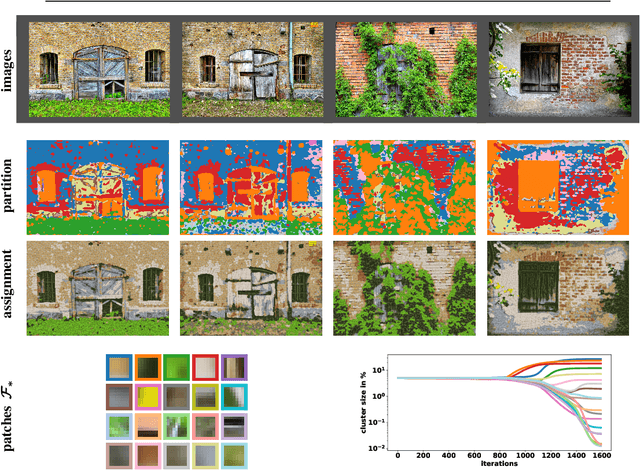
This paper extends the recently introduced assignment flow approach for supervised image labeling to unsupervised scenarios where no labels are given. The resulting self-assignment flow takes a pairwise data affinity matrix as input data and maximizes the correlation with a low-rank matrix that is parametrized by the variables of the assignment flow, which entails an assignment of the data to themselves through the formation of latent labels (feature prototypes). A single user parameter, the neighborhood size for the geometric regularization of assignments, drives the entire process. By smooth geodesic interpolation between different normalizations of self-assignment matrices on the positive definite matrix manifold, a one-parameter family of self-assignment flows is defined. Accordingly, our approach can be characterized from different viewpoints, e.g. as performing spatially regularized, rank-constrained discrete optimal transport, or as computing spatially regularized normalized spectral cuts. Regarding combinatorial optimization, our approach successfully determines completely positive factorizations of self-assignments in large-scale scenarios, subject to spatial regularization. Various experiments including the unsupervised learning of patch dictionaries using a locally invariant distance function, illustrate the properties of the approach.

Learning Adaptive Regularization for Image Labeling Using Geometric Assignment

We study the inverse problem of model parameter learning for pixelwise image labeling, using the linear assignment flow and training data with ground truth. This is accomplished by a Riemannian gradient flow on the manifold of parameters that determine the regularization properties of the assignment flow. Using the symplectic partitioned Runge--Kutta method for numerical integration, it is shown that deriving the sensitivity conditions of the parameter learning problem and its discretization commute. A convenient property of our approach is that learning is based on exact inference. Carefully designed experiments demonstrate the performance of our approach, the expressiveness of the mathematical model as well as its limitations, from the viewpoint of statistical learning and optimal control.

Unsupervised Assignment Flow: Label Learning on Feature Manifolds by Spatially Regularized Geometric Assignment

This paper introduces the unsupervised assignment flow that couples the assignment flow for supervised image labeling with Riemannian gradient flows for label evolution on feature manifolds. The latter component of the approach encompasses extensions of state-of-the-art clustering approaches to manifold-valued data. Coupling label evolution with the spatially regularized assignment flow induces a sparsifying effect that enables to learn compact label dictionaries in an unsupervised manner. Our approach alleviates the requirement for supervised labeling to have proper labels at hand, because an initial set of labels can evolve and adapt to better values while being assigned to given data. The separation between feature and assignment manifolds enables the flexible application which is demonstrated for three scenarios with manifold-valued features. Experiments demonstrate beneficial effect in both directions: adaptivity of labels improves image labeling, and steering label evolution by spatially regularized assignments leads to proper labels, because the assignment flow for supervised labeling is exactly used without any approximation for label learning.

Image Labeling by Assignment

We introduce a novel geometric approach to the image labeling problem. Abstracting from specific labeling applications, a general objective function is defined on a manifold of stochastic matrices, whose elements assign prior data that are given in any metric space, to observed image measurements. The corresponding Riemannian gradient flow entails a set of replicator equations, one for each data point, that are spatially coupled by geometric averaging on the manifold. Starting from uniform assignments at the barycenter as natural initialization, the flow terminates at some global maximum, each of which corresponds to an image labeling that uniquely assigns the prior data. Our geometric variational approach constitutes a smooth non-convex inner approximation of the general image labeling problem, implemented with sparse interior-point numerics in terms of parallel multiplicative updates that converge efficiently.