Multi-Channel Potts-Based Reconstruction for Multi-Spectral Computed Tomography

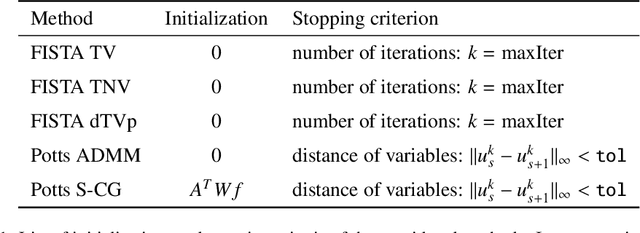
We consider reconstructing multi-channel images from measurements performed by photon-counting and energy-discriminating detectors in the setting of multi-spectral X-ray computed tomography (CT). Our aim is to exploit the strong structural correlation that is known to exist between the channels of multi-spectral CT images. To that end, we adopt the multi-channel Potts prior to jointly reconstruct all channels. This prior produces piecewise constant solutions with strongly correlated channels. In particular, edges are enforced to have the same spatial position across channels which is a benefit over TV-based methods. We consider the Potts prior in two frameworks: (a) in the context of a variational Potts model, and (b) in a Potts-superiorization approach that perturbs the iterates of a basic iterative least squares solver. We identify an alternating direction method of multipliers (ADMM) approach as well as a Potts-superiorized conjugate gradient method as particularly suitable. In numerical experiments, we compare the Potts prior based approaches to existing TV-type approaches on realistically simulated multi-spectral CT data and obtain improved reconstruction for compound solid bodies.

Iterative Potts minimization for the recovery of signals with discontinuities from indirect measurements -- the multivariate case

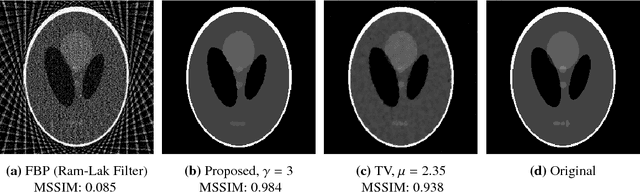
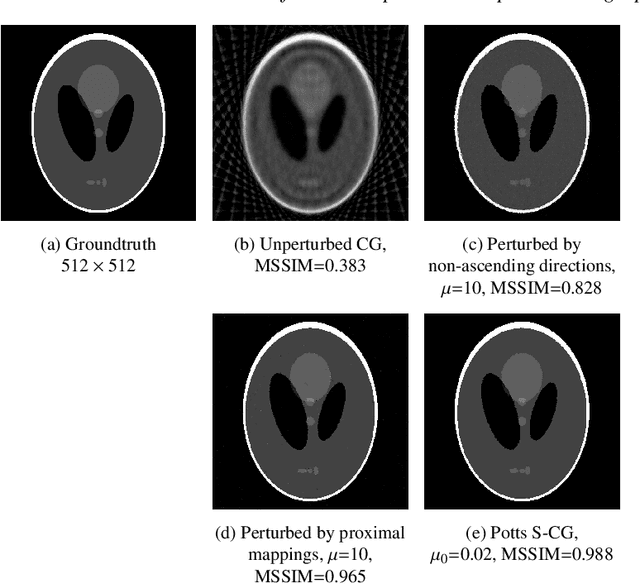
Signals and images with discontinuities appear in many problems in such diverse areas as biology, medicine, mechanics, and electrical engineering. The concrete data are often discrete, indirect and noisy measurements of some quantities describing the signal under consideration. A frequent task is to find the segments of the signal or image which corresponds to finding the discontinuities or jumps in the data. Methods based on minimizing the piecewise constant Mumford-Shah functional -- whose discretized version is known as Potts functional -- are advantageous in this scenario, in particular, in connection with segmentation. However, due to their non-convexity, minimization of such functionals is challenging. In this paper we propose a new iterative minimization strategy for the multivariate Potts functional dealing with indirect, noisy measurements. We provide a convergence analysis and underpin our findings with numerical experiments.