Martin Storath
Low-Dose CT Image Reconstruction by Fine-Tuning a UNet Pretrained for Gaussian Denoising for the Downstream Task of Image Enhancement
Mar 06, 2024Abstract:Computed Tomography (CT) is a widely used medical imaging modality, and as it is based on ionizing radiation, it is desirable to minimize the radiation dose. However, a reduced radiation dose comes with reduced image quality, and reconstruction from low-dose CT (LDCT) data is still a challenging task which is subject to research. According to the LoDoPaB-CT benchmark, a benchmark for LDCT reconstruction, many state-of-the-art methods use pipelines involving UNet-type architectures. Specifically the top ranking method, ItNet, employs a three-stage process involving filtered backprojection (FBP), a UNet trained on CT data, and an iterative refinement step. In this paper, we propose a less complex two-stage method. The first stage also employs FBP, while the novelty lies in the training strategy for the second stage, characterized as the CT image enhancement stage. The crucial point of our approach is that the neural network is pretrained on a distinctly different pretraining task with non-CT data, namely Gaussian noise removal on a variety of natural grayscale images (photographs). We then fine-tune this network for the downstream task of CT image enhancement using pairs of LDCT images and corresponding normal-dose CT images (NDCT). Despite being notably simpler than the state-of-the-art, as the pretraining did not depend on domain-specific CT data and no further iterative refinement step was necessary, the proposed two-stage method achieves competitive results. The proposed method achieves a shared top ranking in the LoDoPaB-CT challenge and a first position with respect to the SSIM metric.
Multi-Channel Potts-Based Reconstruction for Multi-Spectral Computed Tomography
Sep 12, 2020

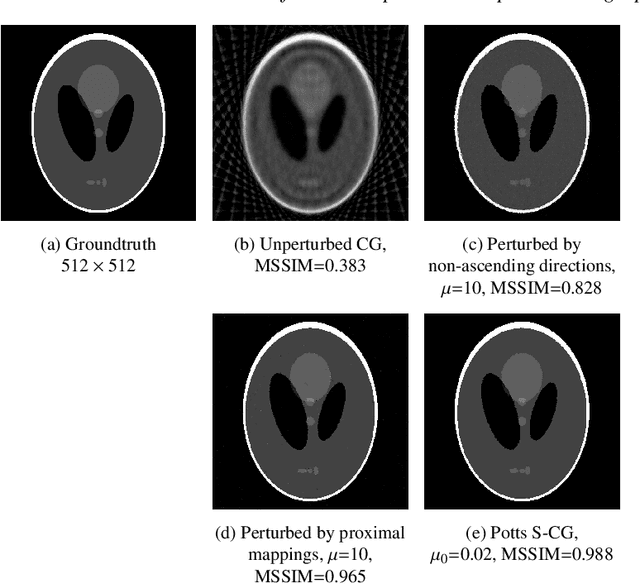
Abstract:We consider reconstructing multi-channel images from measurements performed by photon-counting and energy-discriminating detectors in the setting of multi-spectral X-ray computed tomography (CT). Our aim is to exploit the strong structural correlation that is known to exist between the channels of multi-spectral CT images. To that end, we adopt the multi-channel Potts prior to jointly reconstruct all channels. This prior produces piecewise constant solutions with strongly correlated channels. In particular, edges are enforced to have the same spatial position across channels which is a benefit over TV-based methods. We consider the Potts prior in two frameworks: (a) in the context of a variational Potts model, and (b) in a Potts-superiorization approach that perturbs the iterates of a basic iterative least squares solver. We identify an alternating direction method of multipliers (ADMM) approach as well as a Potts-superiorized conjugate gradient method as particularly suitable. In numerical experiments, we compare the Potts prior based approaches to existing TV-type approaches on realistically simulated multi-spectral CT data and obtain improved reconstruction for compound solid bodies.
Iterative Potts minimization for the recovery of signals with discontinuities from indirect measurements -- the multivariate case
Dec 03, 2018


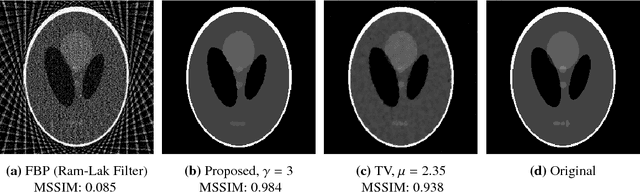
Abstract:Signals and images with discontinuities appear in many problems in such diverse areas as biology, medicine, mechanics, and electrical engineering. The concrete data are often discrete, indirect and noisy measurements of some quantities describing the signal under consideration. A frequent task is to find the segments of the signal or image which corresponds to finding the discontinuities or jumps in the data. Methods based on minimizing the piecewise constant Mumford-Shah functional -- whose discretized version is known as Potts functional -- are advantageous in this scenario, in particular, in connection with segmentation. However, due to their non-convexity, minimization of such functionals is challenging. In this paper we propose a new iterative minimization strategy for the multivariate Potts functional dealing with indirect, noisy measurements. We provide a convergence analysis and underpin our findings with numerical experiments.
Wavelet Sparse Regularization for Manifold-Valued Data
Aug 01, 2018



Abstract:In this paper, we consider the sparse regularization of manifold-valued data with respect to an interpolatory wavelet/multiscale transform. We propose and study variational models for this task and provide results on their well-posedness. We present algorithms for a numerical realization of these models in the manifold setup. Further, we provide experimental results to show the potential of the proposed schemes for applications.
Variational Regularization of Inverse Problems for Manifold-Valued Data
Apr 27, 2018



Abstract:In this paper, we consider the variational regularization of manifold-valued data in the inverse problems setting. In particular, we consider TV and TGV regularization for manifold-valued data with indirect measurement operators. We provide results on the well-posedness and present algorithms for a numerical realization of these models in the manifold setup. Further, we provide experimental results for synthetic and real data to show the potential of the proposed schemes for applications.
Learning Steerable Filters for Rotation Equivariant CNNs
Mar 19, 2018



Abstract:In many machine learning tasks it is desirable that a model's prediction transforms in an equivariant way under transformations of its input. Convolutional neural networks (CNNs) implement translational equivariance by construction; for other transformations, however, they are compelled to learn the proper mapping. In this work, we develop Steerable Filter CNNs (SFCNNs) which achieve joint equivariance under translations and rotations by design. The proposed architecture employs steerable filters to efficiently compute orientation dependent responses for many orientations without suffering interpolation artifacts from filter rotation. We utilize group convolutions which guarantee an equivariant mapping. In addition, we generalize He's weight initialization scheme to filters which are defined as a linear combination of a system of atomic filters. Numerical experiments show a substantial enhancement of the sample complexity with a growing number of sampled filter orientations and confirm that the network generalizes learned patterns over orientations. The proposed approach achieves state-of-the-art on the rotated MNIST benchmark and on the ISBI 2012 2D EM segmentation challenge.
Fast Piecewise-Affine Motion Estimation Without Segmentation
Feb 06, 2018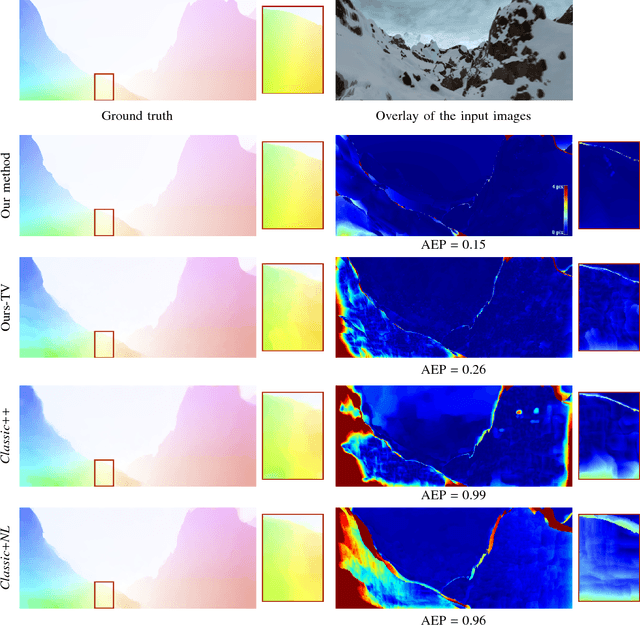



Abstract:Current algorithmic approaches for piecewise affine motion estimation are based on alternating motion segmentation and estimation. We propose a new method to estimate piecewise affine motion fields directly without intermediate segmentation. To this end, we reformulate the problem by imposing piecewise constancy of the parameter field, and derive a specific proximal splitting optimization scheme. A key component of our framework is an efficient one-dimensional piecewise-affine estimator for vector-valued signals. The first advantage of our approach over segmentation-based methods is its absence of initialization. The second advantage is its lower computational cost which is independent of the complexity of the motion field. In addition to these features, we demonstrate competitive accuracy with other piecewise-parametric methods on standard evaluation benchmarks. Our new regularization scheme also outperforms the more standard use of total variation and total generalized variation.
Model-based learning of local image features for unsupervised texture segmentation
Aug 01, 2017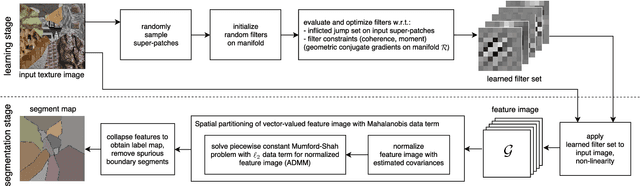


Abstract:Features that capture well the textural patterns of a certain class of images are crucial for the performance of texture segmentation methods. The manual selection of features or designing new ones can be a tedious task. Therefore, it is desirable to automatically adapt the features to a certain image or class of images. Typically, this requires a large set of training images with similar textures and ground truth segmentation. In this work, we propose a framework to learn features for texture segmentation when no such training data is available. The cost function for our learning process is constructed to match a commonly used segmentation model, the piecewise constant Mumford-Shah model. This means that the features are learned such that they provide an approximately piecewise constant feature image with a small jump set. Based on this idea, we develop a two-stage algorithm which first learns suitable convolutional features and then performs a segmentation. We note that the features can be learned from a small set of images, from a single image, or even from image patches. The proposed method achieves a competitive rank in the Prague texture segmentation benchmark, and it is effective for segmenting histological images.
Mumford-Shah and Potts Regularization for Manifold-Valued Data with Applications to DTI and Q-Ball Imaging
Oct 07, 2014
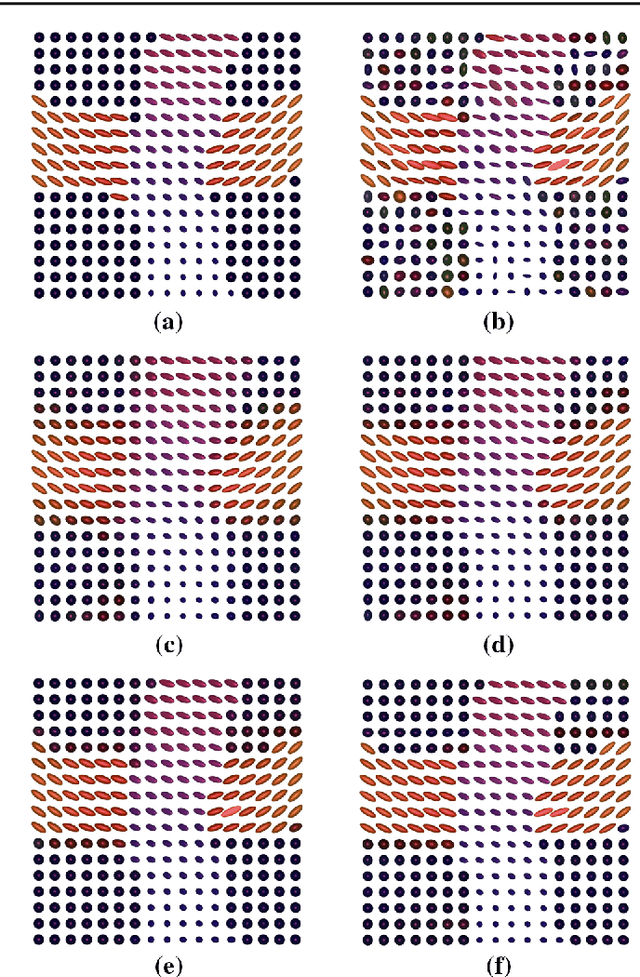
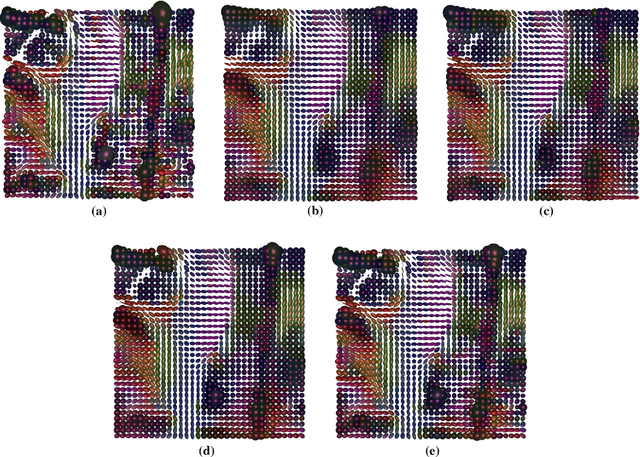
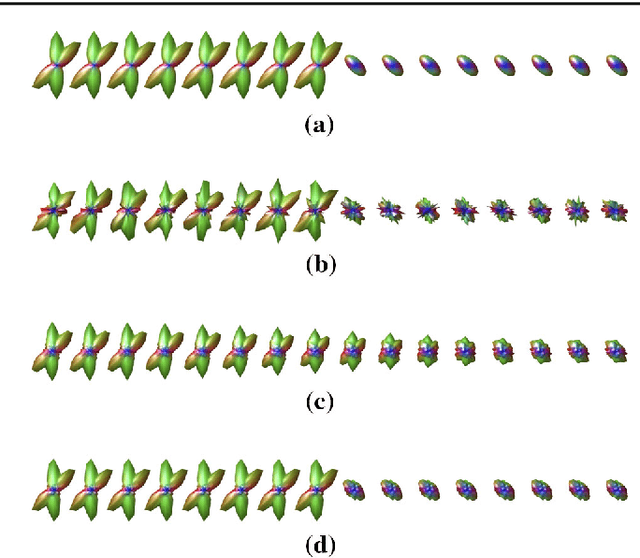
Abstract:Mumford-Shah and Potts functionals are powerful variational models for regularization which are widely used in signal and image processing; typical applications are edge-preserving denoising and segmentation. Being both non-smooth and non-convex, they are computationally challenging even for scalar data. For manifold-valued data, the problem becomes even more involved since typical features of vector spaces are not available. In this paper, we propose algorithms for Mumford-Shah and for Potts regularization of manifold-valued signals and images. For the univariate problems, we derive solvers based on dynamic programming combined with (convex) optimization techniques for manifold-valued data. For the class of Cartan-Hadamard manifolds (which includes the data space in diffusion tensor imaging), we show that our algorithms compute global minimizers for any starting point. For the multivariate Mumford-Shah and Potts problems (for image regularization) we propose a splitting into suitable subproblems which we can solve exactly using the techniques developed for the corresponding univariate problems. Our method does not require any a priori restrictions on the edge set and we do not have to discretize the data space. We apply our method to diffusion tensor imaging (DTI) as well as Q-ball imaging. Using the DTI model, we obtain a segmentation of the corpus callosum.
Total variation regularization for manifold-valued data
Dec 30, 2013



Abstract:We consider total variation minimization for manifold valued data. We propose a cyclic proximal point algorithm and a parallel proximal point algorithm to minimize TV functionals with $\ell^p$-type data terms in the manifold case. These algorithms are based on iterative geodesic averaging which makes them easily applicable to a large class of data manifolds. As an application, we consider denoising images which take their values in a manifold. We apply our algorithms to diffusion tensor images, interferometric SAR images as well as sphere and cylinder valued images. For the class of Cartan-Hadamard manifolds (which includes the data space in diffusion tensor imaging) we show the convergence of the proposed TV minimizing algorithms to a global minimizer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge