Model-based learning of local image features for unsupervised texture segmentation

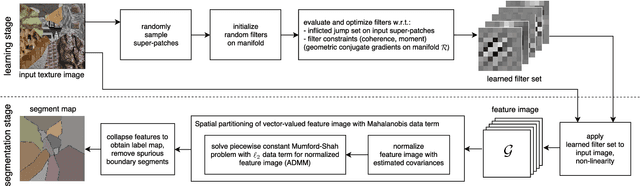
Features that capture well the textural patterns of a certain class of images are crucial for the performance of texture segmentation methods. The manual selection of features or designing new ones can be a tedious task. Therefore, it is desirable to automatically adapt the features to a certain image or class of images. Typically, this requires a large set of training images with similar textures and ground truth segmentation. In this work, we propose a framework to learn features for texture segmentation when no such training data is available. The cost function for our learning process is constructed to match a commonly used segmentation model, the piecewise constant Mumford-Shah model. This means that the features are learned such that they provide an approximately piecewise constant feature image with a small jump set. Based on this idea, we develop a two-stage algorithm which first learns suitable convolutional features and then performs a segmentation. We note that the features can be learned from a small set of images, from a single image, or even from image patches. The proposed method achieves a competitive rank in the Prague texture segmentation benchmark, and it is effective for segmenting histological images.

A Bimodal Co-Sparse Analysis Model for Image Processing

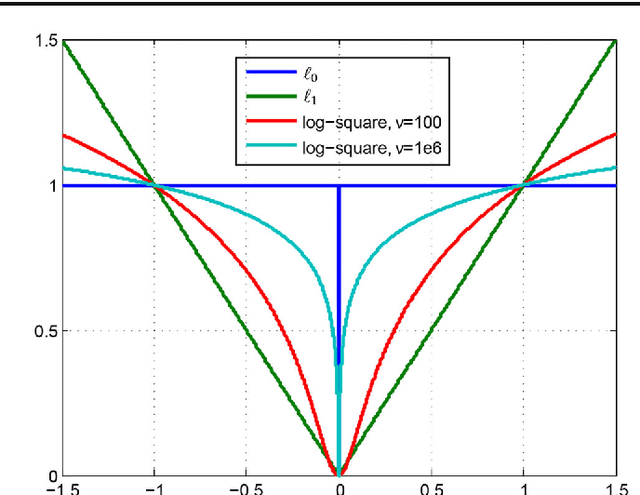
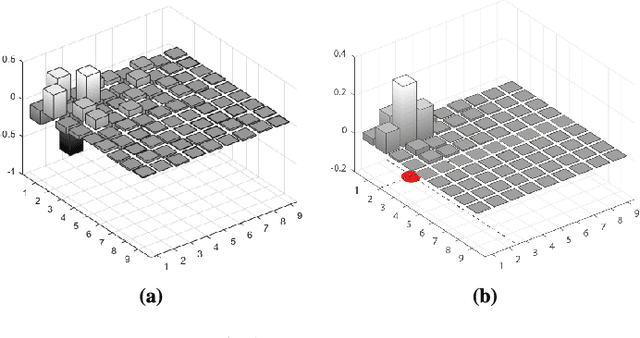
The success of many computer vision tasks lies in the ability to exploit the interdependency between different image modalities such as intensity and depth. Fusing corresponding information can be achieved on several levels, and one promising approach is the integration at a low level. Moreover, sparse signal models have successfully been used in many vision applications. Within this area of research, the so called co-sparse analysis model has attracted considerably less attention than its well-known counterpart, the sparse synthesis model, although it has been proven to be very useful in various image processing applications. In this paper, we propose a co-sparse analysis model that is able to capture the interdependency of two image modalities. It is based on the assumption that a pair of analysis operators exists, so that the co-supports of the corresponding bimodal image structures are correlated. We propose an algorithm that is able to learn such a coupled pair of operators from registered and noise-free training data. Furthermore, we explain how this model can be applied to solve linear inverse problems in image processing and how it can be used for image registration tasks. This paper extends the work of some of the authors by two major contributions. Firstly, a modification of the learning process is proposed that a priori guarantees unit norm and zero-mean of the rows of the operator. This accounts for the intuition that contrast in image modalities carries the most information. Secondly, the model is used in a novel bimodal image registration algorithm which estimates the transformation parameters of unregistered images of different modalities.

A Joint Intensity and Depth Co-Sparse Analysis Model for Depth Map Super-Resolution

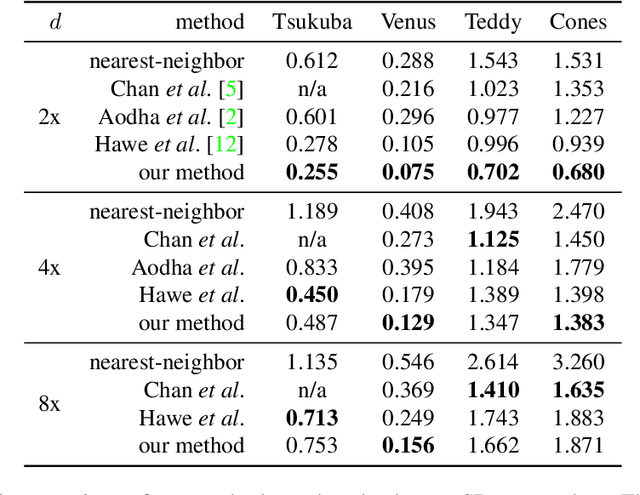
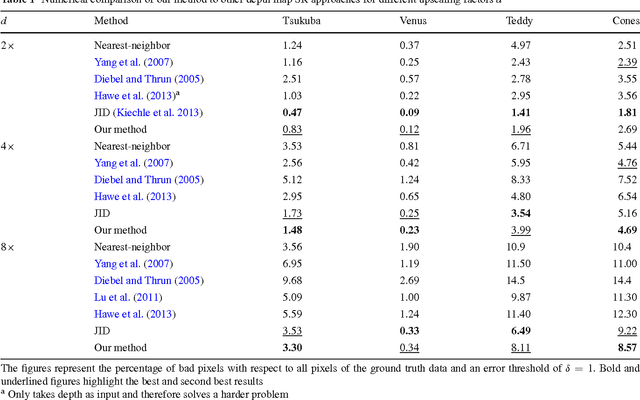
High-resolution depth maps can be inferred from low-resolution depth measurements and an additional high-resolution intensity image of the same scene. To that end, we introduce a bimodal co-sparse analysis model, which is able to capture the interdependency of registered intensity and depth information. This model is based on the assumption that the co-supports of corresponding bimodal image structures are aligned when computed by a suitable pair of analysis operators. No analytic form of such operators exist and we propose a method for learning them from a set of registered training signals. This learning process is done offline and returns a bimodal analysis operator that is universally applicable to natural scenes. We use this to exploit the bimodal co-sparse analysis model as a prior for solving inverse problems, which leads to an efficient algorithm for depth map super-resolution.