A Bimodal Co-Sparse Analysis Model for Image Processing

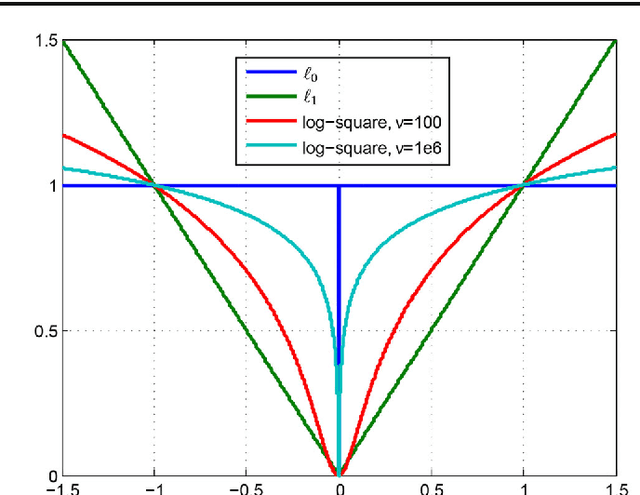
The success of many computer vision tasks lies in the ability to exploit the interdependency between different image modalities such as intensity and depth. Fusing corresponding information can be achieved on several levels, and one promising approach is the integration at a low level. Moreover, sparse signal models have successfully been used in many vision applications. Within this area of research, the so called co-sparse analysis model has attracted considerably less attention than its well-known counterpart, the sparse synthesis model, although it has been proven to be very useful in various image processing applications. In this paper, we propose a co-sparse analysis model that is able to capture the interdependency of two image modalities. It is based on the assumption that a pair of analysis operators exists, so that the co-supports of the corresponding bimodal image structures are correlated. We propose an algorithm that is able to learn such a coupled pair of operators from registered and noise-free training data. Furthermore, we explain how this model can be applied to solve linear inverse problems in image processing and how it can be used for image registration tasks. This paper extends the work of some of the authors by two major contributions. Firstly, a modification of the learning process is proposed that a priori guarantees unit norm and zero-mean of the rows of the operator. This accounts for the intuition that contrast in image modalities carries the most information. Secondly, the model is used in a novel bimodal image registration algorithm which estimates the transformation parameters of unregistered images of different modalities.

Co-Sparse Textural Similarity for Image Segmentation

We propose an algorithm for segmenting natural images based on texture and color information, which leverages the co-sparse analysis model for image segmentation within a convex multilabel optimization framework. As a key ingredient of this method, we introduce a novel textural similarity measure, which builds upon the co-sparse representation of image patches. We propose a Bayesian approach to merge textural similarity with information about color and location. Combined with recently developed convex multilabel optimization methods this leads to an efficient algorithm for both supervised and unsupervised segmentation, which is easily parallelized on graphics hardware. The approach provides competitive results in unsupervised segmentation and outperforms state-of-the-art interactive segmentation methods on the Graz Benchmark.

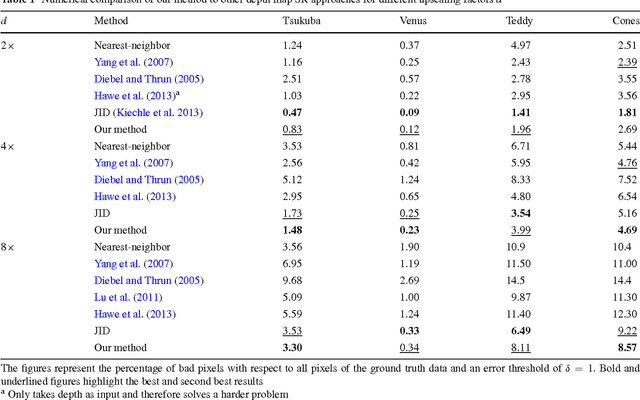
A Joint Intensity and Depth Co-Sparse Analysis Model for Depth Map Super-Resolution

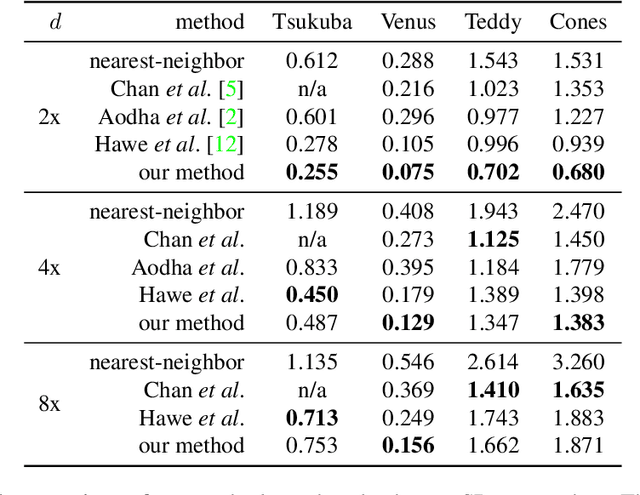
High-resolution depth maps can be inferred from low-resolution depth measurements and an additional high-resolution intensity image of the same scene. To that end, we introduce a bimodal co-sparse analysis model, which is able to capture the interdependency of registered intensity and depth information. This model is based on the assumption that the co-supports of corresponding bimodal image structures are aligned when computed by a suitable pair of analysis operators. No analytic form of such operators exist and we propose a method for learning them from a set of registered training signals. This learning process is done offline and returns a bimodal analysis operator that is universally applicable to natural scenes. We use this to exploit the bimodal co-sparse analysis model as a prior for solving inverse problems, which leads to an efficient algorithm for depth map super-resolution.

Analysis Operator Learning and Its Application to Image Reconstruction

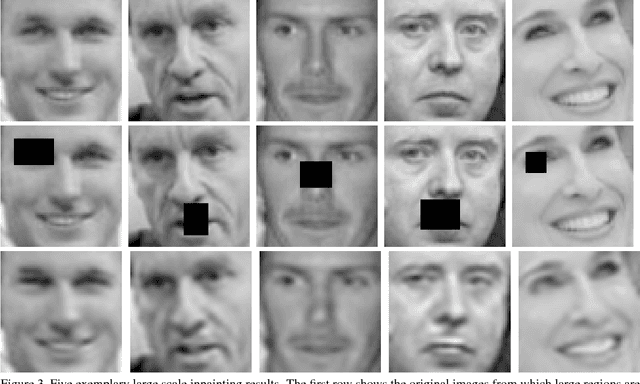
Exploiting a priori known structural information lies at the core of many image reconstruction methods that can be stated as inverse problems. The synthesis model, which assumes that images can be decomposed into a linear combination of very few atoms of some dictionary, is now a well established tool for the design of image reconstruction algorithms. An interesting alternative is the analysis model, where the signal is multiplied by an analysis operator and the outcome is assumed to be the sparse. This approach has only recently gained increasing interest. The quality of reconstruction methods based on an analysis model severely depends on the right choice of the suitable operator. In this work, we present an algorithm for learning an analysis operator from training images. Our method is based on an $\ell_p$-norm minimization on the set of full rank matrices with normalized columns. We carefully introduce the employed conjugate gradient method on manifolds, and explain the underlying geometry of the constraints. Moreover, we compare our approach to state-of-the-art methods for image denoising, inpainting, and single image super-resolution. Our numerical results show competitive performance of our general approach in all presented applications compared to the specialized state-of-the-art techniques.

Separable Dictionary Learning

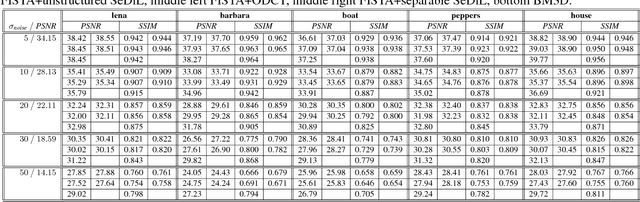
Many techniques in computer vision, machine learning, and statistics rely on the fact that a signal of interest admits a sparse representation over some dictionary. Dictionaries are either available analytically, or can be learned from a suitable training set. While analytic dictionaries permit to capture the global structure of a signal and allow a fast implementation, learned dictionaries often perform better in applications as they are more adapted to the considered class of signals. In imagery, unfortunately, the numerical burden for (i) learning a dictionary and for (ii) employing the dictionary for reconstruction tasks only allows to deal with relatively small image patches that only capture local image information. The approach presented in this paper aims at overcoming these drawbacks by allowing a separable structure on the dictionary throughout the learning process. On the one hand, this permits larger patch-sizes for the learning phase, on the other hand, the dictionary is applied efficiently in reconstruction tasks. The learning procedure is based on optimizing over a product of spheres which updates the dictionary as a whole, thus enforces basic dictionary properties such as mutual coherence explicitly during the learning procedure. In the special case where no separable structure is enforced, our method competes with state-of-the-art dictionary learning methods like K-SVD.