Learning Co-Sparse Analysis Operators with Separable Structures

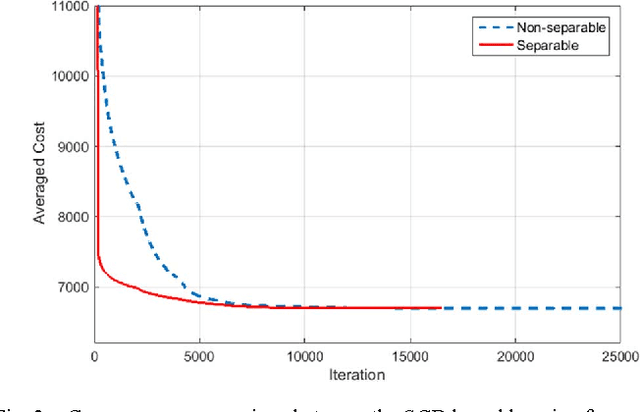
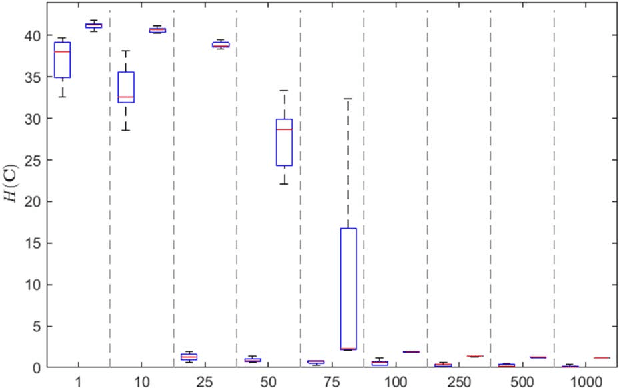
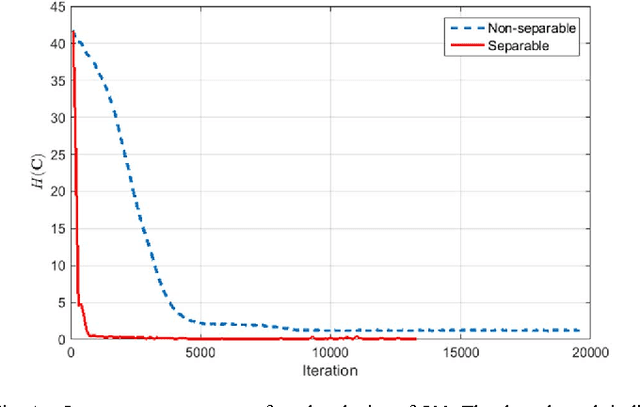
In the co-sparse analysis model a set of filters is applied to a signal out of the signal class of interest yielding sparse filter responses. As such, it may serve as a prior in inverse problems, or for structural analysis of signals that are known to belong to the signal class. The more the model is adapted to the class, the more reliable it is for these purposes. The task of learning such operators for a given class is therefore a crucial problem. In many applications, it is also required that the filter responses are obtained in a timely manner, which can be achieved by filters with a separable structure. Not only can operators of this sort be efficiently used for computing the filter responses, but they also have the advantage that less training samples are required to obtain a reliable estimate of the operator. The first contribution of this work is to give theoretical evidence for this claim by providing an upper bound for the sample complexity of the learning process. The second is a stochastic gradient descent (SGD) method designed to learn an analysis operator with separable structures, which includes a novel and efficient step size selection rule. Numerical experiments are provided that link the sample complexity to the convergence speed of the SGD algorithm.

Sample Complexity of Dictionary Learning and other Matrix Factorizations

Many modern tools in machine learning and signal processing, such as sparse dictionary learning, principal component analysis (PCA), non-negative matrix factorization (NMF), $K$-means clustering, etc., rely on the factorization of a matrix obtained by concatenating high-dimensional vectors from a training collection. While the idealized task would be to optimize the expected quality of the factors over the underlying distribution of training vectors, it is achieved in practice by minimizing an empirical average over the considered collection. The focus of this paper is to provide sample complexity estimates to uniformly control how much the empirical average deviates from the expected cost function. Standard arguments imply that the performance of the empirical predictor also exhibit such guarantees. The level of genericity of the approach encompasses several possible constraints on the factors (tensor product structure, shift-invariance, sparsity \ldots), thus providing a unified perspective on the sample complexity of several widely used matrix factorization schemes. The derived generalization bounds behave proportional to $\sqrt{\log(n)/n}$ w.r.t.\ the number of samples $n$ for the considered matrix factorization techniques.

Separable Cosparse Analysis Operator Learning

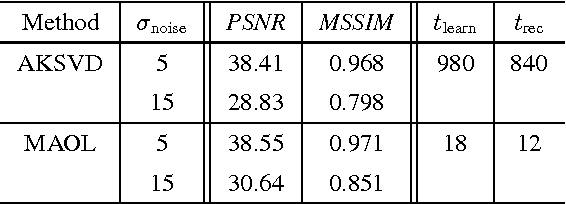
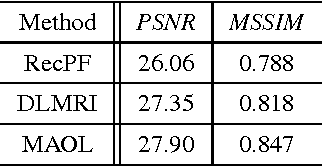
The ability of having a sparse representation for a certain class of signals has many applications in data analysis, image processing, and other research fields. Among sparse representations, the cosparse analysis model has recently gained increasing interest. Many signals exhibit a multidimensional structure, e.g. images or three-dimensional MRI scans. Most data analysis and learning algorithms use vectorized signals and thereby do not account for this underlying structure. The drawback of not taking the inherent structure into account is a dramatic increase in computational cost. We propose an algorithm for learning a cosparse Analysis Operator that adheres to the preexisting structure of the data, and thus allows for a very efficient implementation. This is achieved by enforcing a separable structure on the learned operator. Our learning algorithm is able to deal with multidimensional data of arbitrary order. We evaluate our method on volumetric data at the example of three-dimensional MRI scans.

On The Sample Complexity of Sparse Dictionary Learning

In the synthesis model signals are represented as a sparse combinations of atoms from a dictionary. Dictionary learning describes the acquisition process of the underlying dictionary for a given set of training samples. While ideally this would be achieved by optimizing the expectation of the factors over the underlying distribution of the training data, in practice the necessary information about the distribution is not available. Therefore, in real world applications it is achieved by minimizing an empirical average over the available samples. The main goal of this paper is to provide a sample complexity estimate that controls to what extent the empirical average deviates from the cost function. This estimate then provides a suitable estimate to the accuracy of the representation of the learned dictionary. The presented approach exemplifies the general results proposed by the authors in Sample Complexity of Dictionary Learning and other Matrix Factorizations, Gribonval et al. and gives more concrete bounds of the sample complexity of dictionary learning. We cover a variety of sparsity measures employed in the learning procedure.

Separable Dictionary Learning

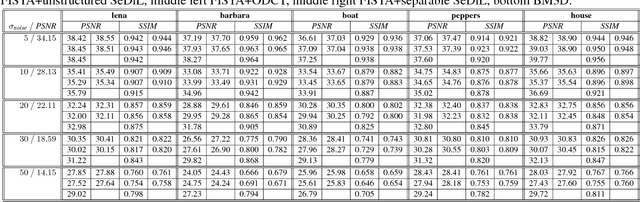
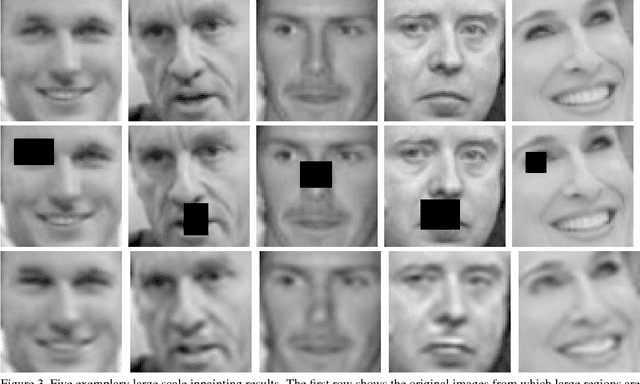
Many techniques in computer vision, machine learning, and statistics rely on the fact that a signal of interest admits a sparse representation over some dictionary. Dictionaries are either available analytically, or can be learned from a suitable training set. While analytic dictionaries permit to capture the global structure of a signal and allow a fast implementation, learned dictionaries often perform better in applications as they are more adapted to the considered class of signals. In imagery, unfortunately, the numerical burden for (i) learning a dictionary and for (ii) employing the dictionary for reconstruction tasks only allows to deal with relatively small image patches that only capture local image information. The approach presented in this paper aims at overcoming these drawbacks by allowing a separable structure on the dictionary throughout the learning process. On the one hand, this permits larger patch-sizes for the learning phase, on the other hand, the dictionary is applied efficiently in reconstruction tasks. The learning procedure is based on optimizing over a product of spheres which updates the dictionary as a whole, thus enforces basic dictionary properties such as mutual coherence explicitly during the learning procedure. In the special case where no separable structure is enforced, our method competes with state-of-the-art dictionary learning methods like K-SVD.