Separable Cosparse Analysis Operator Learning
Paper and Code
Jun 06, 2014
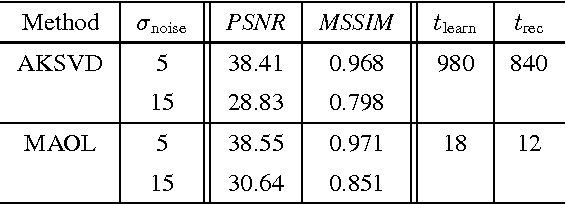
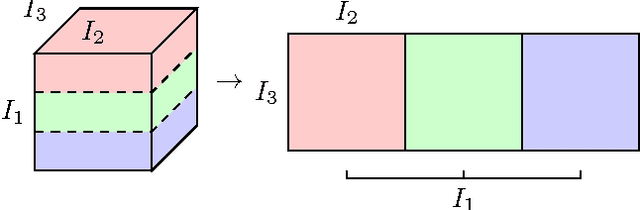
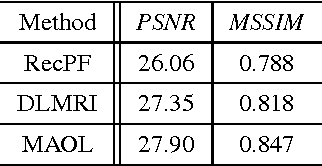
The ability of having a sparse representation for a certain class of signals has many applications in data analysis, image processing, and other research fields. Among sparse representations, the cosparse analysis model has recently gained increasing interest. Many signals exhibit a multidimensional structure, e.g. images or three-dimensional MRI scans. Most data analysis and learning algorithms use vectorized signals and thereby do not account for this underlying structure. The drawback of not taking the inherent structure into account is a dramatic increase in computational cost. We propose an algorithm for learning a cosparse Analysis Operator that adheres to the preexisting structure of the data, and thus allows for a very efficient implementation. This is achieved by enforcing a separable structure on the learned operator. Our learning algorithm is able to deal with multidimensional data of arbitrary order. We evaluate our method on volumetric data at the example of three-dimensional MRI scans.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge