Multi-level Geometric Optimization for Regularised Constrained Linear Inverse Problems

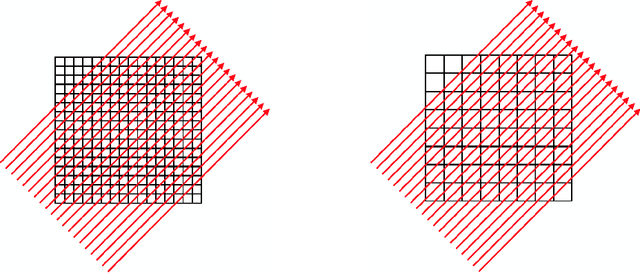
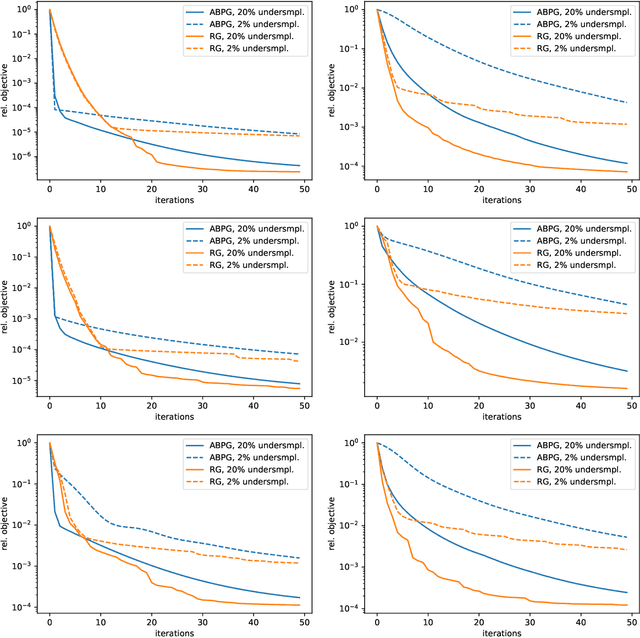
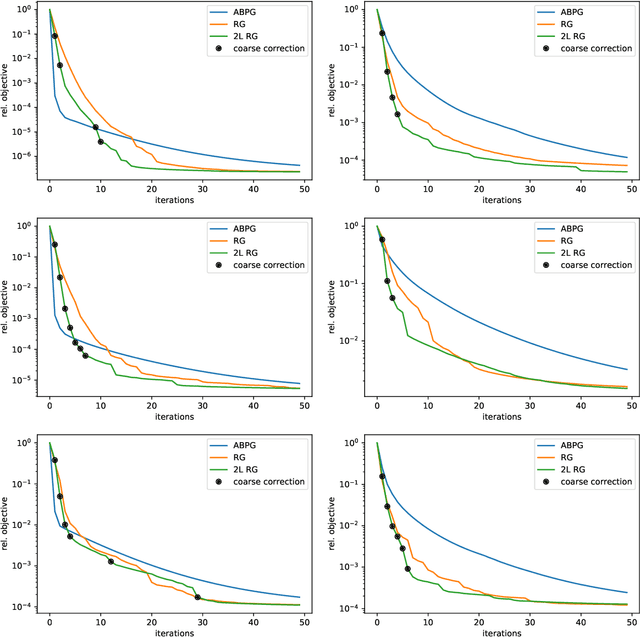
We present a geometric multi-level optimization approach that smoothly incorporates box constraints. Given a box constrained optimization problem, we consider a hierarchy of models with varying discretization levels. Finer models are accurate but expensive to compute, while coarser models are less accurate but cheaper to compute. When working at the fine level, multi-level optimisation computes the search direction based on a coarser model which speeds up updates at the fine level. Moreover, exploiting geometry induced by the hierarchy the feasibility of the updates is preserved. In particular, our approach extends classical components of multigrid methods like restriction and prolongation to the Riemannian structure of our constraints.

Self-Assignment Flows for Unsupervised Data Labeling on Graphs

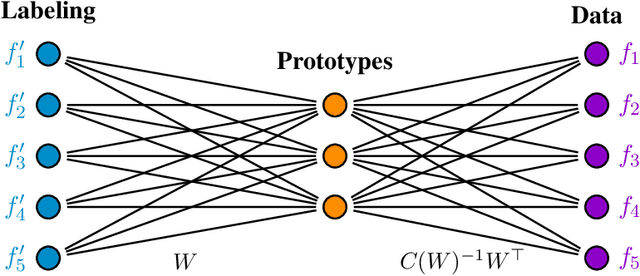
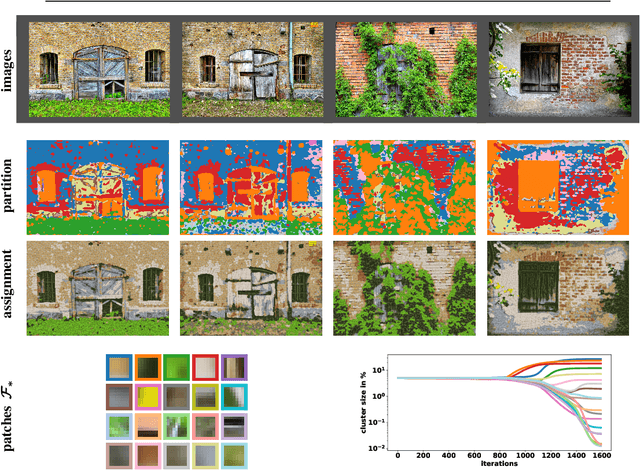
This paper extends the recently introduced assignment flow approach for supervised image labeling to unsupervised scenarios where no labels are given. The resulting self-assignment flow takes a pairwise data affinity matrix as input data and maximizes the correlation with a low-rank matrix that is parametrized by the variables of the assignment flow, which entails an assignment of the data to themselves through the formation of latent labels (feature prototypes). A single user parameter, the neighborhood size for the geometric regularization of assignments, drives the entire process. By smooth geodesic interpolation between different normalizations of self-assignment matrices on the positive definite matrix manifold, a one-parameter family of self-assignment flows is defined. Accordingly, our approach can be characterized from different viewpoints, e.g. as performing spatially regularized, rank-constrained discrete optimal transport, or as computing spatially regularized normalized spectral cuts. Regarding combinatorial optimization, our approach successfully determines completely positive factorizations of self-assignments in large-scale scenarios, subject to spatial regularization. Various experiments including the unsupervised learning of patch dictionaries using a locally invariant distance function, illustrate the properties of the approach.

Unsupervised Assignment Flow: Label Learning on Feature Manifolds by Spatially Regularized Geometric Assignment

This paper introduces the unsupervised assignment flow that couples the assignment flow for supervised image labeling with Riemannian gradient flows for label evolution on feature manifolds. The latter component of the approach encompasses extensions of state-of-the-art clustering approaches to manifold-valued data. Coupling label evolution with the spatially regularized assignment flow induces a sparsifying effect that enables to learn compact label dictionaries in an unsupervised manner. Our approach alleviates the requirement for supervised labeling to have proper labels at hand, because an initial set of labels can evolve and adapt to better values while being assigned to given data. The separation between feature and assignment manifolds enables the flexible application which is demonstrated for three scenarios with manifold-valued features. Experiments demonstrate beneficial effect in both directions: adaptivity of labels improves image labeling, and steering label evolution by spatially regularized assignments leads to proper labels, because the assignment flow for supervised labeling is exactly used without any approximation for label learning.