Self-Assignment Flows for Unsupervised Data Labeling on Graphs
Paper and Code
Nov 08, 2019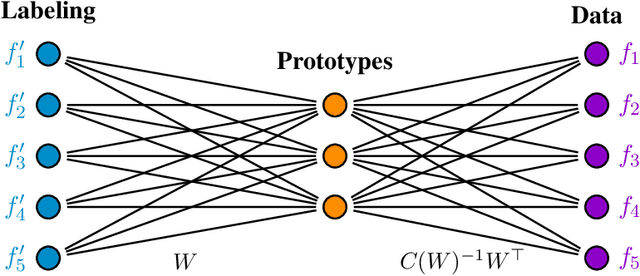

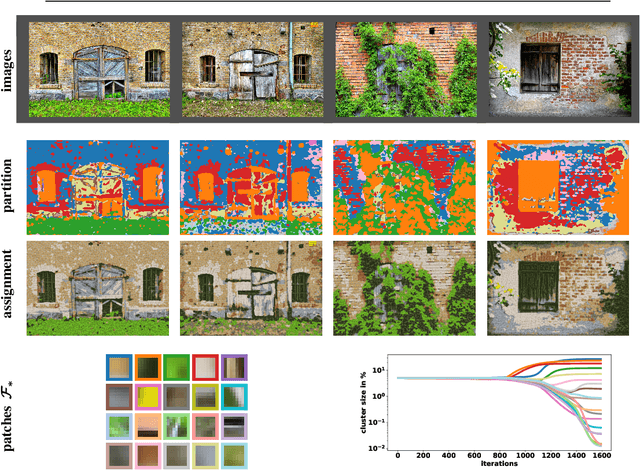

This paper extends the recently introduced assignment flow approach for supervised image labeling to unsupervised scenarios where no labels are given. The resulting self-assignment flow takes a pairwise data affinity matrix as input data and maximizes the correlation with a low-rank matrix that is parametrized by the variables of the assignment flow, which entails an assignment of the data to themselves through the formation of latent labels (feature prototypes). A single user parameter, the neighborhood size for the geometric regularization of assignments, drives the entire process. By smooth geodesic interpolation between different normalizations of self-assignment matrices on the positive definite matrix manifold, a one-parameter family of self-assignment flows is defined. Accordingly, our approach can be characterized from different viewpoints, e.g. as performing spatially regularized, rank-constrained discrete optimal transport, or as computing spatially regularized normalized spectral cuts. Regarding combinatorial optimization, our approach successfully determines completely positive factorizations of self-assignments in large-scale scenarios, subject to spatial regularization. Various experiments including the unsupervised learning of patch dictionaries using a locally invariant distance function, illustrate the properties of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge