Self-Certifying Classification by Linearized Deep Assignment

We propose a novel class of deep stochastic predictors for classifying metric data on graphs within the PAC-Bayes risk certification paradigm. Classifiers are realized as linearly parametrized deep assignment flows with random initial conditions. Building on the recent PAC-Bayes literature and data-dependent priors, this approach enables (i) to use risk bounds as training objectives for learning posterior distributions on the hypothesis space and (ii) to compute tight out-of-sample risk certificates of randomized classifiers more efficiently than related work. Comparison with empirical test set errors illustrates the performance and practicality of this self-certifying classification method.

Learning Linearized Assignment Flows for Image Labeling

We introduce a novel algorithm for estimating optimal parameters of linearized assignment flows for image labeling. An exact formula is derived for the parameter gradient of any loss function that is constrained by the linear system of ODEs determining the linearized assignment flow. We show how to efficiently evaluate this formula using a Krylov subspace and a low-rank approximation. This enables us to perform parameter learning by Riemannian gradient descent in the parameter space, without the need to backpropagate errors or to solve an adjoint equation, in less than 10 seconds for a $512\times 512$ image using just about $0.5$ GB memory. Experiments demonstrate that our method performs as good as highly-tuned machine learning software using automatic differentiation. Unlike methods employing automatic differentiation, our approach yields a low-dimensional representation of internal parameters and their dynamics which helps to understand how networks work and perform that realize assignment flows and generalizations thereof.

Assignment Flows for Data Labeling on Graphs: Convergence and Stability

The assignment flow recently introduced in the J. Math. Imaging and Vision 58/2 (2017), constitutes a high-dimensional dynamical system that evolves on an elementary statistical manifold and performs contextual labeling (classification) of data given in any metric space. Vertices of a given graph index the data points and define a system of neighborhoods. These neighborhoods together with nonnegative weight parameters define regularization of the evolution of label assignments to data points, through geometric averaging induced by the affine e-connection of information geometry. Regarding evolutionary game dynamics, the assignment flow may be characterized as a large system of replicator equations that are coupled by geometric averaging. This paper establishes conditions on the weight parameters that guarantee convergence of the continuous-time assignment flow to integral assignments (labelings), up to a negligible subset of situations that will not be encountered when working with real data in practice. Furthermore, we classify attractors of the flow and quantify corresponding basins of attraction. This provides convergence guarantees for the assignment flow which are extended to the discrete-time assignment flow that results from applying a Runge-Kutta-Munthe-Kaas scheme for numerical geometric integration of the assignment flow. Several counter-examples illustrate that violating the conditions may entail unfavorable behavior of the assignment flow regarding contextual data classification.

End-to-End Learned Random Walker for Seeded Image Segmentation

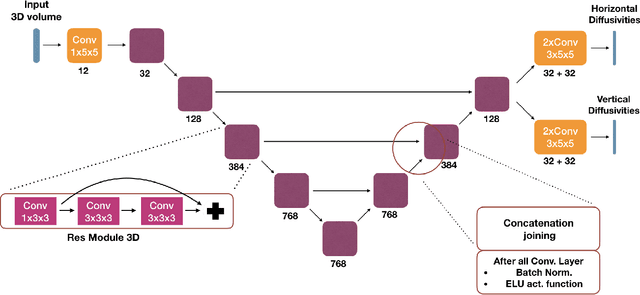
We present an end-to-end learned algorithm for seeded segmentation. Our method is based on the Random Walker algorithm, where we predict the edge weights of the underlying graph using a convolutional neural network. This can be interpreted as learning context-dependent diffusivities for a linear diffusion process. Besides calculating the exact gradient for optimizing these diffusivities, we also propose simplifications that sparsely sample the gradient and still yield competitive results. The proposed method achieves the currently best results on a seeded version of the CREMI neuron segmentation challenge.