Joint Metric Space Embedding by Unbalanced OT with Gromov-Wasserstein Marginal Penalization

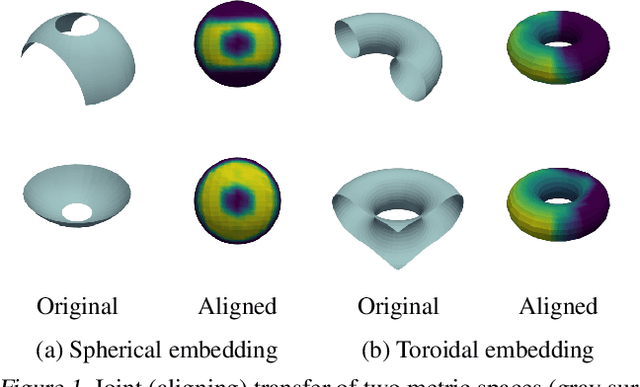
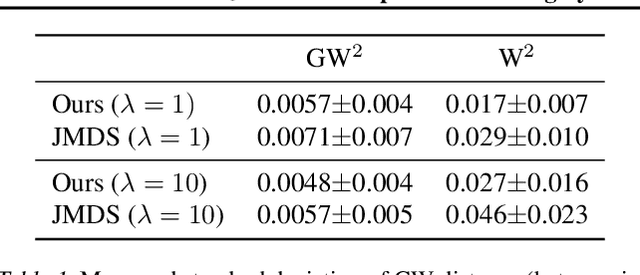
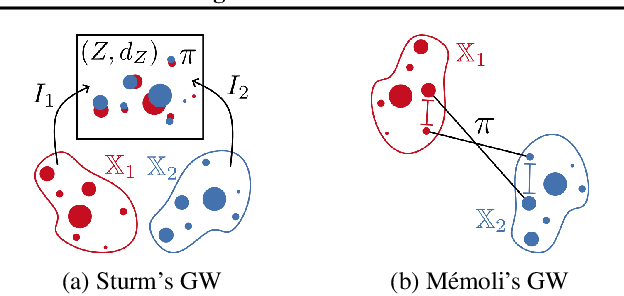
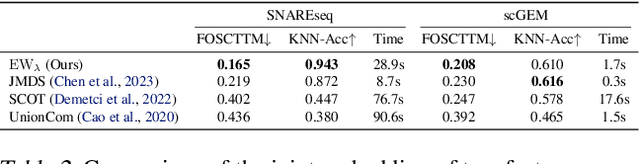
We propose a new approach for unsupervised alignment of heterogeneous datasets, which maps data from two different domains without any known correspondences to a common metric space. Our method is based on an unbalanced optimal transport problem with Gromov-Wasserstein marginal penalization. It can be seen as a counterpart to the recently introduced joint multidimensional scaling method. We prove that there exists a minimizer of our functional and that for penalization parameters going to infinity, the corresponding sequence of minimizers converges to a minimizer of the so-called embedded Wasserstein distance. Our model can be reformulated as a quadratic, multi-marginal, unbalanced optimal transport problem, for which a bi-convex relaxation admits a numerical solver via block-coordinate descent. We provide numerical examples for joint embeddings in Euclidean as well as non-Euclidean spaces.

Transfer Operators from Batches of Unpaired Points via Entropic Transport Kernels

In this paper, we are concerned with estimating the joint probability of random variables $X$ and $Y$, given $N$ independent observation blocks $(\boldsymbol{x}^i,\boldsymbol{y}^i)$, $i=1,\ldots,N$, each of $M$ samples $(\boldsymbol{x}^i,\boldsymbol{y}^i) = \bigl((x^i_j, y^i_{\sigma^i(j)}) \bigr)_{j=1}^M$, where $\sigma^i$ denotes an unknown permutation of i.i.d. sampled pairs $(x^i_j,y_j^i)$, $j=1,\ldots,M$. This means that the internal ordering of the $M$ samples within an observation block is not known. We derive a maximum-likelihood inference functional, propose a computationally tractable approximation and analyze their properties. In particular, we prove a $\Gamma$-convergence result showing that we can recover the true density from empirical approximations as the number $N$ of blocks goes to infinity. Using entropic optimal transport kernels, we model a class of hypothesis spaces of density functions over which the inference functional can be minimized. This hypothesis class is particularly suited for approximate inference of transfer operators from data. We solve the resulting discrete minimization problem by a modification of the EMML algorithm to take addional transition probability constraints into account and prove the convergence of this algorithm. Proof-of-concept examples demonstrate the potential of our method.