Freddie Åström
Image Labeling Based on Graphical Models Using Wasserstein Messages and Geometric Assignment
Jan 09, 2018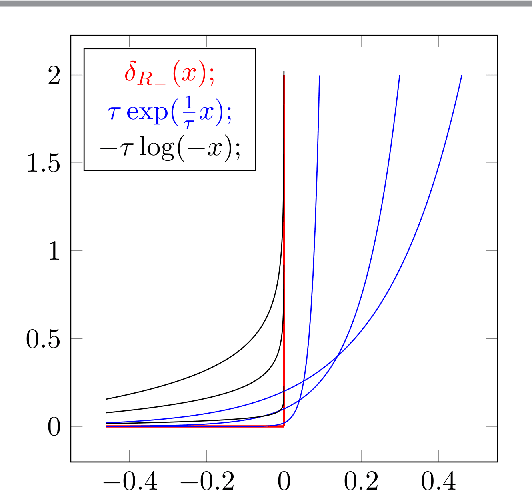
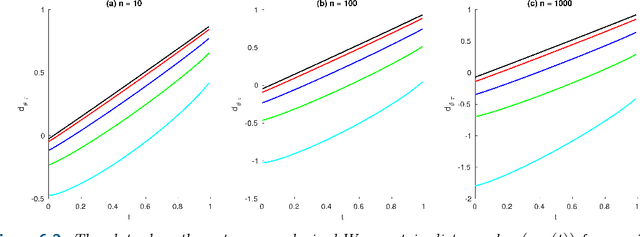
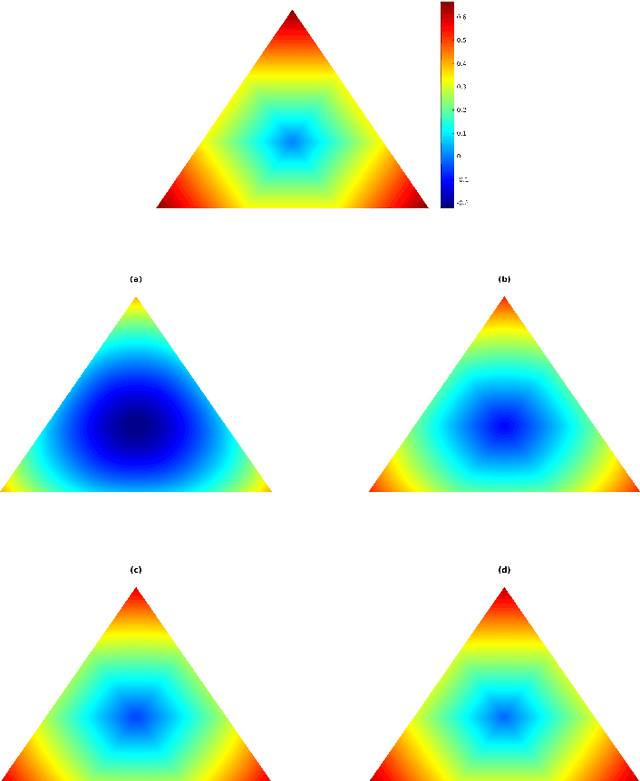
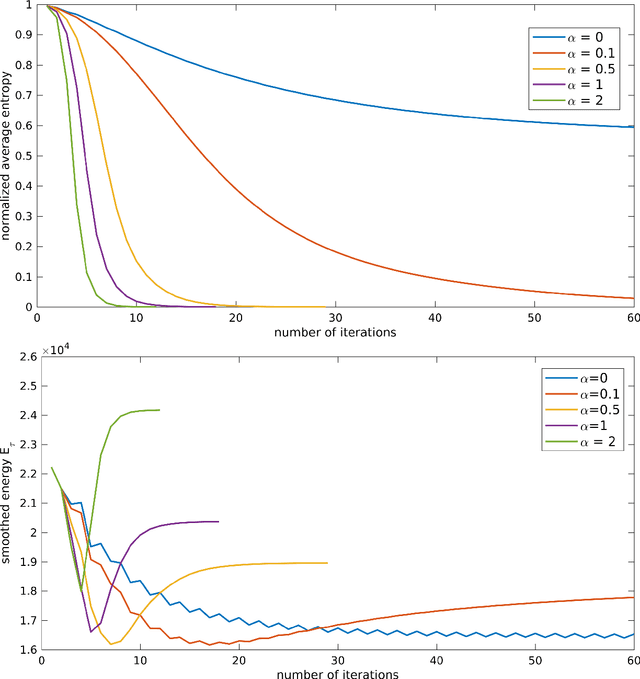
Abstract:We introduce a novel approach to Maximum A Posteriori inference based on discrete graphical models. By utilizing local Wasserstein distances for coupling assignment measures across edges of the underlying graph, a given discrete objective function is smoothly approximated and restricted to the assignment manifold. A corresponding multiplicative update scheme combines in a single process (i) geometric integration of the resulting Riemannian gradient flow and (ii) rounding to integral solutions that represent valid labelings. Throughout this process, local marginalization constraints known from the established LP relaxation are satisfied, whereas the smooth geometric setting results in rapidly converging iterations that can be carried out in parallel for every edge.
A Geometric Approach to Color Image Regularization
May 19, 2016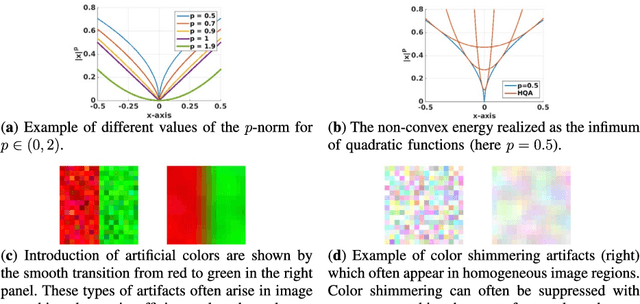
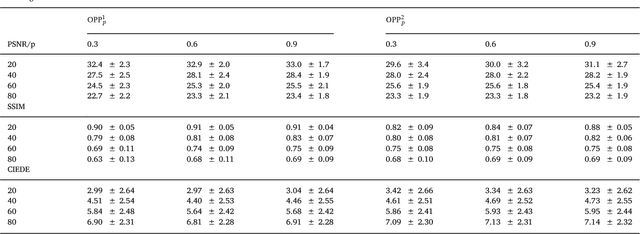
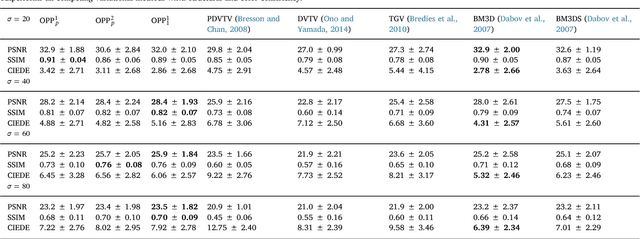
Abstract:We present a new vectorial total variation method that addresses the problem of color consistent image filtering. Our approach is inspired from the double-opponent cell representation in the human visual cortex. Existing methods of vectorial total variation regularizers have insufficient (or no) coupling between the color channels and thus may introduce color artifacts. We address this problem by introducing a novel coupling between the color channels related to a pullback-metric from the opponent space to the data (RGB color) space. Our energy is a non-convex, non-smooth higher-order vectorial total variation approach and promotes color consistent image filtering via a coupling term. For a convex variant, we show well-posedness and existence of a solution in the space of vectorial bounded variation. For the higher-order scheme we employ a half-quadratic strategy, which model the non-convex energy terms as the infimum of a sequence of quadratic functions. In experiments, we elaborate on traditional image restoration applications of inpainting, deblurring and denoising. Regarding the latter, we demonstrate state of the art restoration quality with respect to structure coherence and color consistency.
Image Labeling by Assignment
Mar 16, 2016


Abstract:We introduce a novel geometric approach to the image labeling problem. Abstracting from specific labeling applications, a general objective function is defined on a manifold of stochastic matrices, whose elements assign prior data that are given in any metric space, to observed image measurements. The corresponding Riemannian gradient flow entails a set of replicator equations, one for each data point, that are spatially coupled by geometric averaging on the manifold. Starting from uniform assignments at the barycenter as natural initialization, the flow terminates at some global maximum, each of which corresponds to an image labeling that uniquely assigns the prior data. Our geometric variational approach constitutes a smooth non-convex inner approximation of the general image labeling problem, implemented with sparse interior-point numerics in terms of parallel multiplicative updates that converge efficiently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge