Efficient Trajectory Inference in Wasserstein Space Using Consecutive Averaging

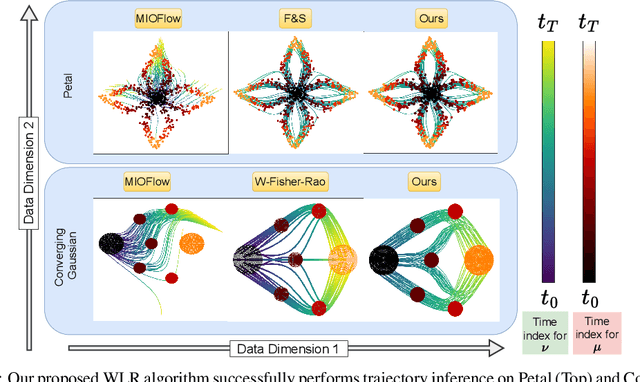
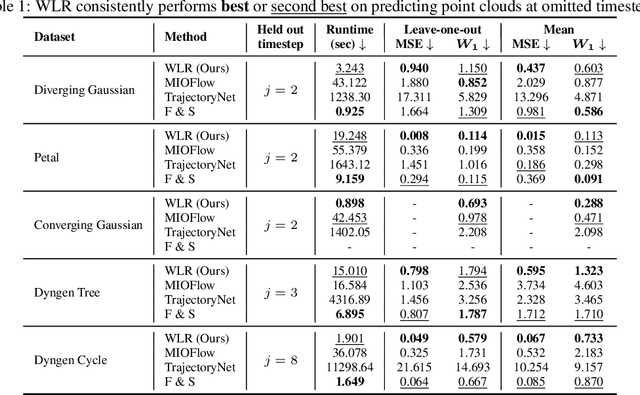
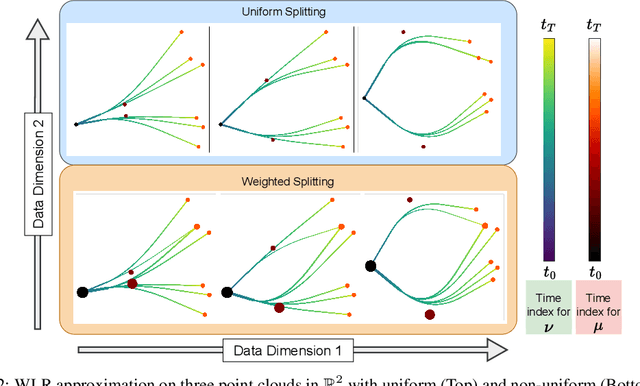
Capturing data from dynamic processes through cross-sectional measurements is seen in many fields such as computational biology. Trajectory inference deals with the challenge of reconstructing continuous processes from such observations. In this work, we propose methods for B-spline approximation and interpolation of point clouds through consecutive averaging that is instrinsic to the Wasserstein space. Combining subdivision schemes with optimal transport-based geodesic, our methods carry out trajectory inference at a chosen level of precision and smoothness, and can automatically handle scenarios where particles undergo division over time. We rigorously evaluate our method by providing convergence guarantees and testing it on simulated cell data characterized by bifurcations and merges, comparing its performance against state-of-the-art trajectory inference and interpolation methods. The results not only underscore the effectiveness of our method in inferring trajectories, but also highlight the benefit of performing interpolation and approximation that respect the inherent geometric properties of the data.

Point Cloud Classification via Deep Set Linearized Optimal Transport

We introduce Deep Set Linearized Optimal Transport, an algorithm designed for the efficient simultaneous embedding of point clouds into an $L^2-$space. This embedding preserves specific low-dimensional structures within the Wasserstein space while constructing a classifier to distinguish between various classes of point clouds. Our approach is motivated by the observation that $L^2-$distances between optimal transport maps for distinct point clouds, originating from a shared fixed reference distribution, provide an approximation of the Wasserstein-2 distance between these point clouds, under certain assumptions. To learn approximations of these transport maps, we employ input convex neural networks (ICNNs) and establish that, under specific conditions, Euclidean distances between samples from these ICNNs closely mirror Wasserstein-2 distances between the true distributions. Additionally, we train a discriminator network that attaches weights these samples and creates a permutation invariant classifier to differentiate between different classes of point clouds. We showcase the advantages of our algorithm over the standard deep set approach through experiments on a flow cytometry dataset with a limited number of labeled point clouds.

Manifold learning in Wasserstein space

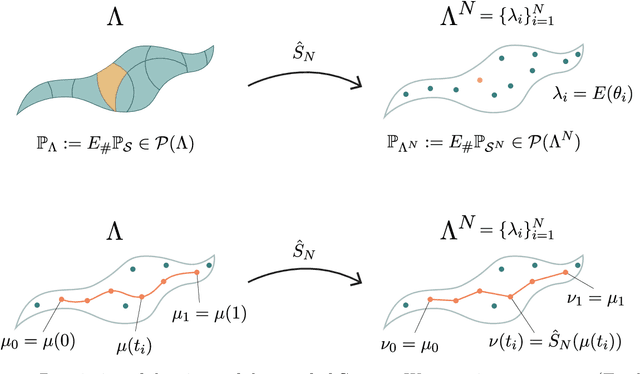
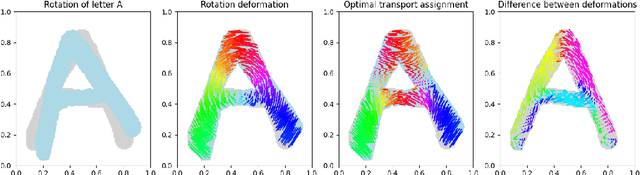
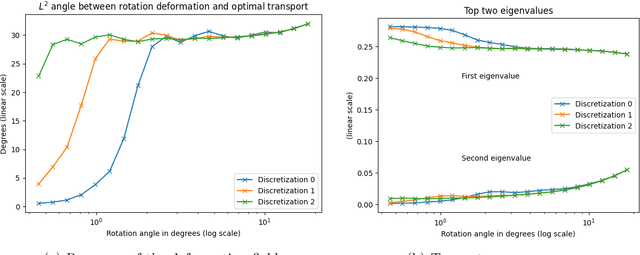
This paper aims at building the theoretical foundations for manifold learning algorithms in the space of absolutely continuous probability measures on a compact and convex subset of $\mathbb{R}^d$, metrized with the Wasserstein-2 distance $W$. We begin by introducing a natural construction of submanifolds $\Lambda$ of probability measures equipped with metric $W_\Lambda$, the geodesic restriction of $W$ to $\Lambda$. In contrast to other constructions, these submanifolds are not necessarily flat, but still allow for local linearizations in a similar fashion to Riemannian submanifolds of $\mathbb{R}^d$. We then show how the latent manifold structure of $(\Lambda,W_{\Lambda})$ can be learned from samples $\{\lambda_i\}_{i=1}^N$ of $\Lambda$ and pairwise extrinsic Wasserstein distances $W$ only. In particular, we show that the metric space $(\Lambda,W_{\Lambda})$ can be asymptotically recovered in the sense of Gromov--Wasserstein from a graph with nodes $\{\lambda_i\}_{i=1}^N$ and edge weights $W(\lambda_i,\lambda_j)$. In addition, we demonstrate how the tangent space at a sample $\lambda$ can be asymptotically recovered via spectral analysis of a suitable "covariance operator" using optimal transport maps from $\lambda$ to sufficiently close and diverse samples $\{\lambda_i\}_{i=1}^N$. The paper closes with some explicit constructions of submanifolds $\Lambda$ and numerical examples on the recovery of tangent spaces through spectral analysis.

Linearized Wasserstein dimensionality reduction with approximation guarantees

We introduce LOT Wassmap, a computationally feasible algorithm to uncover low-dimensional structures in the Wasserstein space. The algorithm is motivated by the observation that many datasets are naturally interpreted as probability measures rather than points in $\mathbb{R}^n$, and that finding low-dimensional descriptions of such datasets requires manifold learning algorithms in the Wasserstein space. Most available algorithms are based on computing the pairwise Wasserstein distance matrix, which can be computationally challenging for large datasets in high dimensions. Our algorithm leverages approximation schemes such as Sinkhorn distances and linearized optimal transport to speed-up computations, and in particular, avoids computing a pairwise distance matrix. We provide guarantees on the embedding quality under such approximations, including when explicit descriptions of the probability measures are not available and one must deal with finite samples instead. Experiments demonstrate that LOT Wassmap attains correct embeddings and that the quality improves with increased sample size. We also show how LOT Wassmap significantly reduces the computational cost when compared to algorithms that depend on pairwise distance computations.

Supervised learning of sheared distributions using linearized optimal transport

In this paper we study supervised learning tasks on the space of probability measures. We approach this problem by embedding the space of probability measures into $L^2$ spaces using the optimal transport framework. In the embedding spaces, regular machine learning techniques are used to achieve linear separability. This idea has proved successful in applications and when the classes to be separated are generated by shifts and scalings of a fixed measure. This paper extends the class of elementary transformations suitable for the framework to families of shearings, describing conditions under which two classes of sheared distributions can be linearly separated. We furthermore give necessary bounds on the transformations to achieve a pre-specified separation level, and show how multiple embeddings can be used to allow for larger families of transformations. We demonstrate our results on image classification tasks.

Linear Optimal Transport Embedding: Provable fast Wasserstein distance computation and classification for nonlinear problems

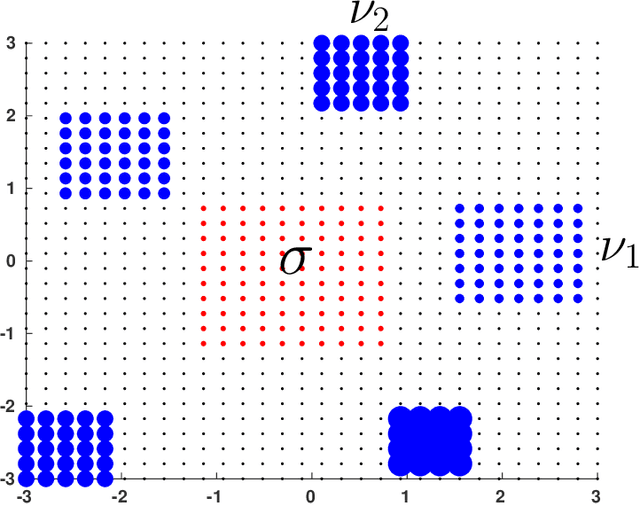
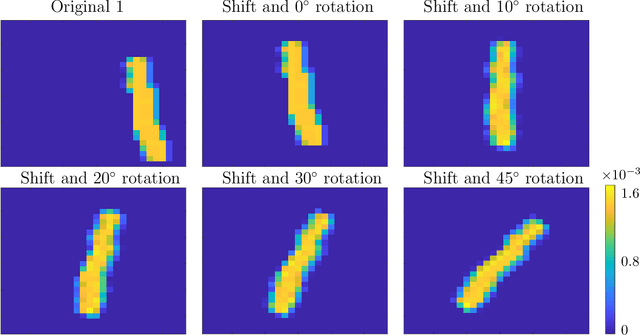
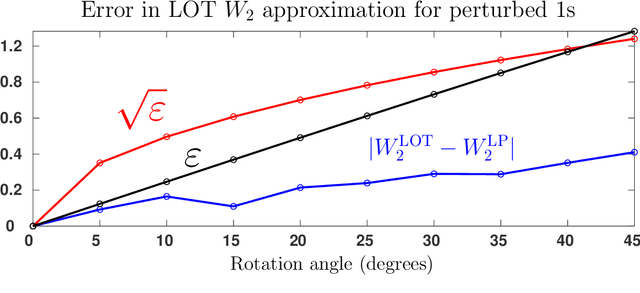
Discriminating between distributions is an important problem in a number of scientific fields. This motivated the introduction of Linear Optimal Transportation (LOT), which embeds the space of distributions into an $L^2$-space. The transform is defined by computing the optimal transport of each distribution to a fixed reference distribution, and has a number of benefits when it comes to speed of computation and to determining classification boundaries. In this paper, we characterize a number of settings in which LOT embeds families of distributions into a space in which they are linearly separable. This is true in arbitrary dimension, and for families of distributions generated through perturbations of shifts and scalings of a fixed distribution. We also prove conditions under which the $L^2$ distance of the LOT embedding between two distributions in arbitrary dimension is nearly isometric to Wasserstein-2 distance between those distributions. This is of significant computational benefit, as one must only compute $N$ optimal transport maps to define the $N^2$ pairwise distances between $N$ distributions. We demonstrate the benefits of LOT on a number of distribution classification problems.