Active Axial Motion Compensation in Multiphoton-Excited Fluorescence Microscopy

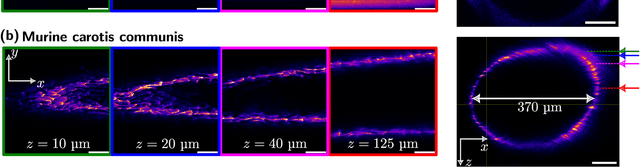
In living organisms, the natural motion caused by the heartbeat, breathing, or muscle movements leads to the deformation of tissue caused by translation and stretching of the tissue structure. This effect results in the displacement or deformation of the plane of observation for intravital microscopy and causes motion-induced aberrations of the resulting image data. This, in turn, places severe limitations on the time during which specific events can be observed in intravital imaging experiments. These limitations can be overcome if the tissue motion can be compensated such that the plane of observation remains steady. We have developed a mathematical shape space model that can predict the periodic motion of a cylindrical tissue phantom resembling blood vessels. This model is then used to rapidly calculate the future position of the plane of observation of a confocal multiphoton fluorescence microscope. The focal plane is continuously adjusted to the calculated position with a piezo-actuated objective lens holder. We demonstrate active motion compensation for non-harmonic axial displacements of the vessel phantom with a field of view up to 400 $\mu$m $\times$ 400 $\mu$m, vertical amplitudes of more than 100 $\mu$m, and at a rate of 0.5 Hz.

Parametrizing Product Shape Manifolds by Composite Networks

Parametrizations of data manifolds in shape spaces can be computed using the rich toolbox of Riemannian geometry. This, however, often comes with high computational costs, which raises the question if one can learn an efficient neural network approximation. We show that this is indeed possible for shape spaces with a special product structure, namely those smoothly approximable by a direct sum of low-dimensional manifolds. Our proposed architecture leverages this structure by separately learning approximations for the low-dimensional factors and a subsequent combination. After developing the approach as a general framework, we apply it to a shape space of triangular surfaces. Here, typical examples of data manifolds are given through datasets of articulated models and can be factorized, for example, by a Sparse Principal Geodesic Analysis (SPGA). We demonstrate the effectiveness of our proposed approach with experiments on synthetic data as well as manifolds extracted from data via SPGA.

Learning Low Bending and Low Distortion Manifold Embeddings: Theory and Applications

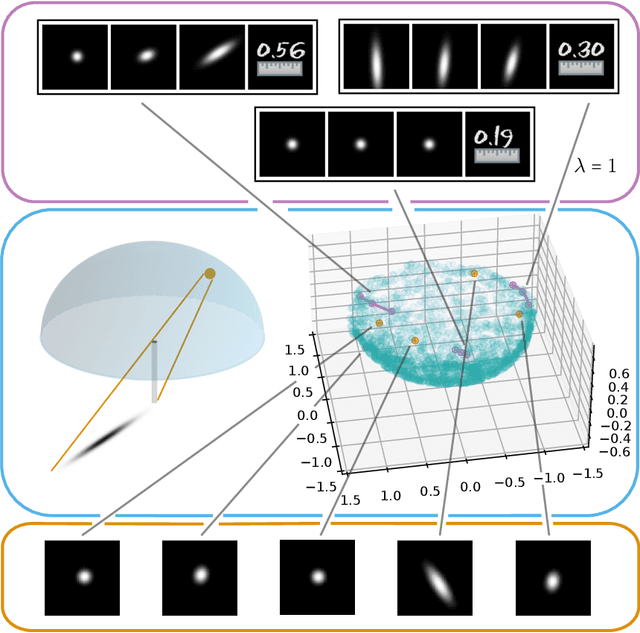
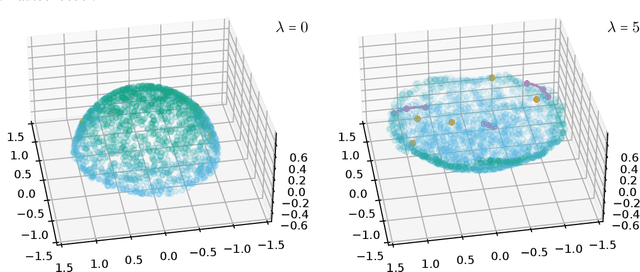
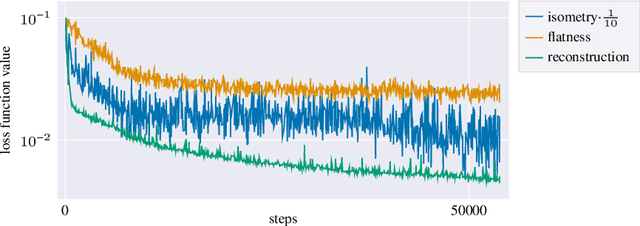
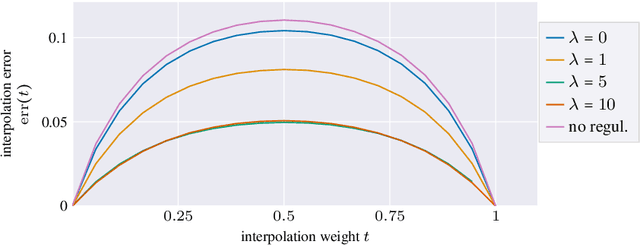
Autoencoders, which consist of an encoder and a decoder, are widely used in machine learning for dimension reduction of high-dimensional data. The encoder embeds the input data manifold into a lower-dimensional latent space, while the decoder represents the inverse map, providing a parametrization of the data manifold by the manifold in latent space. A good regularity and structure of the embedded manifold may substantially simplify further data processing tasks such as cluster analysis or data interpolation. We propose and analyze a novel regularization for learning the encoder component of an autoencoder: a loss functional that prefers isometric, extrinsically flat embeddings and allows to train the encoder on its own. To perform the training it is assumed that for pairs of nearby points on the input manifold their local Riemannian distance and their local Riemannian average can be evaluated. The loss functional is computed via Monte Carlo integration with different sampling strategies for pairs of points on the input manifold. Our main theorem identifies a geometric loss functional of the embedding map as the $\Gamma$-limit of the sampling-dependent loss functionals. Numerical tests, using image data that encodes different explicitly given data manifolds, show that smooth manifold embeddings into latent space are obtained. Due to the promotion of extrinsic flatness, these embeddings are regular enough such that interpolation between not too distant points on the manifold is well approximated by linear interpolation in latent space as one possible postprocessing.

Learning low bending and low distortion manifold embeddings

Autoencoders are a widespread tool in machine learning to transform high-dimensional data into a lowerdimensional representation which still exhibits the essential characteristics of the input. The encoder provides an embedding from the input data manifold into a latent space which may then be used for further processing. For instance, learning interpolation on the manifold may be simplified via the new manifold representation in latent space. The efficiency of such further processing heavily depends on the regularity and structure of the embedding. In this article, the embedding into latent space is regularized via a loss function that promotes an as isometric and as flat embedding as possible. The required training data comprises pairs of nearby points on the input manifold together with their local distance and their local Frechet average. This regularity loss functional even allows to train the encoder on its own. The loss functional is computed via a Monte Carlo integration which is shown to be consistent with a geometric loss functional defined directly on the embedding map. Numerical tests are performed using image data that encodes different data manifolds. The results show that smooth manifold embeddings in latent space are obtained. These embeddings are regular enough such that interpolation between not too distant points on the manifold is well approximated by linear interpolation in latent space.

Dynamic Cell Imaging in PET with Optimal Transport Regularization

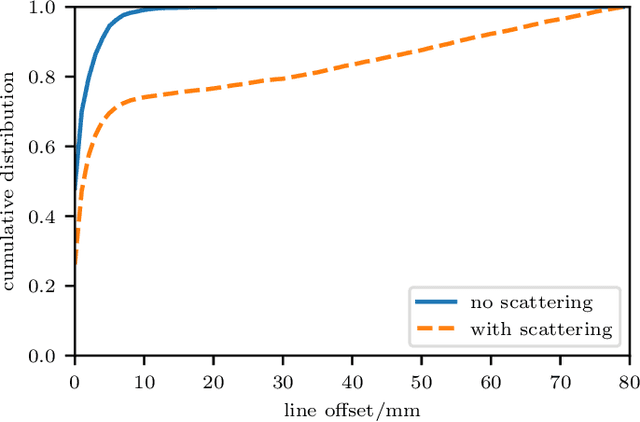
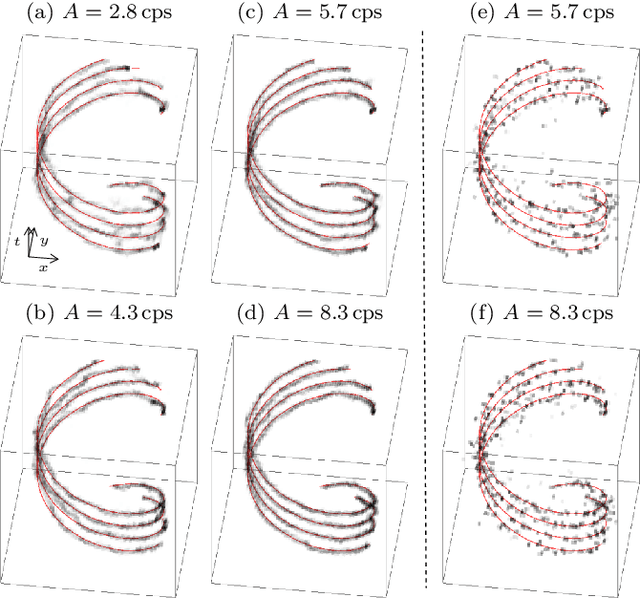
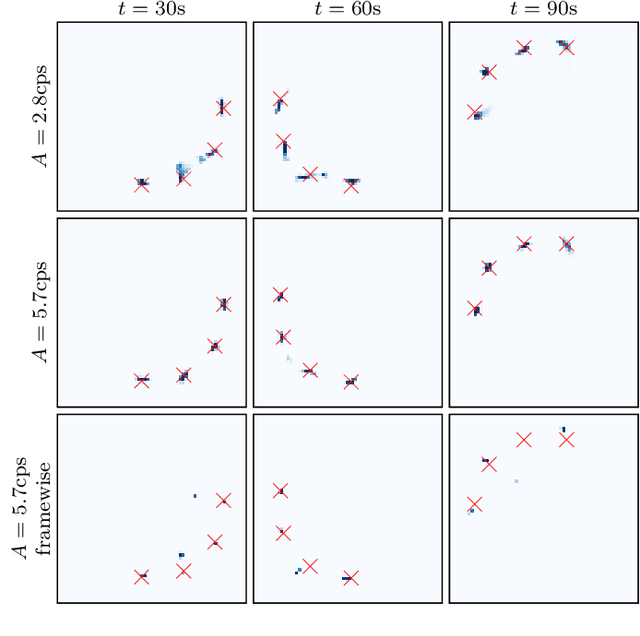
We propose a novel dynamic image reconstruction method from PET listmode data that could be particularly suited to tracking single or small numbers of cells. In contrast to conventional PET reconstruction the proposed method combines the information from all detected events not only to reconstruct the dynamic evolution of the radionuclide distribution, but also to simultaneously improve the reconstruction at each single time point by enforcing temporal consistency. This is achieved via the use of optimal transport regularization where in principle, among all possible temporally evolving radionuclide distributions consistent with the PET measurement, the one is chosen with least kinetic motion energy. The reconstruction is found by convex optimization so that there is no dependence on the initialization of the method. We study its behaviour on simulated data of a human PET system and demonstrate its robustness even in settings with very low radioactivity. In contrast to previously reported cell tracking algorithms, the proposed technique is oblivious to the number of tracked cells. Without any additional complexity one or multiple cells can be reconstructed, and the model automatically determines the number of particles. As one of the results, four radiolabelled cells moving with a velocity of 3.1 mm/s and a PET recorded count rate of 1.1 cps (for each cell) could be simultaneously tracked with a tracking accuracy of 5.4 mm inside a simulated human body.

A Framework for Wasserstein-1-Type Metrics

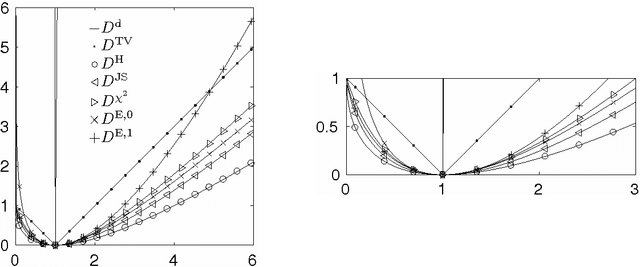
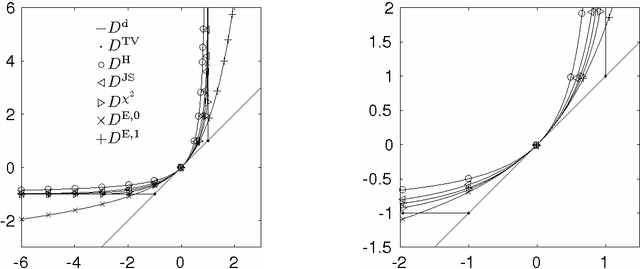
We propose a unifying framework for generalising the Wasserstein-1 metric to a discrepancy measure between nonnegative measures of different mass. This generalization inherits the convexity and computational efficiency from the Wasserstein-1 metric, and it includes several previous approaches from the literature as special cases. For various specific instances of the generalized Wasserstein-1 metric we furthermore demonstrate their usefulness in applications by numerical experiments.

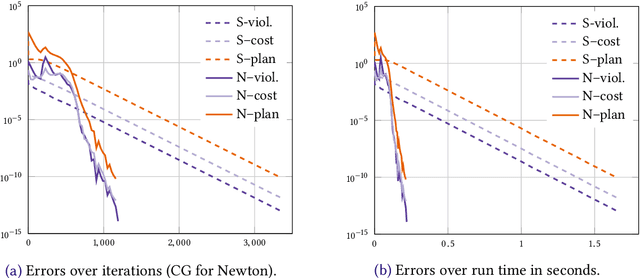
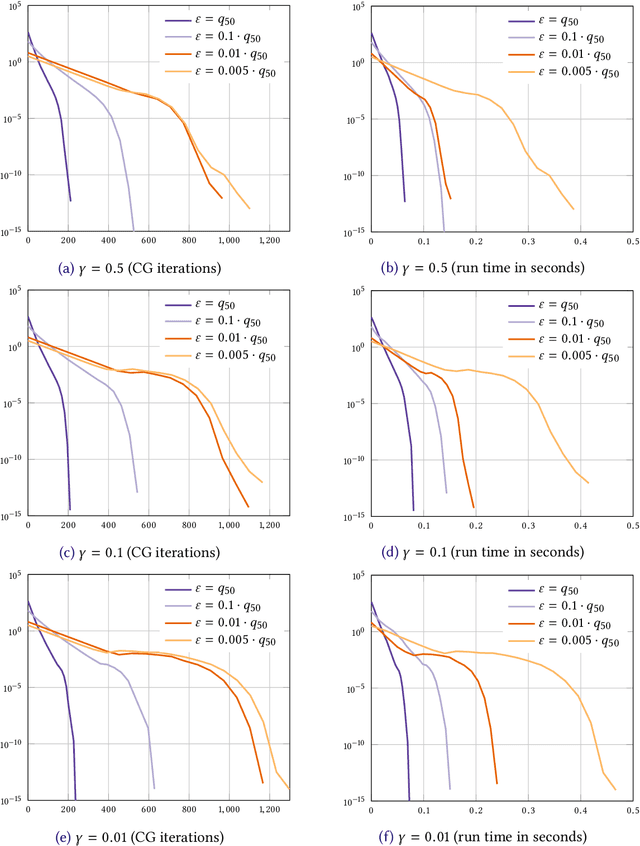
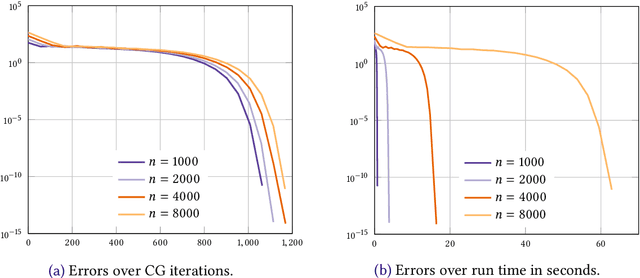
A Sinkhorn-Newton method for entropic optimal transport

We consider the entropic regularization of discretized optimal transport and propose to solve its optimality conditions via a logarithmic Newton iteration. We show a quadratic convergence rate and validate numerically that the method compares favorably with the more commonly used Sinkhorn--Knopp algorithm for small regularization strength. We further investigate numerically the robustness of the proposed method with respect to parameters such as the mesh size of the discretization.

Joint denoising and distortion correction of atomic scale scanning transmission electron microscopy images

Nowadays, modern electron microscopes deliver images at atomic scale. The precise atomic structure encodes information about material properties. Thus, an important ingredient in the image analysis is to locate the centers of the atoms shown in micrographs as precisely as possible. Here, we consider scanning transmission electron microscopy (STEM), which acquires data in a rastering pattern, pixel by pixel. Due to this rastering combined with the magnification to atomic scale, movements of the specimen even at the nanometer scale lead to random image distortions that make precise atom localization difficult. Given a series of STEM images, we derive a Bayesian method that jointly estimates the distortion in each image and reconstructs the underlying atomic grid of the material by fitting the atom bumps with suitable bump functions. The resulting highly non-convex minimization problems are solved numerically with a trust region approach. Well-posedness of the reconstruction method and the model behavior for faster and faster rastering are investigated using variational techniques. The performance of the method is finally evaluated on both synthetic and real experimental data.

Discrete geodesic calculus in the space of viscous fluidic objects

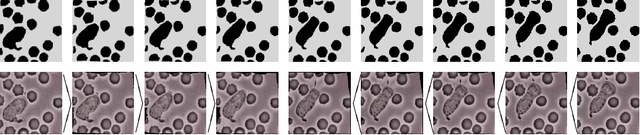
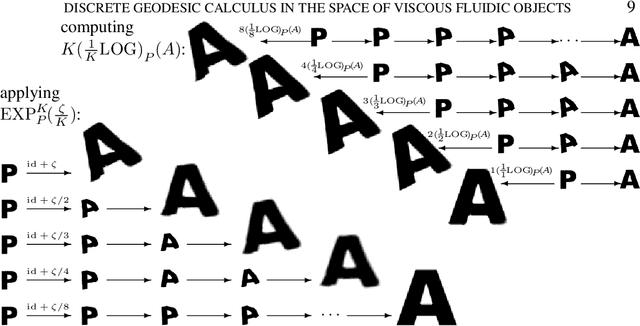
Based on a local approximation of the Riemannian distance on a manifold by a computationally cheap dissimilarity measure, a time discrete geodesic calculus is developed, and applications to shape space are explored. The dissimilarity measure is derived from a deformation energy whose Hessian reproduces the underlying Riemannian metric, and it is used to define length and energy of discrete paths in shape space. The notion of discrete geodesics defined as energy minimizing paths gives rise to a discrete logarithmic map, a variational definition of a discrete exponential map, and a time discrete parallel transport. This new concept is applied to a shape space in which shapes are considered as boundary contours of physical objects consisting of viscous material. The flexibility and computational efficiency of the approach is demonstrated for topology preserving shape morphing, the representation of paths in shape space via local shape variations as path generators, shape extrapolation via discrete geodesic flow, and the transfer of geometric features.